2.9 Cos 17
stanleys
Sep 16, 2025 · 6 min read
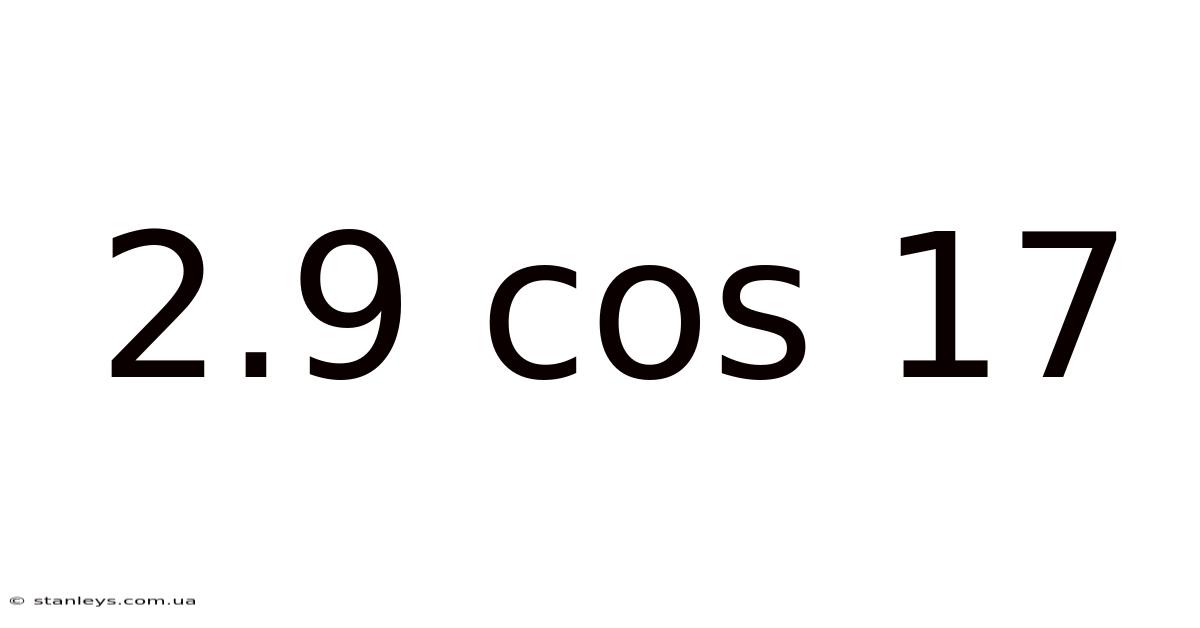
Table of Contents
Decoding 2.9 cos 17: A Deep Dive into Trigonometric Calculations
This article delves into the intricacies of calculating 2.9 cos 17, explaining the underlying trigonometric principles, the steps involved, and the practical applications of such calculations. Understanding this seemingly simple expression requires a grasp of fundamental trigonometry, the use of calculators or software, and an awareness of potential errors and limitations. We'll explore the process thoroughly, providing a clear and comprehensive guide suitable for students and anyone interested in strengthening their mathematical skills. The keywords we'll focus on include: trigonometry, cosine, radians versus degrees, calculator usage, significant figures, approximation, and practical applications.
Understanding the Basics: Trigonometry and Cosine
Before tackling 2.9 cos 17, let's review the fundamentals. Trigonometry, at its core, is the study of the relationships between angles and sides of triangles. It's a crucial branch of mathematics used extensively in physics, engineering, computer graphics, and many other fields.
The cosine function (cos) is one of the three primary trigonometric functions (along with sine and tangent). In a right-angled triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse.
- cos θ = Adjacent / Hypotenuse
where θ (theta) represents the angle.
However, the cosine function's application extends beyond right-angled triangles. It's a periodic function, meaning its values repeat over a certain interval (2π radians or 360 degrees). This cyclical nature makes it invaluable for modeling periodic phenomena, such as oscillations and waves.
The Significance of Units: Degrees vs. Radians
A critical aspect of trigonometric calculations is understanding the units used to measure angles. Two common units are:
- Degrees: A full circle is divided into 360 degrees (360°).
- Radians: A full circle is divided into 2π radians (approximately 6.28 radians). Radians are often preferred in advanced mathematics and physics because they simplify many formulas and calculations.
In the expression 2.9 cos 17, we need to clarify whether 17 represents 17 degrees or 17 radians. Unless otherwise specified, it's generally assumed that the angle is in degrees. Therefore, we'll proceed with the calculation assuming 17 degrees.
Calculating 2.9 cos 17°: A Step-by-Step Guide
Calculating 2.9 cos 17° involves two main steps:
-
Finding the cosine of 17°: This requires a scientific calculator or mathematical software. Most calculators have a "cos" button. Simply enter 17, ensure your calculator is set to degrees mode (not radians), and press the "cos" button. The result will be a decimal approximation of cos 17°.
-
Multiplying by 2.9: Once you have the value of cos 17°, multiply this value by 2.9. This gives you the final answer.
Let's assume that your calculator gives you cos 17° ≈ 0.9563. (Note: this value is an approximation; the actual value has infinitely many decimal places).
Then:
2.9 * 0.9563 ≈ 2.773
Therefore, 2.9 cos 17° ≈ 2.773
Important Note: The precision of your result depends on the precision of your calculator and the number of significant figures you choose to retain. Using more significant figures in the intermediate steps will generally lead to a more accurate final answer.
Understanding the Approximation and Significant Figures
It's crucial to understand that the value we calculated, 2.773, is an approximation. The cosine function, when evaluated at most angles, produces irrational numbers—numbers with infinitely many non-repeating decimal places. Our calculators provide truncated approximations to a certain number of decimal places.
The concept of significant figures helps us manage the uncertainty associated with approximations. Significant figures indicate the number of digits that are reliably known in a measurement or calculation. In our example, we might choose to report the answer as 2.77, using three significant figures, reflecting the limitations of our calculator's precision and the inherent approximation in the cosine function.
Exploring the Calculation with Radians
If, hypothetically, 17 represented 17 radians, the calculation would be significantly different. 17 radians is considerably more than one full circle (2π ≈ 6.28 radians). To calculate cos(17 radians), you would again use a calculator, but ensure it's set to radians mode. The result will be a different decimal value, and subsequently, multiplying by 2.9 will yield a different final answer. The calculator should give a value close to -0.353. Therefore, 2.9 cos(17 radians) ≈ -1.024. Always pay close attention to the angular unit.
Practical Applications: Where is this used?
Calculations like 2.9 cos 17° appear frequently in various fields. Some examples include:
-
Physics: Modeling simple harmonic motion (e.g., a pendulum's swing), analyzing wave phenomena (sound, light), and solving problems involving vectors and forces.
-
Engineering: Designing structures, analyzing stresses and strains, and calculating trajectories of projectiles.
-
Computer Graphics: Creating realistic animations and simulations, rendering 3D objects, and implementing lighting and shading effects.
-
Navigation: Determining distances and positions using triangulation and other techniques.
Frequently Asked Questions (FAQ)
Q1: Why is the cosine value always between -1 and 1?
A1: The cosine function, geometrically interpreted as the ratio of adjacent side to the hypotenuse in a right-angled triangle, can never exceed 1 (since the hypotenuse is always the longest side). The negative values arise when the angle lies in the second or third quadrants of the unit circle, where the x-coordinate (which represents the cosine) is negative.
Q2: What if I don't have a scientific calculator?
A2: You can use online calculators or mathematical software like MATLAB, Python (with libraries like NumPy), or Wolfram Alpha. These tools provide precise calculations and handle radians and degrees appropriately.
Q3: How can I improve the accuracy of my calculations?
A3: Use a calculator or software with high precision (more decimal places). Also, consider using more significant figures during intermediate steps before rounding off the final answer.
Q4: What are the limitations of using a calculator for trigonometric functions?
A4: Calculators provide approximations of trigonometric functions, not exact values. The precision is limited by the internal representation of numbers within the calculator.
Conclusion: Mastering Trigonometric Calculations
The seemingly simple calculation of 2.9 cos 17° reveals the depth and intricacies involved in trigonometry. Understanding the fundamental concepts, the units used for angles, and the limitations of approximations is crucial for accurate and meaningful calculations. Mastering these principles is essential for anyone working with mathematics and its applications in various scientific and engineering fields. Remember to always pay attention to the units (degrees or radians) and use appropriate tools (calculators or software) for accurate results. With practice and a clear understanding of the underlying principles, you can confidently tackle more complex trigonometric problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2.9 Cos 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.