X 3 9
stanleys
Sep 11, 2025 · 6 min read
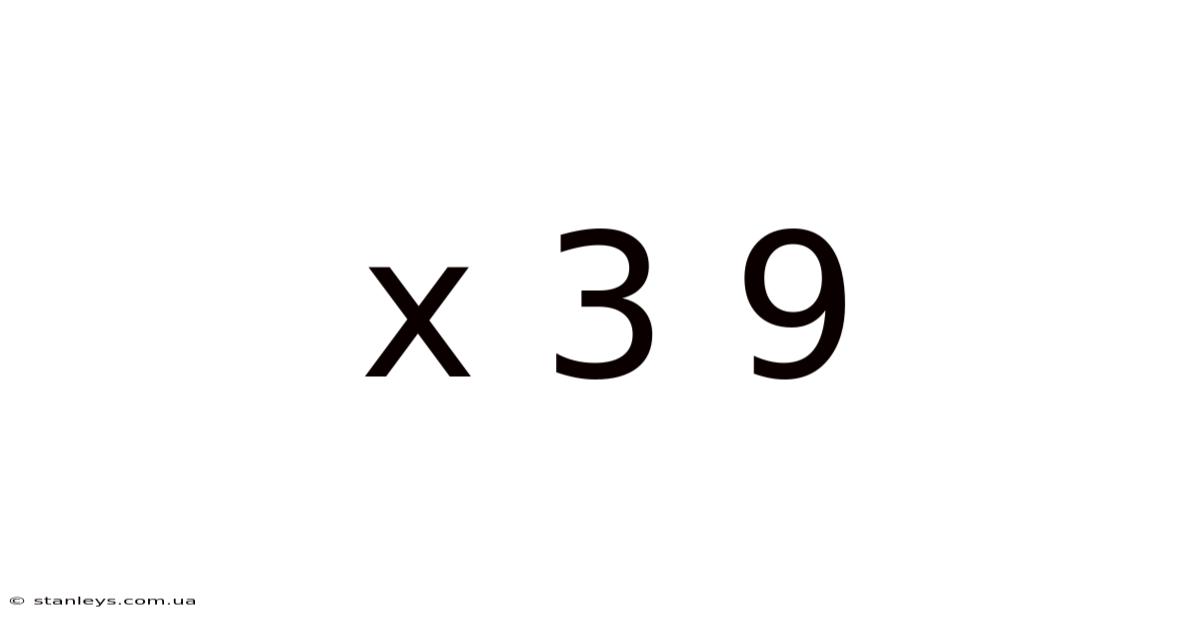
Table of Contents
Unlocking the Mysteries of X³ + 9: A Deep Dive into Cubic Equations and Beyond
The seemingly simple expression "x³ + 9" might appear innocuous at first glance. However, it opens the door to a fascinating exploration of cubic equations, their solutions, complex numbers, and the broader world of algebra. This article will delve into the intricacies of this expression, exploring its properties, solving methods, and implications within a wider mathematical context. We will also touch upon related concepts and applications, ensuring a comprehensive understanding suitable for students and enthusiasts alike.
Introduction: Understanding Cubic Equations
A cubic equation is a polynomial equation of the third degree, meaning the highest power of the variable (x in this case) is 3. The general form of a cubic equation is ax³ + bx² + cx + d = 0, where a, b, c, and d are constants, and a ≠ 0. Our focus, x³ + 9 = 0, is a simplified version of this general form, where b = c = 0 and d = -9. This specific equation lacks a quadratic and linear term, making it a relatively simpler case to analyze, yet still rich with educational value. Understanding its solution provides a solid foundation for tackling more complex cubic equations. This seemingly simple equation provides a springboard for understanding more advanced concepts in algebra and number theory.
Solving x³ + 9 = 0: A Step-by-Step Approach
To solve x³ + 9 = 0, we need to isolate x. The first step is straightforward:
-
Isolate x³: Subtract 9 from both sides of the equation: x³ = -9
-
Find the Cube Root: To find the value of x, we take the cube root of both sides: x = ∛(-9)
This might seem like the final answer, but it's crucial to understand the nuances of cube roots, especially when dealing with negative numbers. The cube root of a negative number is also a negative number. However, the story doesn't end there. The complex number system plays a significant role in finding all possible solutions.
The Role of Complex Numbers
While the real cube root of -9 is approximately -2.08, there are two other complex cube roots. To understand this, we need to introduce the concept of complex numbers. Complex numbers are numbers of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (√-1).
The equation x³ = -9 can be solved using polar form and De Moivre's Theorem. We can represent -9 in polar form as 9(cos(π) + i sin(π)). According to De Moivre's Theorem, the cube roots are given by:
xₖ = ∛9 [cos((π + 2kπ)/3) + i sin((π + 2kπ)/3)], where k = 0, 1, 2.
Let's calculate the three roots:
- k = 0: x₀ = ∛9 [cos(π/3) + i sin(π/3)] ≈ 1.04 + 1.80i
- k = 1: x₁ = ∛9 [cos(π) + i sin(π)] ≈ -2.08
- k = 2: x₂ = ∛9 [cos(5π/3) + i sin(5π/3)] ≈ 1.04 - 1.80i
Therefore, the equation x³ + 9 = 0 has three solutions: one real solution (approximately -2.08) and two complex conjugate solutions (approximately 1.04 + 1.80i and 1.04 - 1.80i). This demonstrates a fundamental property of cubic equations: they always have three roots, which may be real or complex.
Graphical Representation and Visualizing the Roots
The solutions can be visually represented on the complex plane (also known as the Argand plane). The real solution lies on the negative real axis, while the complex solutions are symmetrically placed in the complex plane. This visual representation enhances understanding by providing a geometric interpretation of the algebraic solutions.
Expanding the Understanding: Beyond x³ + 9 = 0
The analysis of x³ + 9 = 0 provides a solid foundation for tackling more complex cubic equations. By understanding the methodology employed in solving this simplified equation, one can develop the skills needed to solve cubic equations with all three terms (ax³ + bx² + cx + d = 0). These more general cubic equations can be solved using various methods, including:
- Factoring: If the cubic equation can be factored, it simplifies the process of finding the roots.
- Cardano's Method: This algebraic method provides a formula for solving cubic equations, albeit a somewhat complex one.
- Numerical Methods: For cubic equations that cannot be solved easily using algebraic methods, numerical methods (like the Newton-Raphson method) provide approximate solutions.
Applications of Cubic Equations
Cubic equations find application in diverse fields:
- Engineering: Designing structures, analyzing fluid flow, and solving problems in thermodynamics often involve cubic equations.
- Physics: Calculating trajectories, modelling oscillations, and understanding various physical phenomena require the use of cubic equations.
- Chemistry: Equilibrium calculations and reaction kinetics sometimes involve cubic equations.
- Economics: Modeling certain economic scenarios can require the use of cubic equations.
Frequently Asked Questions (FAQ)
-
Q: Why are complex numbers necessary to solve x³ + 9 = 0?
- A: Because the cube root of a negative number involves the imaginary unit 'i', complex numbers are needed to express all three roots of the cubic equation completely. The real number system alone is insufficient to represent all solutions.
-
Q: Are there other methods to solve x³ + 9 = 0 besides the cube root and De Moivre's Theorem?
- A: While the methods used above are efficient, numerical methods could also provide approximate solutions, especially useful when dealing with more complex cubic equations.
-
Q: What if the equation were x³ - 9 = 0? How would the solution differ?
- A: The solution would involve finding the cube root of 9. There would still be three roots, but one would be real and positive, and the other two would be complex conjugates.
-
Q: How do I solve more complex cubic equations?
- A: For more complex cubic equations (ax³ + bx² + cx + d = 0), more advanced techniques like Cardano's method or numerical methods become necessary. These methods are beyond the scope of this article but are widely available in advanced algebra textbooks and online resources.
Conclusion: A Deeper Appreciation of Mathematics
The seemingly simple equation x³ + 9 = 0 has proven to be a gateway to a much richer understanding of cubic equations, complex numbers, and their applications. Solving this equation has demonstrated the power and beauty of mathematics, revealing a surprising depth within a concise algebraic expression. By exploring this example, we have not only solved a specific equation but also gained a deeper appreciation for the underlying mathematical principles and their broader relevance across various scientific and engineering disciplines. The journey through solving x³ + 9 = 0 highlights the interconnectedness of mathematical concepts and their ability to unveil the secrets hidden within seemingly simple expressions. The exploration of complex numbers in the context of this cubic equation serves as an excellent starting point for further mathematical explorations, prompting a more profound understanding of the mathematical world. Further research into related concepts like polynomial equations of higher degrees will build upon this foundation, leading to an even greater appreciation for the elegant power and practical utility of mathematics.
Latest Posts
Latest Posts
-
Buckle Up Buttercup
Sep 11, 2025
-
18cm In Feet
Sep 11, 2025
-
Lost To Antiquity
Sep 11, 2025
-
25 Of 1500
Sep 11, 2025
-
4242 Angel Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about X 3 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.