25 Of 1500
stanleys
Sep 11, 2025 · 5 min read
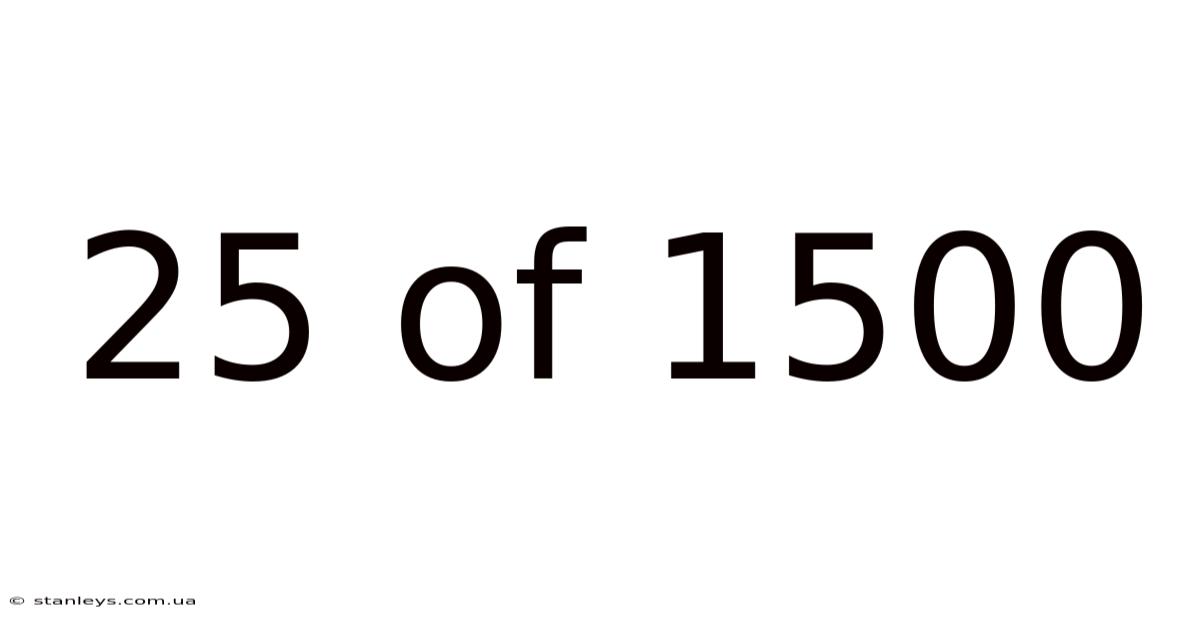
Table of Contents
Understanding the Fraction 25/1500: A Deep Dive into Simplification, Percentage, and Real-World Applications
The fraction 25/1500 might seem daunting at first glance, but understanding it unlocks a pathway to mastering fundamental mathematical concepts. This article will explore the simplification of this fraction, its equivalent percentage, and provide real-world examples to solidify your comprehension. We'll delve into the underlying principles, making this seemingly complex topic accessible and engaging for everyone, from students to curious adults.
I. Introduction: Why 25/1500 Matters
The fraction 25/1500 represents a part-to-whole relationship. It signifies 25 parts out of a total of 1500 parts. Understanding how to manipulate and interpret such fractions is crucial in various fields, including finance, statistics, and everyday problem-solving. This comprehensive guide aims to demystify this specific fraction and illuminate the broader concepts it embodies. We'll cover simplification, conversion to percentage, and practical applications, ensuring a thorough and insightful understanding. Learning to work with fractions like 25/1500 builds a strong foundation for more advanced mathematical concepts.
II. Simplifying 25/1500: Finding the Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its lowest terms. This is achieved by finding the greatest common divisor (GCD) of the numerator (25) and the denominator (1500). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's find the GCD of 25 and 1500. We can use the prime factorization method:
- Prime factorization of 25: 5 x 5 = 5²
- Prime factorization of 1500: 2 x 2 x 3 x 5 x 5 x 5 = 2² x 3 x 5³
The common factors are 5 x 5 = 25. Therefore, the GCD of 25 and 1500 is 25.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
25/1500 = (25 ÷ 25) / (1500 ÷ 25) = 1/60
Therefore, the simplified form of 25/1500 is 1/60. This simplified fraction is much easier to work with and understand.
III. Converting 1/60 to a Percentage
Converting a fraction to a percentage is a fundamental skill. To convert 1/60 to a percentage, we perform the following calculation:
(1/60) x 100% = 1.666...%
This can be rounded to 1.67%. This means that 25 out of 1500 represents approximately 1.67% of the whole.
IV. Real-World Applications of 25/1500 and its Simplified Form 1/60
Understanding fractions like 25/1500 and its simplified equivalent, 1/60, has numerous practical applications:
-
Finance: Imagine you invested $1500 and earned a profit of $25. The fraction 25/1500 (or 1/60) represents your return on investment. Converting this to a percentage (1.67%) provides a clear picture of your investment's performance.
-
Statistics: Suppose a survey of 1500 people revealed that 25 preferred a particular product. The fraction 25/1500 (or 1.67%) shows the proportion of people who prefer that product. This data is crucial for market research and product development.
-
Test Scores: If a test had 1500 possible points, and a student scored 25 points, their score is represented by 25/1500, or 1/60, which is approximately 1.67%. This gives a clear representation of their performance relative to the maximum possible score.
-
Manufacturing: If a factory produces 1500 items and 25 are defective, the fraction 25/1500 (or 1/60, approximately 1.67%) indicates the defect rate. This information is vital for quality control and process improvement.
-
Surveys and Polls: If a poll of 1500 voters shows that 25 support a particular candidate, the fraction 25/1500 (or 1.67%) represents the candidate's level of support within that specific sample. This information is critical in election forecasting and political analysis.
V. Further Exploration: Working with Fractions
While we've focused on 25/1500, the principles discussed apply to other fractions. Mastering fraction simplification and percentage conversion is fundamental to many mathematical concepts:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. Simplifying fractions before performing these operations often makes the calculation easier.
-
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators and the denominators separately. Dividing fractions is equivalent to multiplying by the reciprocal of the divisor.
-
Ratios and Proportions: Fractions are directly related to ratios and proportions, which are used extensively in various fields.
-
Decimals: Fractions can be easily converted to decimals, and vice-versa. This allows for flexibility when performing calculations.
-
Algebra: Fractions are an integral part of algebraic equations and manipulations.
VI. Understanding the Concept of Proportions
The fraction 25/1500 is a representation of a proportion. A proportion is a statement that two ratios are equal. We can express the proportion as:
25/1500 = x/100 (where x is the percentage)
Solving for x, we get:
x = (25/1500) * 100 = 1.67%
VII. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 25/1500?
- A: The simplest form is 1/60.
-
Q: How do I convert 25/1500 to a percentage?
- A: Divide the numerator by the denominator and multiply by 100%. (25/1500) x 100% ≈ 1.67%
-
Q: What is the greatest common divisor (GCD) of 25 and 1500?
- A: The GCD is 25.
-
Q: Are there other ways to simplify 25/1500 besides using the GCD?
- A: Yes, you can simplify iteratively by dividing both the numerator and denominator by common factors until you reach the simplest form. For example, you could divide both by 5 to get 5/300, then by 5 again to get 1/60.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It's essential for clear communication and accurate problem-solving.
VIII. Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions like 25/1500 is more than just memorizing procedures; it's about grasping the fundamental concepts of ratios, proportions, and percentages. These concepts are applied across numerous fields, from finance and statistics to engineering and everyday life. By mastering simplification and conversion techniques, you build a solid foundation for more advanced mathematical studies and problem-solving skills. The seemingly simple fraction 25/1500 serves as a powerful gateway to understanding these critical concepts and unlocking your mathematical potential. Continue practicing with different fractions, and you'll find that working with them becomes increasingly intuitive and rewarding.
Latest Posts
Latest Posts
-
197lbs In Kg
Sep 11, 2025
-
63 5kg In Lbs
Sep 11, 2025
-
47 3kg In Stone
Sep 11, 2025
-
20 Of 350000
Sep 11, 2025
-
1 3 Of 90
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 1500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.