X 2 8
stanleys
Sep 11, 2025 · 6 min read
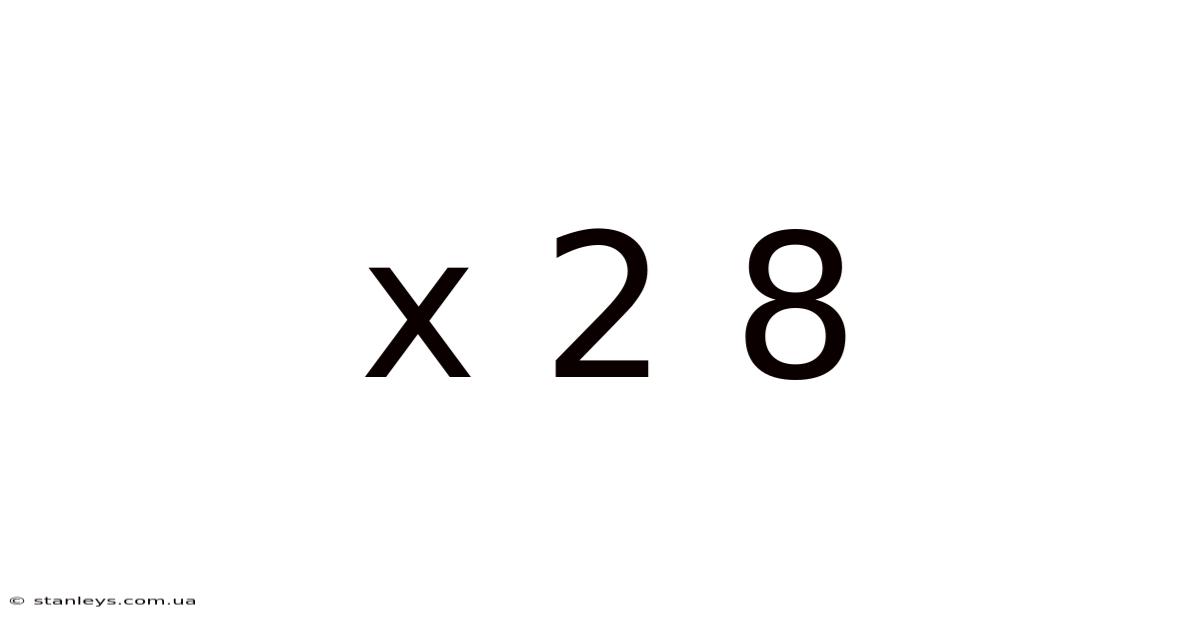
Table of Contents
Decoding X² + 8: A Comprehensive Exploration of Quadratic Expressions
Understanding quadratic expressions is fundamental to mastering algebra and its numerous applications in various fields, from physics and engineering to economics and computer science. This article delves into the specific quadratic expression x² + 8, exploring its properties, potential manipulations, and broader relevance within the realm of mathematics. We'll go beyond a simple definition, examining its graphical representation, solving related equations, and highlighting its role in more complex mathematical concepts.
Introduction: Unveiling the Basics of x² + 8
The expression x² + 8 is a quadratic expression because the highest power of the variable 'x' is 2. It's a simple form of a quadratic, lacking a linear (x) term and having a constant term of 8. This seemingly straightforward expression provides a valuable foundation for understanding more complex quadratic equations and functions. This article aims to demystify this fundamental building block, explaining its characteristics and demonstrating how to approach related problems. We will explore how to solve equations involving this expression, analyze its graphical representation, and even touch upon its applications in higher-level mathematics.
Analyzing the Structure: Components of a Quadratic Expression
Before we delve into solving equations or graphing the expression, let's break down its components:
-
x²: This term represents the squared variable. It dictates the parabolic shape of the quadratic function when graphed. The coefficient of x² (in this case, 1) determines the parabola's concavity (opens upwards if positive, downwards if negative).
-
8: This is the constant term. It represents the y-intercept of the graph; the point where the parabola intersects the y-axis. In this case, the parabola intersects the y-axis at the point (0, 8).
-
Lack of a linear term: The absence of an 'x' term (a term like 3x or -2x) simplifies the expression but also limits certain properties. We will see how this affects the symmetry and vertex of the parabola.
Graphical Representation: Visualizing x² + 8
To visualize x² + 8, we can create a graph by plotting points. We can choose various values of 'x' and calculate the corresponding values of x² + 8:
| x | x² | x² + 8 |
|---|---|---|
| -3 | 9 | 17 |
| -2 | 4 | 12 |
| -1 | 1 | 9 |
| 0 | 0 | 8 |
| 1 | 1 | 9 |
| 2 | 4 | 12 |
| 3 | 9 | 17 |
Plotting these points will reveal a parabola that opens upwards, symmetrical around the y-axis, with its vertex at (0, 8). The parabola extends infinitely in both directions. The absence of a linear term results in this symmetrical shape, with the vertex lying directly on the y-axis. This simple graph demonstrates the visual representation of this specific quadratic expression.
Solving Equations Involving x² + 8
While x² + 8 itself isn't an equation (it lacks an equals sign), we can construct equations using this expression. Let's examine a few examples:
1. x² + 8 = 0: This equation asks us to find the values of 'x' that make the expression equal to zero. Solving this involves subtracting 8 from both sides: x² = -8. Taking the square root of both sides introduces imaginary numbers, as the square root of a negative number is not a real number. The solutions are x = ±√(-8) = ±2i√2, where 'i' represents the imaginary unit (√-1).
2. x² + 8 = 17: Subtracting 17 from both sides gives x² = 9. Taking the square root yields x = ±3. This demonstrates that there can be two real solutions to a quadratic equation.
3. x² + 8 = k (where k is a constant): This general form allows us to explore solutions for different values of 'k'. Solving for 'x' results in x = ±√(k - 8). The existence of real solutions depends on the value of 'k'. If k < 8, the solutions will be imaginary; if k ≥ 8, the solutions will be real.
Completing the Square and the Vertex Form
While x² + 8 is already in a relatively simple form, we can still apply mathematical techniques to gain further insights. Completing the square is a useful method for transforming quadratic expressions into a form that reveals the vertex of the parabola. However, in the case of x² + 8, completing the square doesn't alter the expression significantly, as there's no linear term to manipulate. The vertex form of a quadratic is given by a(x - h)² + k, where (h, k) represents the vertex. For x² + 8, the vertex form is simply 1(x - 0)² + 8, confirming the vertex at (0, 8).
Applications in Calculus and Beyond
The expression x² + 8, while simple, acts as a fundamental building block in more complex mathematical concepts. In calculus, its derivative (2x) represents the slope of the tangent line at any point on the parabola. The second derivative (2) confirms the parabola's constant concavity. Furthermore, this basic quadratic can be used to represent simpler parabolic models in various fields, such as the trajectory of a projectile under specific conditions (ignoring air resistance), or basic optimization problems in economics.
Extending the Concept: Variations and Generalizations
The simplicity of x² + 8 allows us to explore more complex quadratic expressions by adding a linear term (ax + b). The general form of a quadratic equation is ax² + bx + c = 0. By varying the coefficients 'a', 'b', and 'c', we can generate countless quadratic expressions, each with its own unique properties and graphical representation. Understanding the behavior of x² + 8 provides a strong foundation for understanding these more complex variations.
Frequently Asked Questions (FAQs)
Q1: What is the discriminant of x² + 8 = 0?
A1: The discriminant (b² - 4ac) is used to determine the nature of the roots of a quadratic equation (ax² + bx + c = 0). In x² + 8 = 0, a = 1, b = 0, and c = 8. Therefore, the discriminant is 0² - 4(1)(8) = -32. A negative discriminant indicates that the roots are complex conjugates (imaginary).
Q2: Can x² + 8 be factored?
A2: Over the real numbers, x² + 8 cannot be factored. However, using complex numbers, it can be factored as (x + 2i√2)(x - 2i√2).
Q3: What is the axis of symmetry of the parabola represented by x² + 8?
A3: The axis of symmetry is the vertical line that divides the parabola into two mirror images. For x² + 8, the axis of symmetry is x = 0 (the y-axis).
Q4: How does the constant term '8' affect the graph?
A4: The constant term '8' determines the y-intercept of the parabola. It shifts the entire parabola vertically upwards by 8 units compared to a basic parabola like y = x².
Conclusion: A Foundation for Further Exploration
x² + 8, though seemingly a simple expression, offers a rich opportunity to understand the fundamental concepts of quadratic functions and equations. Its analysis provides a stepping stone to mastering more complex quadratic expressions and their applications across various mathematical and scientific fields. Through examining its graphical representation, solving related equations, and understanding its role in calculus, we've uncovered its significance in a broader mathematical context. This foundational knowledge paves the way for deeper exploration of more intricate mathematical concepts. This detailed analysis should equip you with a stronger understanding of quadratic expressions and the power of mathematical analysis.
Latest Posts
Latest Posts
-
Dl In Liter
Sep 11, 2025
-
57 9kg In Stone
Sep 11, 2025
-
Blue Pink Colour
Sep 11, 2025
-
Standard Deviation Graph
Sep 11, 2025
-
Sports Marketing Positions
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about X 2 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.