X 2 17
stanleys
Sep 14, 2025 · 7 min read
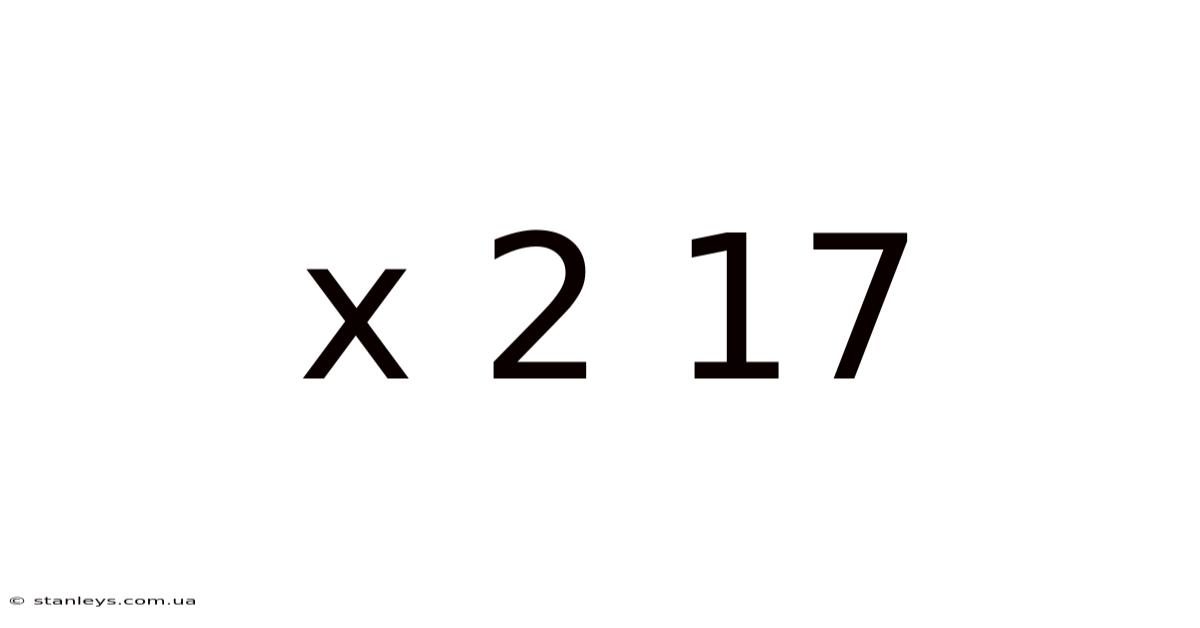
Table of Contents
Unraveling the Mystery: Exploring the Significance of x² + 17
The expression x² + 17 might seem deceptively simple at first glance. Just a few symbols – a variable, an exponent, a plus sign, and a constant. However, this seemingly straightforward algebraic expression opens doors to a fascinating exploration of number theory, quadratic equations, and the nature of solutions within different mathematical contexts. This article delves deep into the meaning and implications of x² + 17, examining its properties, applications, and the broader mathematical landscape it illuminates.
Introduction: A Deeper Look Beyond the Surface
At its core, x² + 17 represents a quadratic expression, a polynomial of degree two. This means the highest power of the variable x is 2. While seemingly basic, understanding quadratic expressions is fundamental to various fields like physics (modeling projectile motion), engineering (designing structures), and finance (analyzing investment growth). The constant term, 17, significantly influences the expression's behavior and the nature of its solutions. This article aims to unpack these influences, moving beyond a simple definition and exploring the rich mathematical tapestry woven around this seemingly simple expression.
Exploring the Solutions: Finding the Roots of x² + 17 = 0
One of the most common operations performed on a quadratic expression is setting it equal to zero and solving for x. This process of finding the roots (or zeros) of the equation x² + 17 = 0 reveals crucial information about the expression's behavior. Let's solve it:
x² + 17 = 0 x² = -17 x = ±√(-17)
Notice something intriguing? The solution involves the square root of a negative number. This introduces us to the realm of complex numbers. The solutions are complex conjugates:
x = √17i and x = -√17i
where i represents the imaginary unit, defined as √(-1). The presence of complex solutions highlights a key characteristic of x² + 17: it has no real roots. This means the parabola represented by the graph of y = x² + 17 never intersects the x-axis. This seemingly simple fact has profound implications when considering real-world applications where only real solutions are physically meaningful.
Graphical Representation: Visualizing the Expression
Visualizing the expression y = x² + 17 through a graph provides valuable insights. The graph is a parabola that opens upwards (because the coefficient of x² is positive). The vertex of the parabola is located at (0, 17), meaning the minimum value of the expression is 17. Since the parabola opens upwards and its vertex lies above the x-axis, it never crosses the x-axis, reinforcing our earlier conclusion that there are no real roots. This visual representation offers a powerful way to understand the behavior of the expression and its lack of real solutions.
The Role of the Constant Term: 17's Influence
The constant term, 17, plays a crucial role in shaping the expression's characteristics. It determines the vertical shift of the parabola. If we were to consider other quadratic expressions of the form x² + c, where c is a constant, changing c would shift the parabola vertically. If c is positive, the parabola lies entirely above the x-axis (like x² + 17), resulting in complex roots. If c is negative, the parabola intersects the x-axis at two points, yielding two real roots. If c is zero, the parabola touches the x-axis at only one point (the origin), resulting in a single real root. The value of 17 specifically positions the parabola high enough to avoid any intersection with the x-axis within the realm of real numbers.
Extending the Exploration: Variations and Generalizations
The expression x² + 17 can be extended and generalized in several ways. We can explore variations such as:
- x² + a, where a is any constant. This explores the impact of different constant terms on the roots and the graph.
- ax² + 17, where a is a constant. This introduces a coefficient for the x² term, influencing the parabola's width and direction of opening.
- ax² + bx + 17, where a and b are constants. This is the general form of a quadratic equation, encompassing a wider range of behaviors and solution types.
Exploring these variations provides a deeper understanding of the principles governing quadratic equations and their solutions. Each variation offers unique insights into the relationship between coefficients, roots, and the graphical representation.
Applications in Different Fields: Real-World Relevance
Although the equation x² + 17 = 0 doesn't have real solutions, the underlying concepts and techniques used to analyze it have widespread applications:
- Physics: Quadratic equations frequently arise in projectile motion problems, where the height of a projectile as a function of time is described by a quadratic equation. While the specific equation x² + 17 might not directly model a physical phenomenon, the mathematical tools used to analyze it are essential for solving related real-world problems.
- Engineering: Quadratic equations are crucial in structural design, analyzing stress and strain on materials. The ability to solve quadratic equations and understand the nature of their roots is essential for ensuring the stability and safety of structures.
- Finance: Quadratic equations can be used to model investment growth or decay. The concepts of roots and the behavior of quadratic functions are vital for analyzing investment strategies and predicting future returns.
These examples highlight that the seemingly simple expression x² + 17, while lacking real solutions in its basic form, represents a fundamental building block in solving more complex problems across various disciplines. The analytical techniques and underlying principles are highly relevant and applicable to real-world scenarios.
Connecting to Complex Numbers: A Broader Mathematical Perspective
The appearance of complex numbers in the solutions to x² + 17 = 0 offers a glimpse into a much broader and fascinating area of mathematics. Complex numbers extend the real number system, introducing a new dimension to mathematical operations and representations. They are essential in many advanced mathematical areas including:
- Electrical Engineering: Complex numbers are used extensively in analyzing alternating current (AC) circuits, allowing engineers to efficiently model and manipulate complex waveforms.
- Quantum Mechanics: Complex numbers play a central role in quantum mechanics, where wave functions describing the behavior of subatomic particles are complex-valued.
- Signal Processing: Complex numbers are indispensable tools in the field of signal processing, used for tasks such as filtering, modulation, and demodulation of signals.
Frequently Asked Questions (FAQ)
Q1: What does it mean that x² + 17 = 0 has no real solutions?
A1: It means there are no real numbers that, when squared and added to 17, result in zero. The solutions involve the imaginary unit i, leading to complex numbers. Graphically, this means the parabola representing y = x² + 17 never intersects the x-axis.
Q2: Why are complex numbers important?
A2: Complex numbers are crucial for solving certain types of equations that don't have real solutions. They also have extensive applications in various fields of science and engineering, as discussed earlier.
Q3: Can x² + 17 ever equal zero?
A3: Yes, but only if we expand our consideration to the realm of complex numbers. The solutions are x = √17i and x = -√17i.
Q4: How does the constant term affect the graph of a quadratic equation?
A4: The constant term determines the vertical shift of the parabola. A positive constant shifts the parabola upward, a negative constant shifts it downward, and a zero constant means the vertex lies on the x-axis.
Conclusion: A Simple Expression, Profound Implications
The seemingly simple expression x² + 17 offers a gateway to a rich and diverse range of mathematical concepts. From the fundamental principles of quadratic equations and their solutions to the fascinating world of complex numbers and their applications across various scientific disciplines, this expression serves as a powerful reminder of the interconnectedness and depth within mathematics. Its seemingly straightforward nature belies a complexity that highlights the power and beauty of mathematical exploration. By understanding this simple expression, we gain a deeper appreciation for the elegance and utility of mathematics in unraveling the mysteries of the universe.
Latest Posts
Latest Posts
-
34kg To Stone
Sep 14, 2025
-
Shah Mosque Isfahan
Sep 14, 2025
-
75 Of 12
Sep 14, 2025
-
103f To C
Sep 14, 2025
-
25ml To Oz
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 2 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.