75 Of 12
stanleys
Sep 14, 2025 · 5 min read
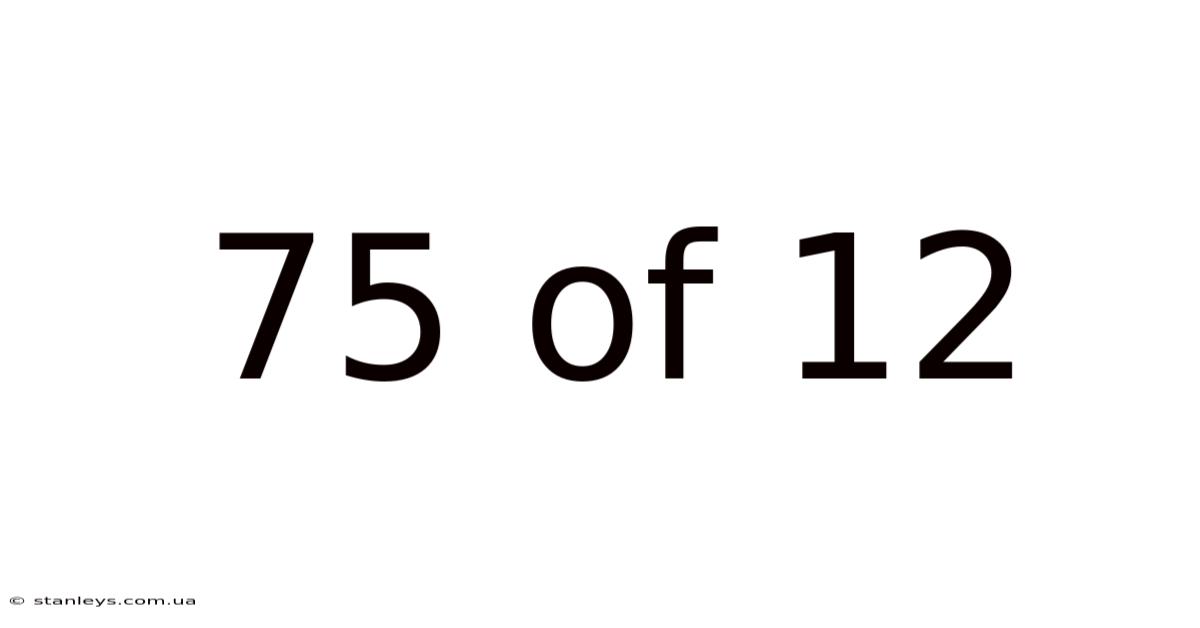
Table of Contents
Decoding the Fraction: Understanding 75/12 and its Implications
The seemingly simple fraction 75/12 might appear straightforward at first glance, but it holds a wealth of mathematical concepts within its seemingly small form. This article will delve deep into understanding 75/12, exploring its simplification, decimal representation, applications in real-world scenarios, and its connection to broader mathematical principles. We will also cover frequently asked questions to solidify your understanding of this fraction and its implications.
Introduction: Beyond the Surface of 75/12
Fractions, the building blocks of arithmetic and algebra, represent parts of a whole. 75/12, representing 75 parts out of a total of 12 parts, presents a unique opportunity to explore various mathematical operations and their practical applications. This seemingly simple fraction is a gateway to understanding concepts like simplification, improper fractions, mixed numbers, and decimal conversions. Mastering the manipulation of this specific fraction can significantly improve your understanding of broader mathematical principles.
Simplifying 75/12: Finding the Greatest Common Divisor (GCD)
Before exploring other representations, it's crucial to simplify the fraction 75/12 to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (75) and the denominator (12). The GCD is the largest number that divides both numbers without leaving a remainder.
Let's find the GCD of 75 and 12 using the prime factorization method:
- Prime factorization of 75: 3 x 5 x 5 = 3 x 5²
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
The common prime factor is 3. Therefore, the GCD of 75 and 12 is 3.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
75 ÷ 3 = 25 12 ÷ 3 = 4
Therefore, the simplified form of 75/12 is 25/4. This simplified fraction is easier to work with and represents the same value as the original fraction.
Converting 75/12 to a Mixed Number
An improper fraction, like 25/4 (or the original 75/12), has a numerator larger than its denominator. We can convert this improper fraction into a mixed number, which combines a whole number and a proper fraction.
To do this, we divide the numerator (25) by the denominator (4):
25 ÷ 4 = 6 with a remainder of 1.
This means that 25/4 represents 6 whole units and 1/4 of another unit. Therefore, the mixed number representation of 25/4 (and thus 75/12) is 6 1/4.
Decimal Representation of 75/12
Converting a fraction to a decimal involves dividing the numerator by the denominator. Using the simplified fraction 25/4:
25 ÷ 4 = 6.25
Therefore, the decimal representation of 75/12 is 6.25. This decimal form is useful for calculations and comparisons, especially when working with other decimal numbers.
Real-World Applications of 75/12
The fraction 75/12, and its simplified form 25/4 or mixed number 6 1/4, has various practical applications:
- Measurement: Imagine you have a length of 75 centimeters and need to divide it into 12 equal parts. Each part would measure 25/4 centimeters or 6.25 centimeters.
- Sharing: If you have 75 cookies to share equally among 12 friends, each friend would receive 25/4 cookies, or 6 and a quarter cookies.
- Baking: A recipe might call for 75 grams of flour, but you only want to make 12 servings. You would need to use 25/4 grams (6.25 grams) of flour for each serving.
- Financial Calculations: Imagine you have $75 and you want to split it evenly among 12 people. Each person would receive $6.25.
Further Mathematical Explorations: Ratios and Proportions
The fraction 75/12 can be viewed as a ratio, expressing the relationship between two quantities. Understanding this ratio allows you to solve problems involving proportions. For instance, if 75 represents the number of boys in a school and 12 represents the number of girls, the ratio of boys to girls is 75:12, which simplifies to 25:4. This means there are 25 boys for every 4 girls. This concept is crucial in various fields, including chemistry, physics, and engineering.
Understanding Percentage Representation
To express 75/12 as a percentage, we first convert it to a decimal (6.25) and then multiply by 100:
6.25 x 100 = 625%
This indicates that 75 is 625% of 12. This percentage representation offers another way to understand the relationship between the numerator and the denominator.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify 75/12 any further than 25/4?
A: No. 25 and 4 have no common factors other than 1, meaning 25/4 is in its simplest form.
-
Q: What is the difference between an improper fraction and a mixed number?
A: An improper fraction has a numerator greater than or equal to the denominator (e.g., 75/12 or 25/4). A mixed number combines a whole number and a proper fraction (e.g., 6 1/4).
-
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to work with in calculations and comparisons. It also provides a clearer understanding of the relationship between the numerator and the denominator.
-
Q: Are there other methods to find the GCD besides prime factorization?
A: Yes, the Euclidean algorithm is another efficient method for finding the greatest common divisor of two numbers.
-
Q: How can I convert a decimal back to a fraction?
A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (e.g., 6.25 = 625/100). Then, simplify the fraction to its lowest terms.
Conclusion: Mastering Fractions – One Step at a Time
Understanding the fraction 75/12 goes beyond simply knowing its simplified form. It involves grasping the underlying principles of simplification, conversion between different representations (mixed numbers and decimals), and the application of these concepts in various real-world situations. By exploring this single fraction, we've touched upon fundamental mathematical concepts that are crucial for success in higher-level mathematics and problem-solving in various disciplines. The journey from 75/12 to its simplified form, its decimal equivalent, and its applications highlights the power and versatility of fractions as a fundamental tool in mathematics. Remember, the key is consistent practice and a willingness to explore the underlying mathematical principles.
Latest Posts
Latest Posts
-
List Of Jurors
Sep 14, 2025
-
1 Of 1500
Sep 14, 2025
-
Arrays For Math
Sep 14, 2025
-
70 Of 10
Sep 14, 2025
-
48 7kg In Stone
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.