Simplify 8 10
stanleys
Sep 12, 2025 · 6 min read
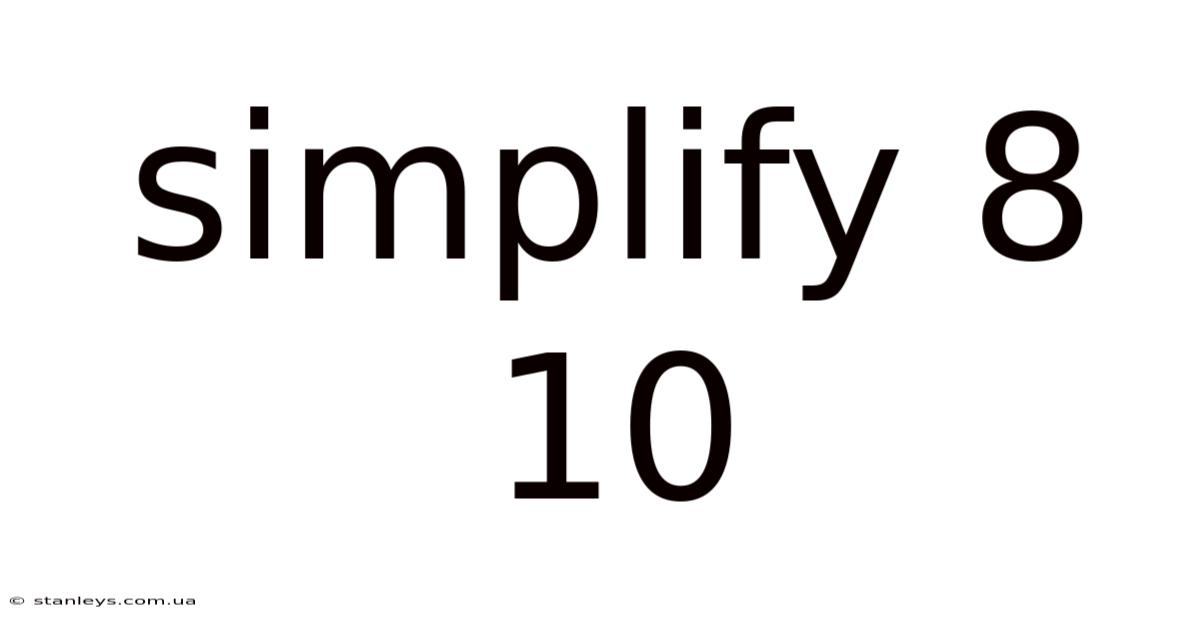
Table of Contents
Simplifying 8/10: A Comprehensive Guide to Fraction Reduction
Understanding fractions is a fundamental skill in mathematics, crucial for everything from basic arithmetic to advanced calculus. This article will delve into the seemingly simple task of simplifying the fraction 8/10, exploring not only the mechanics of reduction but also the underlying mathematical principles and applications. We'll cover various methods, explain the importance of simplification, and answer frequently asked questions to solidify your understanding of this essential concept. Learn how to simplify fractions and master this core mathematical skill.
Understanding Fractions: A Quick Refresher
Before we tackle 8/10, let's briefly review the basics of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a horizontal line (the fraction bar). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 8/10, 8 is the numerator and 10 is the denominator. This means we have 8 parts out of a total of 10 equal parts.
Simplifying Fractions: The Concept of Greatest Common Divisor (GCD)
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This is achieved by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Method 1: Finding the GCD through Prime Factorization
This method involves breaking down the numerator and denominator into their prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Steps:
-
Find the prime factorization of the numerator (8): 8 = 2 x 2 x 2 = 2³
-
Find the prime factorization of the denominator (10): 10 = 2 x 5
-
Identify common prime factors: Both 8 and 10 share one common prime factor: 2.
-
Calculate the GCD: The GCD is the product of the common prime factors raised to the lowest power. In this case, the GCD is 2¹.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD (2):
8 ÷ 2 = 4 10 ÷ 2 = 5
Therefore, the simplified form of 8/10 is 4/5.
Method 2: Finding the GCD through Listing Factors
This method is suitable for smaller numbers and involves listing all the factors (numbers that divide evenly) of both the numerator and denominator.
Steps:
-
List the factors of 8: 1, 2, 4, 8
-
List the factors of 10: 1, 2, 5, 10
-
Identify the common factors: The common factors of 8 and 10 are 1 and 2.
-
Determine the GCD: The greatest common factor is 2.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD (2):
8 ÷ 2 = 4 10 ÷ 2 = 5
Again, the simplified fraction is 4/5.
Method 3: Using the Euclidean Algorithm
The Euclidean algorithm is a more efficient method for finding the GCD of larger numbers. It's based on the principle that the GCD of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, which is the GCD.
Steps:
-
Start with the numerator (8) and denominator (10):
-
Subtract the smaller number from the larger number: 10 - 8 = 2
-
Replace the larger number with the result: Now we have 8 and 2.
-
Repeat the subtraction: 8 - 2 = 6; then 6 - 2 = 4; then 4 - 2 = 2.
-
Continue until the numbers are equal: We are left with 2 and 2. The GCD is 2.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD (2):
8 ÷ 2 = 4 10 ÷ 2 = 5
Once again, the simplified fraction is 4/5.
Why Simplify Fractions?
Simplifying fractions is crucial for several reasons:
-
Clarity: Simplified fractions are easier to understand and interpret. 4/5 is more readily grasped than 8/10.
-
Efficiency: Simplified fractions make calculations simpler and faster. Working with 4/5 is generally easier than working with 8/10, especially in more complex calculations.
-
Standardization: Simplifying fractions ensures consistency and facilitates comparison between different fractions.
-
Accuracy: In many contexts, particularly in science and engineering, simplified fractions are essential for accurate representation and calculations.
Applications of Fraction Simplification
Fraction simplification is not just a theoretical exercise; it has wide-ranging practical applications in various fields:
-
Cooking and Baking: Following recipes often requires understanding and simplifying fractions to measure ingredients accurately.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on fraction simplification for accurate results.
-
Finance and Accounting: Working with percentages and proportions in financial calculations necessitates a strong understanding of fraction simplification.
-
Data Analysis: Simplifying fractions can improve clarity and interpretation of data in statistical analysis.
Frequently Asked Questions (FAQ)
Q: What if the numerator and denominator have no common factors other than 1?
A: If the numerator and denominator share no common factors other than 1, the fraction is already in its simplest form. It cannot be simplified further.
Q: Can I simplify a fraction by dividing the numerator and denominator by any number?
A: You can divide the numerator and denominator by any common factor, but to get the simplest form, you must divide by the greatest common factor (GCD).
Q: What happens if I divide by a factor that is not the GCD?
A: If you divide by a common factor that isn't the GCD, you'll get a simplified fraction, but it won't be in its lowest terms. You would then need to simplify further.
Q: Are there any shortcuts for simplifying fractions?
A: For smaller numbers, you can often spot common factors easily. However, for larger numbers, the methods described above – prime factorization, listing factors, or the Euclidean algorithm – are more reliable and efficient.
Q: What if the fraction is an improper fraction (numerator is larger than the denominator)?
A: Even improper fractions can be simplified. Simplify the fraction as usual by finding the GCD and dividing both the numerator and the denominator. You can then convert the simplified fraction to a mixed number if needed.
Conclusion
Simplifying the fraction 8/10 to its simplest form, 4/5, is a straightforward process once you grasp the fundamental concepts of greatest common divisors and prime factorization. Mastering this skill is not just about getting the right answer; it’s about understanding the underlying principles and appreciating the wider applications of fraction simplification in various fields. Through consistent practice and a thorough understanding of the different methods, you can confidently tackle fraction simplification and build a strong foundation in mathematics. Remember, the key is to find the greatest common divisor and divide both the numerator and denominator by it to arrive at the simplest form.
Latest Posts
Latest Posts
-
1800 X 12
Sep 12, 2025
-
Algebraic Notation Algebra
Sep 12, 2025
-
180 2
Sep 12, 2025
-
Functionalism And Education
Sep 12, 2025
-
61 6kg In Stone
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Simplify 8 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.