180 / 2
stanleys
Sep 12, 2025 · 6 min read
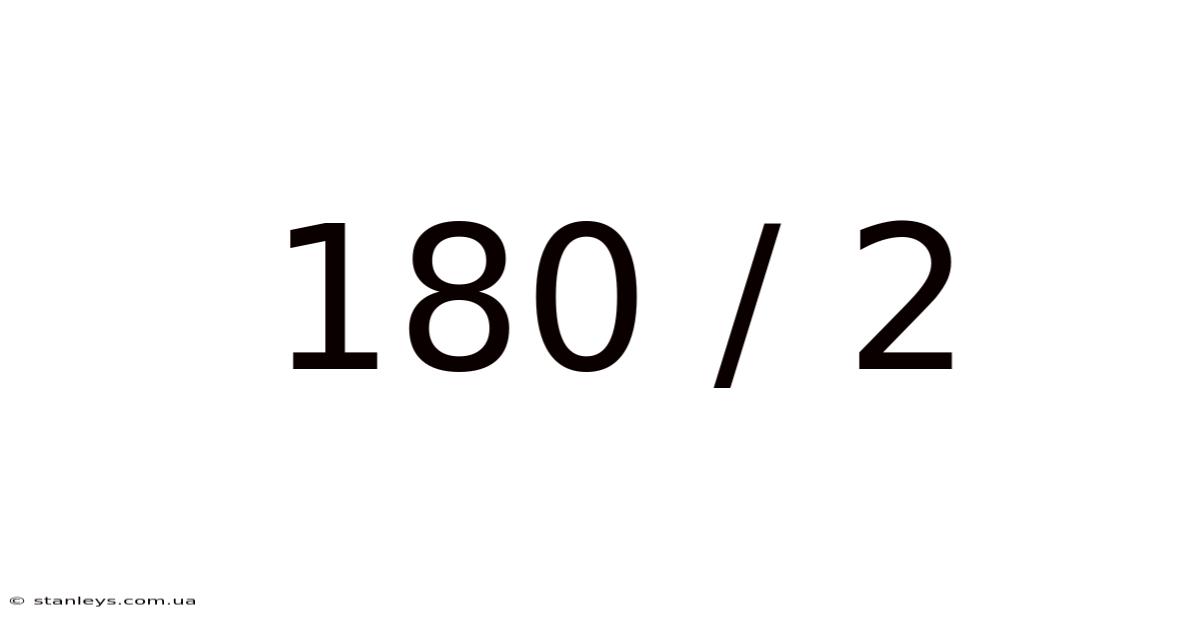
Table of Contents
Decoding 180 / 2: A Deep Dive into Division and its Applications
This article explores the seemingly simple mathematical operation of 180 / 2, delving far beyond the immediate answer. We'll uncover the underlying principles of division, explore its various applications across different fields, and touch upon the historical significance of this fundamental arithmetic operation. Understanding 180 / 2 provides a gateway to comprehending more complex mathematical concepts and their real-world relevance.
Introduction: The Basics of Division
Division, at its core, is the inverse operation of multiplication. While multiplication involves combining equal groups, division separates a quantity into equal parts. The expression 180 / 2 asks: "How many times does 2 go into 180?" The answer, 90, represents the number of times 2 fits evenly into 180. This simple equation forms the foundation for countless applications in various aspects of life. Understanding division is crucial for problem-solving in mathematics, science, engineering, finance, and everyday life.
Calculating 180 / 2: Step-by-Step
While the answer to 180 / 2 is readily apparent to many, let's break down the calculation methodically to reinforce fundamental principles. Several methods exist, each with its own merits:
1. Long Division: This traditional method provides a systematic approach, particularly useful for more complex division problems.
- Step 1: Set up the problem: 2 | 180
- Step 2: Divide the first digit (1) by the divisor (2). Since 1 is smaller than 2, we move to the next digit.
- Step 3: Divide 18 by 2. This equals 9. Write 9 above the 8.
- Step 4: Multiply the quotient (9) by the divisor (2): 9 x 2 = 18. Write 18 below 18.
- Step 5: Subtract 18 from 18: 18 - 18 = 0.
- Step 6: Bring down the next digit (0).
- Step 7: Divide 0 by 2: 0. Write 0 above the 0.
- Step 8: The final quotient is 90.
2. Repeated Subtraction: This method visually demonstrates the concept of division as repeated subtraction. We repeatedly subtract the divisor (2) from the dividend (180) until we reach zero. The number of times we subtract represents the quotient. While effective for smaller numbers, this becomes less practical for larger divisions.
3. Using Multiplication Facts: Recognizing that 2 x 90 = 180 directly provides the answer. This method relies on memorized multiplication tables and is highly efficient for familiar numbers.
Regardless of the method employed, the result remains consistent: 180 / 2 = 90.
Real-World Applications of Division: Beyond the Classroom
Division isn't confined to textbooks; its applications are pervasive in our daily lives and various professions.
1. Everyday Life:
- Sharing: Dividing a pizza among friends, splitting a bill at a restaurant, or equally distributing candies among children all involve the fundamental concept of division.
- Cooking & Baking: Scaling recipes up or down, calculating ingredient quantities based on the number of servings, and determining portion sizes all rely on division.
- Travel: Calculating fuel consumption, determining travel time based on distance and speed, and dividing a journey into segments are examples of everyday division.
2. Business & Finance:
- Profit Sharing: Dividing profits among business partners or shareholders is a crucial aspect of financial management.
- Budgeting: Allocating resources, distributing funds across various departments, and calculating per-unit costs all involve division.
- Pricing: Determining the cost per item, calculating discounts, and establishing profit margins often require division.
3. Science & Engineering:
- Physics: Calculating average speeds, determining densities, and solving numerous physics equations rely on division.
- Chemistry: Calculating molar masses, determining concentrations of solutions, and balancing chemical equations all utilize division.
- Engineering: Dividing workloads among teams, calculating material requirements based on project specifications, and determining structural load-bearing capacities often involve division.
4. Computer Science:
- Data Processing: Dividing large datasets into smaller, manageable chunks for processing is fundamental to efficient data management.
- Algorithm Design: Many algorithms employ division as a core operation for tasks such as sorting, searching, and optimization.
- Networking: Dividing network bandwidth among users and managing data packets across a network requires division.
The Historical Significance of Division
Division's history is interwoven with the development of mathematics itself. Early civilizations employed various techniques for dividing quantities, reflecting the importance of fair distribution and resource management. Evidence suggests that ancient Egyptians, Babylonians, and Greeks used sophisticated methods for division, albeit without the symbolic notation we use today. The development of algorithms and computational methods significantly advanced the ease and efficiency of performing division, paving the way for the modern mathematical framework we utilize.
Division and its Relationship to Other Mathematical Operations
Division is inextricably linked to other arithmetic operations. It's the inverse of multiplication, meaning that division "undoes" multiplication. It's also closely related to addition and subtraction, as repeated subtraction can be used to solve division problems. Furthermore, understanding division is essential for mastering more advanced mathematical concepts like fractions, decimals, percentages, and algebra.
Understanding Remainders in Division
While 180 / 2 results in an even division with no remainder, many division problems yield a remainder. A remainder is the amount left over after dividing as evenly as possible. For instance, 181 / 2 = 90 with a remainder of 1. Understanding remainders is crucial in various applications, such as determining whether a number is even or odd, and in programming and computer science for handling incomplete divisions.
Advanced Concepts Related to Division: Fractions and Decimals
The result of a division can be expressed as a whole number (like 90 in our example), a fraction, or a decimal. When dividing numbers that don't result in a whole number, the result can be represented as a fraction (e.g., 181/2 can be expressed as the mixed fraction 90 1/2) or a decimal (90.5). Understanding fractions and decimals is essential for extending our understanding of division beyond whole numbers.
Frequently Asked Questions (FAQs)
Q: What if I need to divide a number by zero?
A: Dividing by zero is undefined in mathematics. It's a fundamental rule because there's no number that, when multiplied by zero, will result in a non-zero number.
Q: How do I divide larger numbers?
A: For larger numbers, long division or a calculator is recommended. Long division provides a systematic approach, while calculators offer a quick and convenient method.
Q: Are there different types of division?
A: While the basic principle remains the same, different types of division exist depending on the context, such as integer division (yielding a whole number quotient and a remainder) and floating-point division (yielding a decimal result).
Q: How is division used in programming?
A: Division is a fundamental operation in programming used in various algorithms and calculations. The specific implementation might vary depending on the programming language and data types used.
Conclusion: The Enduring Importance of Division
The seemingly simple calculation of 180 / 2 reveals a depth of mathematical principles and real-world applications far exceeding its initial appearance. From everyday tasks to complex scientific and engineering problems, division plays a critical role in our understanding of the world. Mastering this fundamental operation unlocks a deeper understanding of mathematics and its power to solve problems across diverse fields. This exploration of 180 / 2 serves not just as an answer but as a gateway to appreciating the profound implications of a seemingly simple mathematical concept. It emphasizes the importance of understanding the underlying principles of mathematical operations and their widespread applicability in various aspects of life.
Latest Posts
Latest Posts
-
Grains In Gramm
Sep 12, 2025
-
91km In Miles
Sep 12, 2025
-
93 3kg In Stone
Sep 12, 2025
-
93 9kg In Stone
Sep 12, 2025
-
Lb En Newton
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 180 / 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.