Rpm In Rad/s
stanleys
Sep 11, 2025 · 5 min read
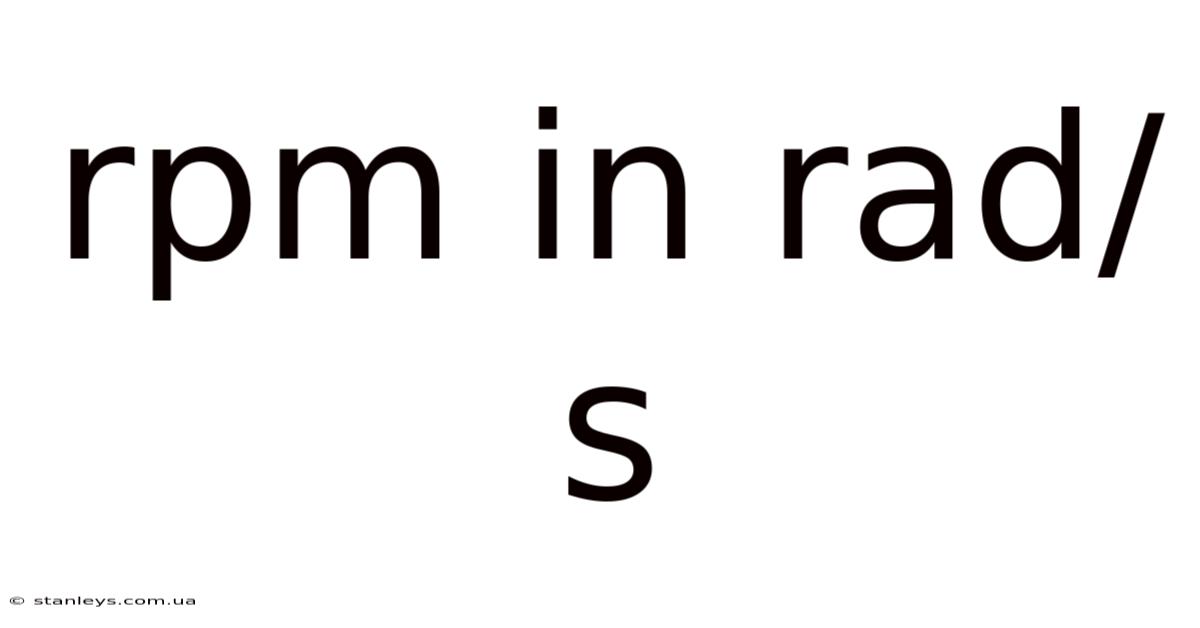
Table of Contents
Understanding RPM and its Conversion to Rad/s: A Comprehensive Guide
Revolutions per minute (RPM) is a common unit for measuring rotational speed, frequently encountered in various fields like engineering, mechanics, and even everyday appliances. However, in many scientific and engineering calculations, it's more convenient to use radians per second (rad/s), which is an SI unit representing angular velocity. This article provides a comprehensive understanding of RPM, explains the conversion process to rad/s, explores its applications, and answers frequently asked questions. We'll delve into the underlying mathematics and provide practical examples to solidify your understanding.
Understanding RPM (Revolutions Per Minute)
RPM, or revolutions per minute, is a unit of rotational speed that describes how many complete rotations an object makes around a fixed axis in one minute. Imagine a spinning wheel; its RPM tells us how many times it completes a full circle in 60 seconds. It's a widely used and easily understood measure of rotational frequency, particularly in contexts involving motors, engines, and rotating machinery.
- Practical Applications of RPM: RPM is crucial in various applications, including:
- Engine speed: Car engines, generators, and turbines operate at specific RPMs.
- Motor control: Industrial motors and electric motors often have their speed regulated in RPM.
- Disc drives: Hard drives and CD/DVD players operate at specific RPMs to read data.
- Manufacturing processes: Many manufacturing processes rely on machines operating at precise RPMs for consistent output.
Understanding Rad/s (Radians Per Second)
Radians per second (rad/s) is the SI unit of angular velocity. Angular velocity describes how quickly the angle of an object changes with respect to time. A radian is a unit of angular measurement defined as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle. One full revolution around a circle corresponds to 2π radians. Therefore, rad/s expresses the rate of change of angular position in terms of radians per second.
- Why Use Rad/s? While RPM is intuitive, rad/s offers several advantages in scientific and engineering applications:
- Consistency with SI units: It aligns with the International System of Units, facilitating easier calculations and compatibility across various disciplines.
- Mathematical simplicity: It simplifies many mathematical equations and formulas related to rotational motion and dynamics, particularly those involving calculus and differential equations.
- Unified framework: It provides a unified approach to describing both linear and angular motion, allowing for easier comparison and analysis of different types of motion.
Converting RPM to Rad/s: The Conversion Formula
The conversion between RPM and rad/s is straightforward. We need to consider that one revolution is equal to 2π radians and one minute is equal to 60 seconds. Therefore, the conversion formula is:
ω (rad/s) = (2π * N (RPM)) / 60
Where:
- ω represents angular velocity in rad/s.
- N represents rotational speed in RPM.
This formula effectively converts the rotational speed from revolutions per minute to radians per second by incorporating the conversion factors for radians and seconds.
Let's illustrate this with an example:
A motor spins at 1500 RPM. What is its angular velocity in rad/s?
ω (rad/s) = (2π * 1500 RPM) / 60 = 50π rad/s ≈ 157.08 rad/s
Converting Rad/s to RPM: The Reverse Conversion
The reverse conversion from rad/s to RPM is equally simple. We just rearrange the formula above:
N (RPM) = (ω (rad/s) * 60) / (2π)
Let's illustrate this with an example:
A rotating shaft has an angular velocity of 100 rad/s. What is its speed in RPM?
N (RPM) = (100 rad/s * 60) / (2π) ≈ 954.93 RPM
Applications of RPM to Rad/s Conversion
The conversion between RPM and rad/s is vital in various engineering and scientific contexts. Here are a few key applications:
-
Calculating Torque and Power: In mechanical engineering, the conversion is essential for calculating torque and power transmitted by rotating shafts and machinery. Many formulas for power and torque use angular velocity in rad/s.
-
Control Systems: In control systems design, the rotational speed of motors and actuators is often specified in rad/s for precise control algorithms. Converting from RPM is necessary for effective integration.
-
Robotics: Robotics involves significant rotational motion. Understanding and converting between RPM and rad/s is crucial for controlling the speed and precision of robotic manipulators and actuators.
-
Aerodynamics and Fluid Mechanics: In aerodynamics and fluid mechanics, rotational speed often impacts the behavior of fluids and gases. Converting RPM to rad/s is crucial for using relevant equations and analysis.
Advanced Concepts: Angular Acceleration
Beyond simple conversion, understanding angular acceleration is crucial in dynamics. Angular acceleration (α) is the rate of change of angular velocity, expressed in rad/s². If the RPM (and therefore angular velocity) is changing, we need to consider this acceleration. The conversion from RPM to rad/s is still a crucial first step before calculating angular acceleration.
Frequently Asked Questions (FAQ)
Q1: Why is rad/s preferred over RPM in many scientific calculations?
A1: Rad/s is the SI unit of angular velocity, making it consistent with other SI units used in calculations. Its use simplifies many formulas, especially those involving calculus and differential equations describing rotational motion.
Q2: Can I use this conversion for any rotating object, regardless of size?
A2: Yes, the conversion formula is universally applicable to any object undergoing rotational motion, irrespective of its size or shape.
Q3: What if the RPM is not constant?
A3: If the RPM is not constant (meaning the angular velocity is changing), you'll need to work with instantaneous angular velocity and angular acceleration. The conversion at any specific moment still uses the same formula, but you'll need to account for the changing RPM over time.
Q4: Are there any other units for rotational speed besides RPM and rad/s?
A4: Yes, other units exist, such as revolutions per second (rps), degrees per second, and even cycles per second (Hertz), depending on the context. However, RPM and rad/s are the most common in engineering and science.
Conclusion
Understanding the relationship between RPM and rad/s is fundamental for anyone working with rotational motion. The conversion between these two units is relatively straightforward yet crucial for accurate calculations and a unified approach to describing rotational dynamics. This article has provided a comprehensive overview of the concept, including practical examples and frequently asked questions, equipping you with the knowledge to confidently handle conversions and apply them in various contexts. Remember the core conversion formula and its implications—it's a key stepping stone to mastering more advanced concepts in mechanics and engineering.
Latest Posts
Latest Posts
-
94 6kg In Stone
Sep 11, 2025
-
1 5 X 4
Sep 11, 2025
-
20 Of 25 00
Sep 11, 2025
-
Mi To Yd
Sep 11, 2025
-
The Dancing Trees
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Rpm In Rad/s . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.