20 Of 25.00
stanleys
Sep 11, 2025 · 5 min read
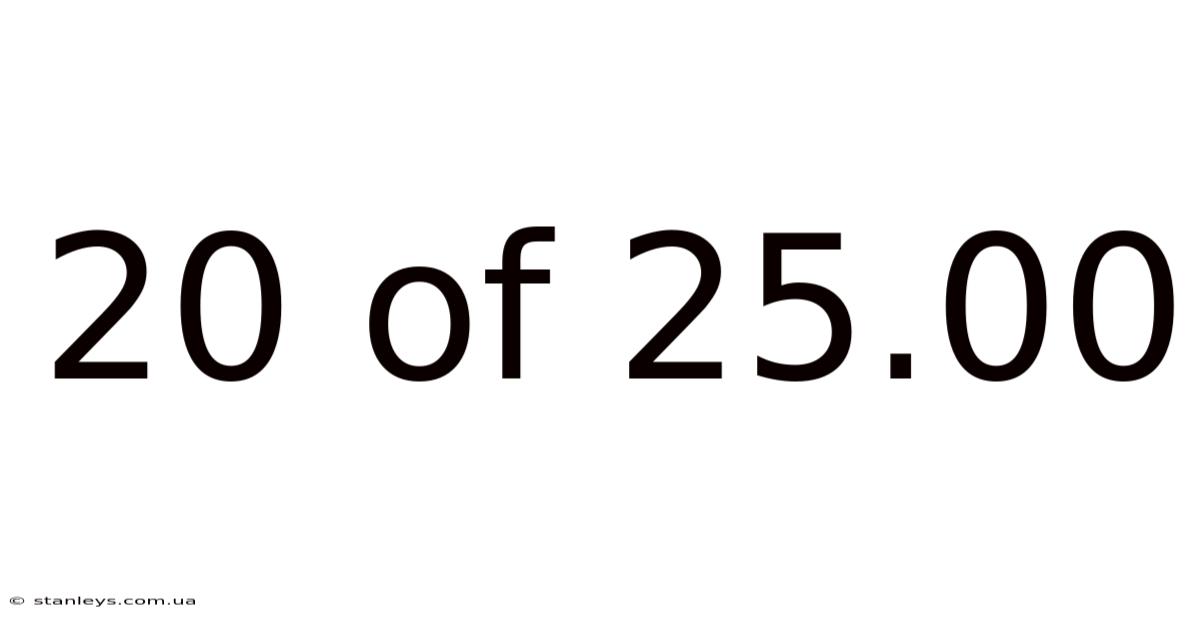
Table of Contents
Decoding 20 of 25.00: Understanding Proportions, Percentages, and Their Applications
Understanding fractions, decimals, and percentages is fundamental to navigating the world around us. Whether you're calculating discounts, understanding financial reports, or mastering scientific concepts, the ability to interpret and manipulate these numerical representations is crucial. This article delves into the meaning of "20 of 25.00," exploring its representation as a fraction, decimal, and percentage, and showcasing its applications in various real-world scenarios. We will also address common misconceptions and provide a comprehensive understanding of proportional relationships. This will equip you with the skills to confidently tackle similar numerical problems.
Understanding the Fundamentals: Fractions, Decimals, and Percentages
Before we delve into "20 of 25.00," let's establish a solid understanding of the core concepts.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one part out of two equal parts.
-
Decimals: Decimals are another way to represent fractions. They use a base-ten system, with the decimal point separating the whole number from the fractional part. For example, 0.5 is equivalent to 1/2.
-
Percentages: Percentages represent a fraction or decimal as a proportion of 100. The symbol "%" indicates "per hundred." For example, 50% is equivalent to 50/100, which simplifies to 1/2 or 0.5.
Analyzing "20 of 25.00": A Step-by-Step Approach
"20 of 25.00" can be interpreted as 20 out of 25. Let's explore its representation in different forms:
1. As a Fraction:
The simplest representation is the fraction 20/25. This fraction can be simplified by finding the greatest common divisor (GCD) of 20 and 25, which is 5. Dividing both the numerator and the denominator by 5, we get the simplified fraction 4/5.
2. As a Decimal:
To convert the fraction 4/5 to a decimal, we divide the numerator (4) by the denominator (5): 4 ÷ 5 = 0.8.
3. As a Percentage:
To convert the decimal 0.8 to a percentage, we multiply it by 100: 0.8 × 100 = 80%. Therefore, "20 of 25.00" represents 80%.
Real-World Applications: Putting it into Practice
The concept of "20 of 25.00," or its equivalent 80%, has numerous applications in various fields:
-
Academic Performance: If a student answers 20 out of 25 questions correctly on a test, their score is 80%.
-
Sales and Discounts: A store offering an 80% discount on an item means the customer pays only 20% of the original price.
-
Financial Analysis: In financial statements, percentages are used to represent proportions of revenue, expenses, and profits. For example, 80% of a company's revenue might come from a specific product line.
-
Statistical Analysis: Percentages are essential in statistical analysis for representing proportions within data sets. For example, 80% of survey respondents might agree with a particular statement.
-
Scientific Measurements: In scientific experiments, percentages are used to express the yield of a reaction or the concentration of a solution.
-
Probability: The probability of an event occurring can be expressed as a percentage. For instance, there's an 80% chance of rain.
Beyond the Basics: Exploring Proportional Relationships
Understanding "20 of 25.00" involves understanding proportional relationships. A proportion is a statement that two ratios are equal. In this case, the ratio 20/25 is proportional to the ratios 4/5, 0.8/1, and 80/100. These ratios all represent the same proportion – 80%.
Proportional reasoning is a crucial skill for solving various problems, including:
-
Scaling Recipes: If a recipe calls for 2 cups of flour and 1 cup of sugar, and you want to double the recipe, you'll need to maintain the proportion by doubling both ingredients.
-
Map Scales: Maps use scales to represent distances. Understanding proportions helps translate distances on a map to real-world distances.
-
Unit Conversions: Converting between different units, such as kilometers to miles or liters to gallons, relies on understanding proportions.
Addressing Common Misconceptions
Some common misconceptions surrounding fractions, decimals, and percentages include:
-
Confusing numerator and denominator: Remember, the numerator is the top number and the denominator is the bottom number in a fraction.
-
Incorrect decimal-to-percentage conversion: To convert a decimal to a percentage, multiply by 100, not divide.
-
Oversimplification of complex proportions: Always ensure you understand the context of the proportion before attempting to simplify it. A seemingly simple proportion might represent a complex relationship.
Frequently Asked Questions (FAQ)
Q: How do I convert a fraction to a decimal?
A: To convert a fraction to a decimal, divide the numerator by the denominator.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100 and add the percent symbol (%).
Q: How do I convert a percentage to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction.
Q: What is the significance of understanding proportions?
A: Understanding proportions is crucial for solving problems involving scaling, ratios, and percentages across various fields.
Q: Are there any online resources for practicing these concepts?
A: Numerous online resources, including educational websites and apps, offer practice exercises and interactive tutorials on fractions, decimals, and percentages.
Conclusion: Mastering Numerical Representations
Understanding "20 of 25.00" as 80% is not just about simple calculation; it's about grasping the fundamental concepts of fractions, decimals, and percentages. These concepts are intertwined and crucial for navigating various aspects of life, from academic pursuits to professional endeavors. By mastering these concepts and applying proportional reasoning, you enhance your problem-solving skills and develop a deeper understanding of the numerical world around you. Continue practicing and exploring different applications to solidify your understanding and build confidence in tackling similar numerical problems in the future. The more you practice, the more intuitive these concepts will become. Remember, understanding these foundational skills lays the groundwork for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
20 Of 5
Sep 11, 2025
-
X 3 9
Sep 11, 2025
-
Vernon Dalhart Songs
Sep 11, 2025
-
3 5 As Fraction
Sep 11, 2025
-
68 9kg In Stone
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 25.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.