Fully Factorise 12t+20
stanleys
Sep 12, 2025 · 5 min read
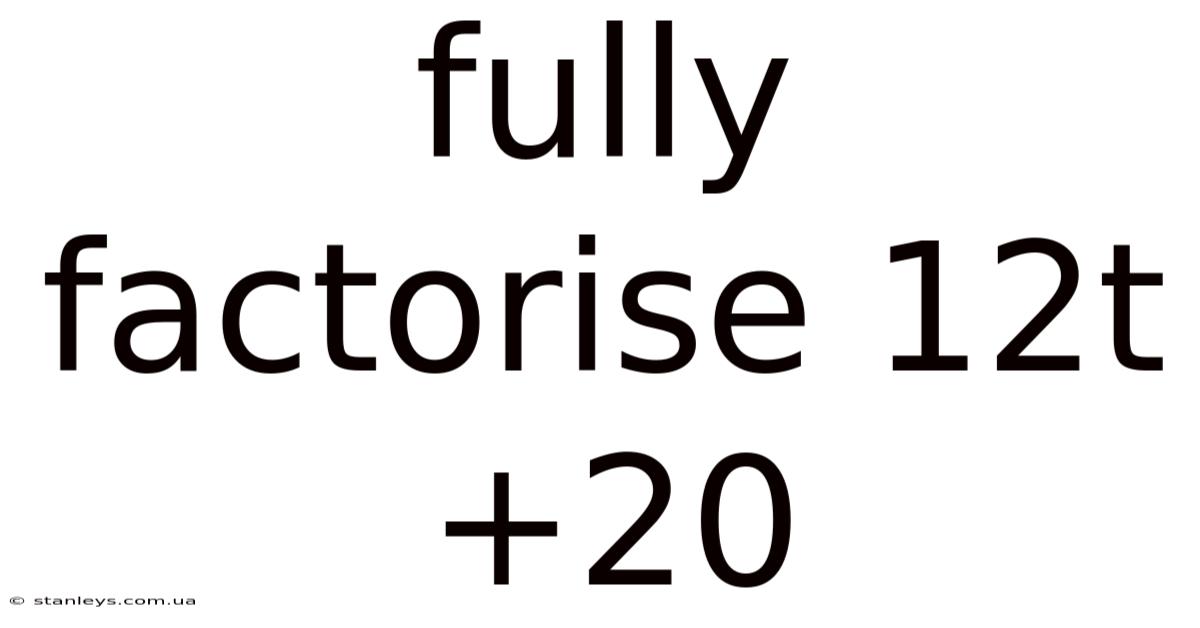
Table of Contents
Fully Factorising 12t + 20: A Comprehensive Guide
Fully factorising algebraic expressions is a fundamental skill in algebra. Understanding this process allows you to simplify complex expressions, solve equations, and ultimately, grasp more advanced mathematical concepts. This article provides a detailed explanation of how to fully factorise the expression 12t + 20, covering the underlying principles and offering a step-by-step approach suitable for beginners and a refresher for those needing a more thorough understanding. We'll explore different factoring techniques and delve into the reasons behind each step, ensuring a comprehensive grasp of the concept.
Understanding Factorisation
Before diving into the factorisation of 12t + 20, let's establish a clear understanding of what factorisation means. In essence, factorisation is the process of breaking down a mathematical expression into smaller, simpler expressions that, when multiplied together, produce the original expression. Think of it like reverse multiplication. For example, if you have the number 12, you can factorise it as 2 x 6, or 3 x 4, or 2 x 2 x 3. Similarly, algebraic expressions can be factorised into their constituent parts.
The goal of fully factorising an expression is to find the simplest possible factors, meaning that no further common factors exist among them. This is crucial for simplification and further manipulation of algebraic expressions.
Step-by-Step Factorisation of 12t + 20
The expression we're tasked with factorising is 12t + 20. The key to factorising this expression lies in identifying the greatest common factor (GCF) of the two terms, 12t and 20.
-
Identify the Coefficients and Variables: We have two terms: 12t and 20. The coefficient of the first term is 12, and it contains the variable 't'. The second term's coefficient is 20, and it doesn't contain any variables.
-
Find the Greatest Common Factor (GCF): To find the GCF, we need to find the largest number that divides both 12 and 20 evenly. Let's find the prime factors of each number:
- 12 = 2 x 2 x 3 (2² x 3)
- 20 = 2 x 2 x 5 (2² x 5)
The common factors are 2 x 2 = 4. Therefore, the GCF of 12 and 20 is 4.
-
Factor out the GCF: Now that we've identified the GCF as 4, we factor it out from both terms of the expression:
12t + 20 = 4(3t) + 4(5)
-
Rewrite the Expression: Notice that the GCF, 4, is now a common factor in both terms. We can rewrite the expression by factoring out the 4:
12t + 20 = 4(3t + 5)
This is the fully factorised form of the expression 12t + 20. No further common factors exist between 3t and 5.
Why This Method Works: The Distributive Property
The method we employed relies on the distributive property of multiplication, which states that a(b + c) = ab + ac. In our case, we essentially reversed this process. We started with ab + ac (12t + 20) and identified the common factor 'a' (4) to rewrite it in the form a(b + c) [4(3t + 5)].
Checking Your Answer
It's always a good practice to check your answer by expanding the factorised expression:
4(3t + 5) = 4 * 3t + 4 * 5 = 12t + 20
Since expanding the factorised expression gives us the original expression, we know our factorisation is correct.
Further Exploration: Factorising More Complex Expressions
While 12t + 20 is a relatively simple example, the same principles apply to more complex expressions. Let's look at some variations and explore how the approach changes:
-
Expressions with Multiple Variables: Consider the expression 6xy + 9x. The GCF here is 3x. Factoring it out gives: 3x(2y + 3).
-
Expressions with Negative Coefficients: Consider the expression -15a - 25. The GCF is 5, but since the leading term is negative, it's best practice to factor out -5: -5(3a + 5)
-
Expressions Requiring Grouping: For more complex expressions, you might need to use grouping techniques. For instance, to factorise 2x² + 4x + 3xy + 6y, you would group terms: (2x² + 4x) + (3xy + 6y) = 2x(x + 2) + 3y(x + 2). Now, (x+2) is a common factor, leading to (x+2)(2x+3y).
-
Recognising Special Forms: Learn to identify special forms like difference of squares (a² - b² = (a + b)(a - b)) and perfect squares (a² + 2ab + b² = (a + b)²). These shortcuts can significantly simplify the factorisation process.
Common Mistakes to Avoid
-
Not finding the greatest common factor: Always ensure you've identified the largest common factor. Failing to do so leaves the expression incompletely factorised.
-
Incorrectly applying the distributive property: Double-check your work by expanding the factorised expression to ensure it matches the original expression.
-
Forgetting to consider negative factors: When dealing with negative coefficients, remember that you can factor out a negative GCF to simplify the expression.
-
Overlooking special forms: Familiarize yourself with the common special forms to speed up your factorisation process.
Frequently Asked Questions (FAQ)
Q1: What happens if there's no common factor?
A1: If there's no common factor between the terms of an expression, it means the expression is already in its simplest form and cannot be further factorised.
Q2: Is there only one way to factorise an expression?
A2: While there might be different ways to factorise an expression, the fully factorised form should always be the same. For instance, 12t + 20 could be initially factorised as 2(6t + 10), but this is not fully factorised because 2 is still a common factor within the bracket. The fully factorised form remains 4(3t+5).
Q3: How can I improve my factorisation skills?
A3: Practice is key! Work through a variety of examples, starting with simpler expressions and gradually progressing to more complex ones. Pay attention to the principles and techniques discussed in this article.
Conclusion
Fully factorising algebraic expressions, like 12t + 20, is a fundamental building block in algebra. Understanding the concept of the greatest common factor (GCF) and applying the distributive property are crucial steps in mastering this skill. By following the step-by-step approach outlined in this article, and by practicing regularly, you can confidently factorise even more complex algebraic expressions. Remember to check your work and explore different techniques to enhance your understanding and problem-solving abilities. The ability to fully factorise expressions is a testament to your growing proficiency in algebra and paves the way for tackling more intricate mathematical challenges. Keep practicing, and you'll soon find this process becomes second nature!
Latest Posts
Latest Posts
-
81kg In Lb
Sep 12, 2025
-
42kg In Lbs
Sep 12, 2025
-
1 3 Of 36
Sep 12, 2025
-
Dl I Liter
Sep 12, 2025
-
115lbs To Kg
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Fully Factorise 12t+20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.