1/3 Of 36
stanleys
Sep 12, 2025 · 5 min read
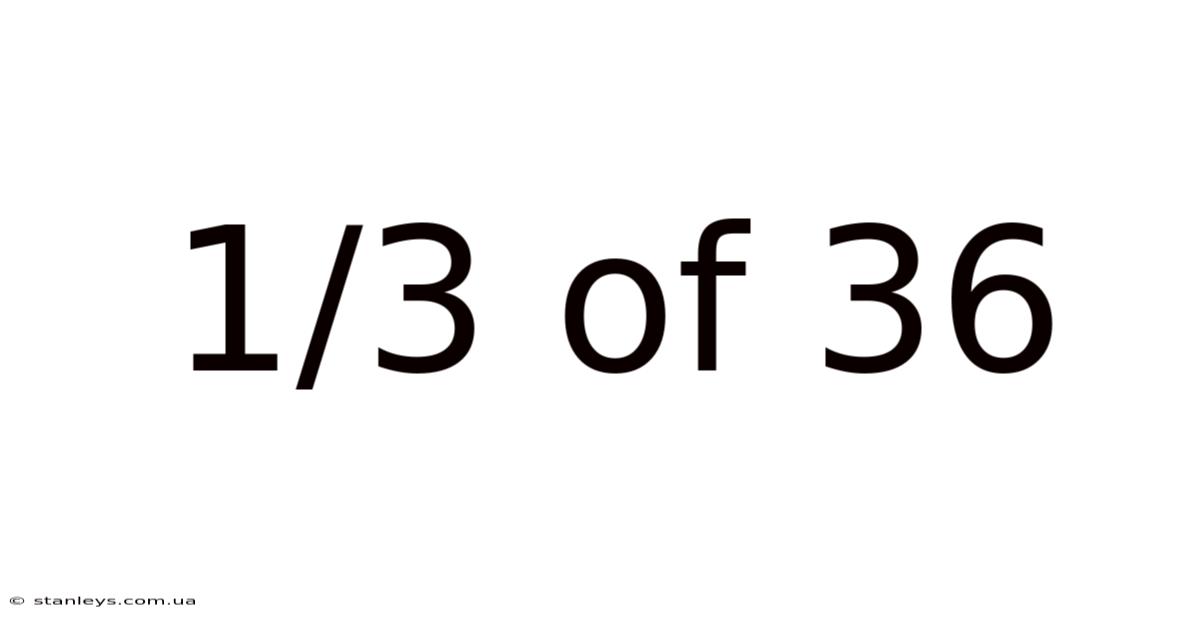
Table of Contents
Decoding 1/3 of 36: A Deep Dive into Fractions and Their Applications
Finding 1/3 of 36 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly basic calculation opens a door to a wider understanding of fractions, their practical applications in everyday life, and even their role in more advanced mathematical concepts. This article will delve into the solution, exploring the underlying principles of fractions, different methods of calculation, and the broader implications of this seemingly simple problem. We will also touch upon real-world scenarios where understanding fractions, and specifically calculating fractions of a whole number, is crucial.
Understanding Fractions: The Building Blocks
Before tackling 1/3 of 36, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In the fraction 1/3, the numerator is 1 and the denominator is 3. This means we are considering one part out of a total of three equal parts. Understanding this fundamental concept is key to solving any fraction-related problem.
Calculating 1/3 of 36: Three Different Approaches
There are several ways to calculate 1/3 of 36. Let's explore three common methods:
1. Division: The most straightforward method involves dividing the whole number (36) by the denominator (3) and then multiplying the result by the numerator (1).
- Step 1: Divide 36 by 3: 36 ÷ 3 = 12
- Step 2: Multiply the result by the numerator (which is 1): 12 x 1 = 12
Therefore, 1/3 of 36 is 12.
2. Multiplication: This method uses the fact that finding a fraction of a number is equivalent to multiplying the number by the fraction.
- Step 1: Convert the whole number 36 into a fraction: 36/1
- Step 2: Multiply the two fractions: (1/3) x (36/1) = (1 x 36) / (3 x 1) = 36/3
- Step 3: Simplify the resulting fraction: 36/3 = 12
Again, we arrive at the answer: 1/3 of 36 is 12.
3. Visual Representation: This method is particularly helpful for visualizing the concept of fractions. Imagine a pizza cut into 3 equal slices. If the whole pizza represents 36, each slice represents 36 ÷ 3 = 12. Since 1/3 represents one slice, 1/3 of 36 is 12. This approach is excellent for beginners as it provides a concrete understanding of the concept.
Expanding the Concept: Fractions and Proportions
The calculation of 1/3 of 36 is not just about finding a part of a whole; it also introduces the concept of proportions. Proportions describe the relationship between two ratios. In this case, the ratio of 1/3 is proportional to the ratio of 12/36. Both ratios represent the same proportion – one-third.
Understanding proportions is crucial in various applications, including:
- Scaling recipes: If a recipe calls for 1/3 cup of sugar, and you want to double the recipe, you'll need to calculate 2/3 of a cup of sugar.
- Map scales: Maps use scales to represent distances. Understanding the scale allows you to calculate the actual distance between two points based on their distance on the map.
- Geometry: Proportions are fundamental to understanding similar shapes and solving geometric problems.
- Engineering: Proportional relationships are critical in designing structures and machines.
Real-World Applications: Where Fractions Matter
Fractions aren't just abstract mathematical concepts; they are essential tools in everyday life. Here are a few examples:
- Shopping: Calculating discounts (e.g., 1/3 off), splitting bills equally among friends, or determining the best value for money based on unit prices.
- Construction: Measuring materials, calculating angles, and determining appropriate proportions for building structures.
- Finance: Understanding interest rates, calculating loan repayments, and analyzing investment returns.
- Cooking: Following recipes accurately requires understanding and using fractions.
- Data Analysis: Understanding percentages and proportions is critical for interpreting data and drawing conclusions from various data sets.
Beyond the Basics: Extending Fraction Knowledge
The seemingly simple problem of finding 1/3 of 36 serves as a springboard for exploring more complex fractional concepts:
- Improper Fractions: Fractions where the numerator is larger than the denominator (e.g., 5/3). These fractions are greater than one whole.
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 1 2/3). This represents a quantity that is more than one whole.
- Equivalent Fractions: Fractions that represent the same value but have different numerators and denominators (e.g., 1/3, 2/6, 3/9).
- Adding, Subtracting, Multiplying, and Dividing Fractions: Mastering these operations is crucial for solving more complex fraction problems.
- Percentages: Percentages are a special type of fraction where the denominator is always 100. Converting fractions to percentages and vice versa is a valuable skill.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 1/3?
A1: 1/3 is already in its simplest form. It cannot be simplified further because the greatest common divisor of 1 and 3 is 1.
Q2: How do I find 2/3 of 36?
A2: You can use the same methods as above. You could divide 36 by 3 (to find 1/3) and then multiply the result by 2. Or you can multiply 36 by 2/3 directly: (2/3) x (36/1) = 72/3 = 24.
Q3: Can I use a calculator to find 1/3 of 36?
A3: Yes, you can. Simply enter 36 x (1/3) or 36 ÷ 3 into your calculator.
Q4: What if I need to find a fraction of a decimal number?
A4: You would follow the same principles. First, convert the decimal into a fraction, then multiply the two fractions.
Conclusion: The Power of Understanding Fractions
The seemingly simple calculation of 1/3 of 36 is a gateway to a much deeper understanding of fractions and their pervasive role in various aspects of life. From everyday tasks like cooking and shopping to more complex applications in engineering and finance, mastering fractions is a fundamental skill. By understanding the underlying principles, exploring various calculation methods, and appreciating their real-world applications, we can unlock the power of fractions and use them effectively to solve problems and make informed decisions. Remember, the seemingly small things, like understanding 1/3 of 36, can build a solid foundation for a more profound mathematical understanding.
Latest Posts
Latest Posts
-
Acetylene Welding Torch
Sep 12, 2025
-
19 5kg In Stone
Sep 12, 2025
-
0 4 In Percentage
Sep 12, 2025
-
76km In Miles
Sep 12, 2025
-
Stock Control System
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1/3 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.