Fully Factorise 12r+16
stanleys
Sep 12, 2025 · 5 min read
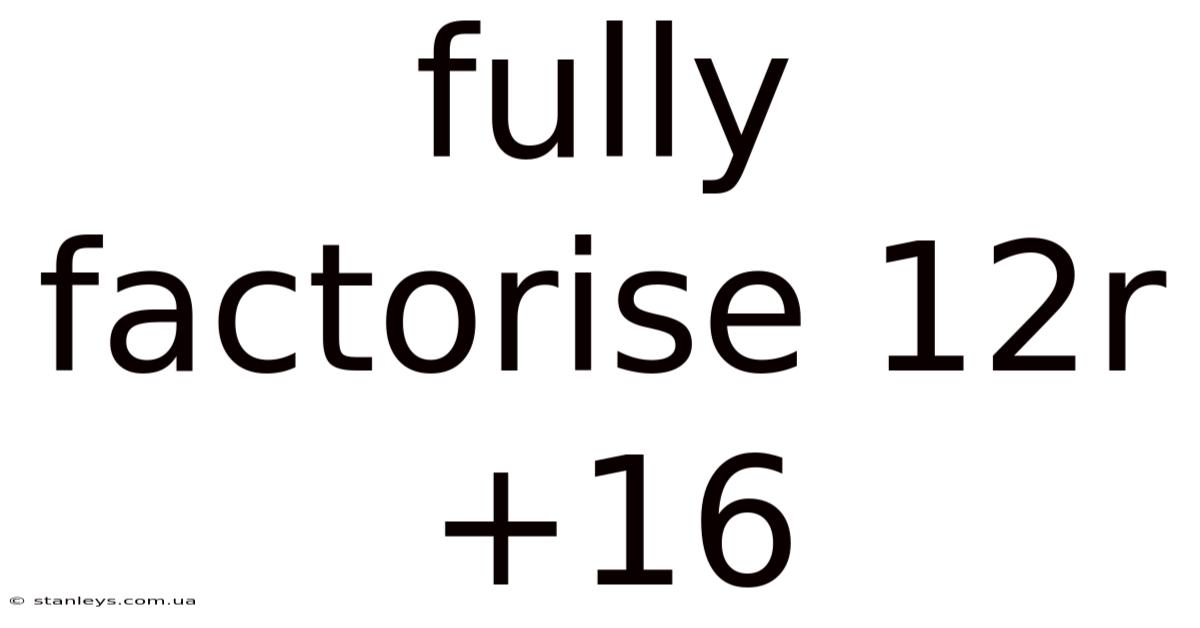
Table of Contents
Fully Factorising Expressions: A Deep Dive into 12r + 16
Fully factorising algebraic expressions is a fundamental skill in algebra. It's the process of breaking down an expression into its simplest multiplicative components. This article will guide you through the process of fully factorising the expression 12r + 16, explaining the steps involved, the underlying mathematical principles, and addressing common questions. We'll explore the concept of highest common factors (HCF) and demonstrate how to apply this to more complex expressions. Understanding this will lay a solid foundation for tackling more advanced algebraic manipulations.
Understanding Factorisation
Before diving into 12r + 16, let's establish a clear understanding of what factorisation means. In essence, factorisation is the reverse process of expanding brackets. When we expand brackets, we multiply terms; when we factorise, we find the common factors that were multiplied together to form the original expression. Consider a simple example: 3(x + 2). Expanding this gives us 3x + 6. Factorising 3x + 6 would bring us back to 3(x + 2).
Finding the Highest Common Factor (HCF)
The key to factorising is identifying the highest common factor (HCF) of the terms within the expression. The HCF is the largest number or term that divides evenly into all the terms in the expression. Let's apply this to 12r + 16.
1. Identify the terms: Our expression has two terms: 12r and 16.
2. Find the factors of each term:
- 12r: The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 'r' are simply 'r' and 1. Therefore, the factors of 12r are 1, 2, 3, 4, 6, 12, r, 2r, 3r, 4r, 6r, and 12r.
- 16: The factors of 16 are 1, 2, 4, 8, and 16.
3. Determine the highest common factor: Looking at the factors of both 12r and 16, we see that the largest number that divides evenly into both is 4. There is no common variable factor (r is only in 12r).
4. Factor out the HCF: Now that we've identified the HCF (4), we factor it out of the expression:
12r + 16 = 4(3r) + 4(4)
Notice that we've divided each term by the HCF (4).
5. Final Factorised Form: We can now rewrite the expression using the distributive property:
12r + 16 = 4(3r + 4)
This is the fully factorised form of 12r + 16. There are no more common factors that can be extracted from the terms inside the brackets.
Expanding the Concept: More Complex Factorisation
While 12r + 16 is a relatively simple example, the principles remain the same for more complex expressions. Let's consider a few examples:
Example 1: 20x² + 15x
-
Identify the terms: 20x² and 15x
-
Find factors:
- 20x²: Factors include 1, 2, 4, 5, 10, 20, x, x², 2x, 4x, 5x, 10x, 20x, 2x², 4x², 5x², 10x², 20x².
- 15x: Factors include 1, 3, 5, 15, x, 3x, 5x, 15x.
-
HCF: The highest common factor is 5x.
-
Factor out the HCF: 20x² + 15x = 5x(4x) + 5x(3)
-
Final Factorised Form: 20x² + 15x = 5x(4x + 3)
Example 2: 18a²b + 27ab²
-
Identify terms: 18a²b and 27ab²
-
Find factors: Consider both numerical and variable factors.
-
HCF: The HCF is 9ab. (9 is the highest common numerical factor, and ab is the highest common variable factor).
-
Factor out the HCF: 18a²b + 27ab² = 9ab(2a) + 9ab(3b)
-
Final Factorised Form: 18a²b + 27ab² = 9ab(2a + 3b)
The Importance of Factorisation
Fully factorising expressions is crucial for several reasons:
- Simplifying expressions: Factorisation simplifies complex expressions, making them easier to understand and manipulate.
- Solving equations: Factorisation is essential for solving quadratic and higher-degree equations.
- Calculus: Factorisation plays a vital role in calculus, particularly in differentiation and integration.
- Problem-solving: Many real-world problems can be modelled using algebraic expressions, and factorisation is often a necessary step in finding solutions.
Frequently Asked Questions (FAQ)
Q1: What if there's no common factor?
If there's no common factor other than 1, the expression is already in its simplest form and cannot be factorised further. For example, 7x + 5y cannot be factorised.
Q2: Can I factorise expressions with more than two terms?
Yes, you can. The principles remain the same. You look for the highest common factor among all the terms. For instance, to factorise 12x³ + 18x² + 6x, the HCF is 6x, resulting in 6x(2x² + 3x + 1).
Q3: What if the expression has negative terms?
Factor out the negative HCF if the terms predominantly share a negative factor. For instance, in -6x - 12, the HCF is -6, so the factorised form is -6(x + 2).
Q4: How do I check my answer?
To verify your factorisation, expand the factorised expression. If you obtain the original expression, your factorisation is correct.
Conclusion
Fully factorising algebraic expressions is a fundamental algebraic skill. The process involves identifying the highest common factor (HCF) of all terms and then extracting that factor. This skill is critical for simplifying expressions, solving equations, and tackling more advanced mathematical concepts. By understanding the underlying principles and practicing with various examples, you can master this essential skill and build a strong foundation for your further studies in mathematics. Remember, practice is key! Work through various examples, gradually increasing the complexity of the expressions you factorise. With consistent effort, you'll develop confidence and proficiency in this vital area of algebra.
Latest Posts
Latest Posts
-
81kg In Lb
Sep 12, 2025
-
42kg In Lbs
Sep 12, 2025
-
1 3 Of 36
Sep 12, 2025
-
Dl I Liter
Sep 12, 2025
-
115lbs To Kg
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Fully Factorise 12r+16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.