Cos 25 Degrees
stanleys
Sep 17, 2025 · 6 min read
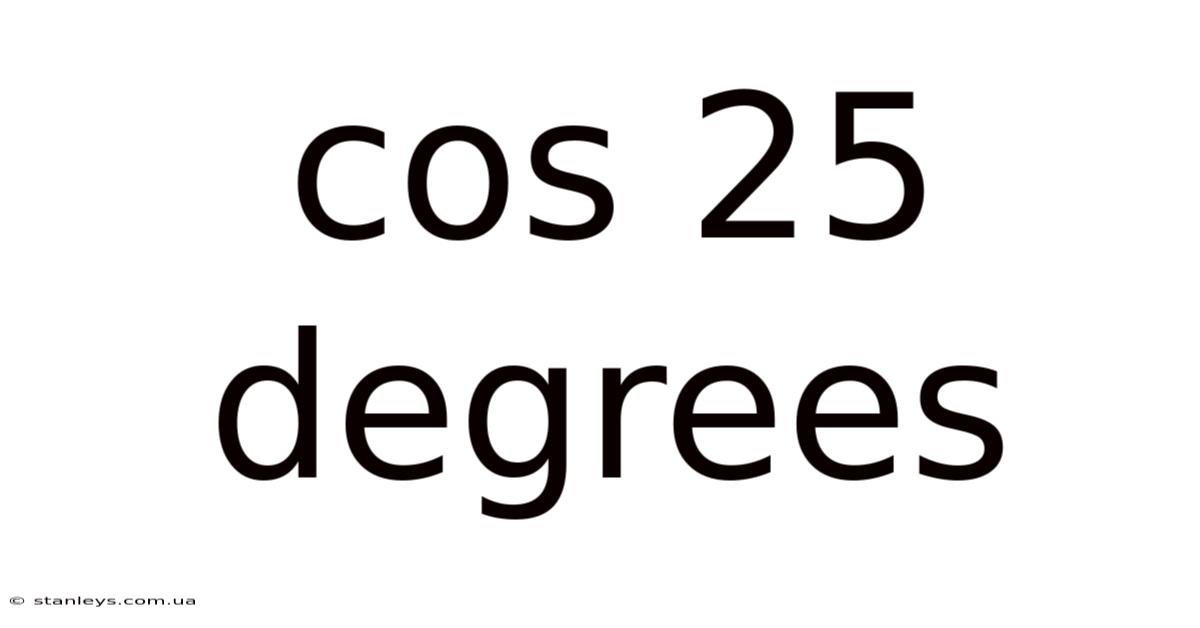
Table of Contents
Decoding cos 25°: A Deep Dive into Trigonometry
Understanding the cosine of 25 degrees (cos 25°) might seem like a simple trigonometric problem, but it opens a door to a fascinating world of mathematical concepts and their applications. This article will explore cos 25° in detail, moving beyond a simple calculator answer to unravel the underlying principles, practical applications, and related concepts. We'll delve into methods for calculating it, its significance in various fields, and answer frequently asked questions. This comprehensive guide will equip you with a thorough understanding of cos 25° and its place within the broader landscape of trigonometry.
Introduction to Cosine and Angles
Before jumping into the specifics of cos 25°, let's refresh our understanding of cosine. In a right-angled triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. This ratio remains constant for a given angle, regardless of the size of the triangle. The angle is typically measured in degrees or radians. Cosine, along with sine and tangent, forms the foundation of trigonometry, a branch of mathematics crucial for understanding periodic functions and spatial relationships.
The unit circle provides a powerful visual representation. Imagine a circle with a radius of 1. Starting at the point (1,0), we move counterclockwise along the circle. The x-coordinate of the point where the angle intersects the circle represents the cosine of that angle. For 25°, this point lies in the first quadrant, indicating a positive cosine value.
Calculating cos 25°: Methods and Approximations
Calculating the exact value of cos 25° is not straightforward. Unlike angles like 0°, 30°, 45°, 60°, and 90°, which have simple, exact trigonometric ratios, 25° doesn't yield a neat radical expression. We need to employ approximation methods.
-
Using a Calculator: The most common and simplest approach is using a scientific calculator. Simply input "cos(25)" (ensuring your calculator is set to degrees mode), and you'll get an approximate value of 0.9063.
-
Taylor Series Expansion: For a more precise understanding, we can leverage the Taylor series expansion for cosine:
cos(x) = 1 - x²/2! + x⁴/4! - x⁶/6! + ...
where x is the angle in radians. First, convert 25° to radians:
25° * (π/180°) ≈ 0.4363 radians
Substituting this value into the Taylor series, and adding more terms for increased accuracy, we obtain a very close approximation of cos 25°. However, this method requires significant computation, especially for higher levels of accuracy.
-
Half-Angle Formulas: Trigonometric identities, such as half-angle formulas, can be used to express cos 25° in terms of other known trigonometric values. While this approach might seem complex initially, it highlights the interconnectedness of trigonometric functions and offers a deeper mathematical understanding. However, it ultimately still leads to an approximation, as it often relies on values that themselves are approximated.
-
Numerical Methods: Sophisticated numerical methods like Newton-Raphson iteration can provide highly accurate approximations. These methods are typically implemented using computer programs and are beyond the scope of manual calculation.
The Significance of cos 25° in Various Fields
While it may seem like a specific and isolated value, cos 25° plays a role in various applications:
-
Engineering and Physics: Cosine is fundamental in calculating forces, velocities, and displacements in various systems. For instance, in analyzing projectile motion, the horizontal component of velocity involves cosine. Any problem involving an angle of 25° will necessitate the use of its cosine value.
-
Computer Graphics and Game Development: In rendering three-dimensional graphics and simulating realistic movement, cosine is crucial for transforming coordinates and calculating angles. The precise calculation of angles is essential for realistic visuals and character animations.
-
Navigation and Surveying: Determining distances and bearings often involves trigonometric calculations. Cosine helps solve problems related to triangulation and determining positions based on angles and known distances.
-
Signal Processing and Electronics: Cosine functions are integral to representing and analyzing periodic signals and waves. In the frequency domain, cosine transformations are essential.
-
Astronomy and Astrophysics: Calculating orbits, positions of celestial bodies, and distances in astronomy extensively involves trigonometric functions, including cosine. The study of stellar motion and orbital mechanics requires precise trigonometric calculations.
Understanding the Unit Circle and its Relation to cos 25°
The unit circle provides a visual and intuitive way to understand trigonometric functions. As mentioned earlier, the x-coordinate of the point where the 25° angle intersects the unit circle gives us the value of cos 25°. This visualization is particularly helpful in understanding the relationships between different trigonometric functions and their values across different quadrants.
The first quadrant (where 25° lies) is characterized by positive values for both sine and cosine. Understanding the unit circle clarifies why cos 25° is positive. It also helps in grasping the behavior of cosine for angles greater than 90°, as the x-coordinate will become negative in the second and third quadrants.
Exploring Related Trigonometric Concepts
Understanding cos 25° necessitates familiarity with related concepts:
-
Sine (sin 25°): The sine of 25° represents the y-coordinate on the unit circle. Both sin 25° and cos 25° are related through the Pythagorean identity: sin²θ + cos²θ = 1.
-
Tangent (tan 25°): The tangent of 25° is the ratio of sin 25° to cos 25°. Understanding the tangent function allows for a complete grasp of the trigonometric functions related to the angle.
-
Inverse Trigonometric Functions: These functions (arccos, arcsin, arctan) provide the angle given the trigonometric ratio. For example, arccos(0.9063) ≈ 25°.
-
Trigonometric Identities: These are equations that are true for all angles. They are fundamental to simplifying complex trigonometric expressions and solving trigonometric equations. Many identities relate cosine to sine and tangent.
Frequently Asked Questions (FAQ)
-
Q: Is cos 25° a rational number?
- A: No, cos 25° is an irrational number. It cannot be expressed as a simple fraction of two integers. This is true for most angles besides special angles like 0°, 30°, 45°, 60°, and 90°.
-
Q: How accurate does the approximation of cos 25° need to be for most applications?
- A: The required accuracy depends heavily on the application. For many engineering and physics problems, the approximation provided by a standard calculator (around 0.9063) is sufficient. However, applications requiring extremely high precision, like satellite navigation or advanced simulations, demand much more accurate approximations.
-
Q: Can I use the angle sum or difference identities to calculate cos 25°?
- A: While you can try to use angle sum or difference identities, this approach typically leads to a chain of approximations that might not improve the overall accuracy significantly. This is because the process often involves using trigonometric functions of angles that themselves lack exact values.
-
Q: What programming languages or software can be used to calculate cos 25° with high accuracy?
- A: Many programming languages (Python, MATLAB, C++, etc.) have built-in functions for calculating trigonometric functions with high precision. Specialized mathematical software packages offer even greater accuracy and computational power.
Conclusion
Cos 25° might initially seem like a simple value, but its calculation and significance reveal the rich depth and practical application of trigonometry. From understanding basic trigonometric ratios to using advanced computational methods, this exploration has demonstrated the versatility of cosine and its crucial role across diverse scientific and technological disciplines. The methods discussed, along with the conceptual understanding provided, will help you grasp not only the specific value of cos 25° but also the underlying principles that make it a vital part of mathematics and its applications in the world around us. Remember, even seemingly simple values can unveil a profound understanding of the intricate world of mathematics.
Latest Posts
Latest Posts
-
Test In Spanish
Sep 17, 2025
-
1 55kg To Lbs
Sep 17, 2025
-
Microns To Millimeters
Sep 17, 2025
-
180grams To Oz
Sep 17, 2025
-
28 Times 5
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Cos 25 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.