96 Divided 6
stanleys
Sep 11, 2025 · 6 min read
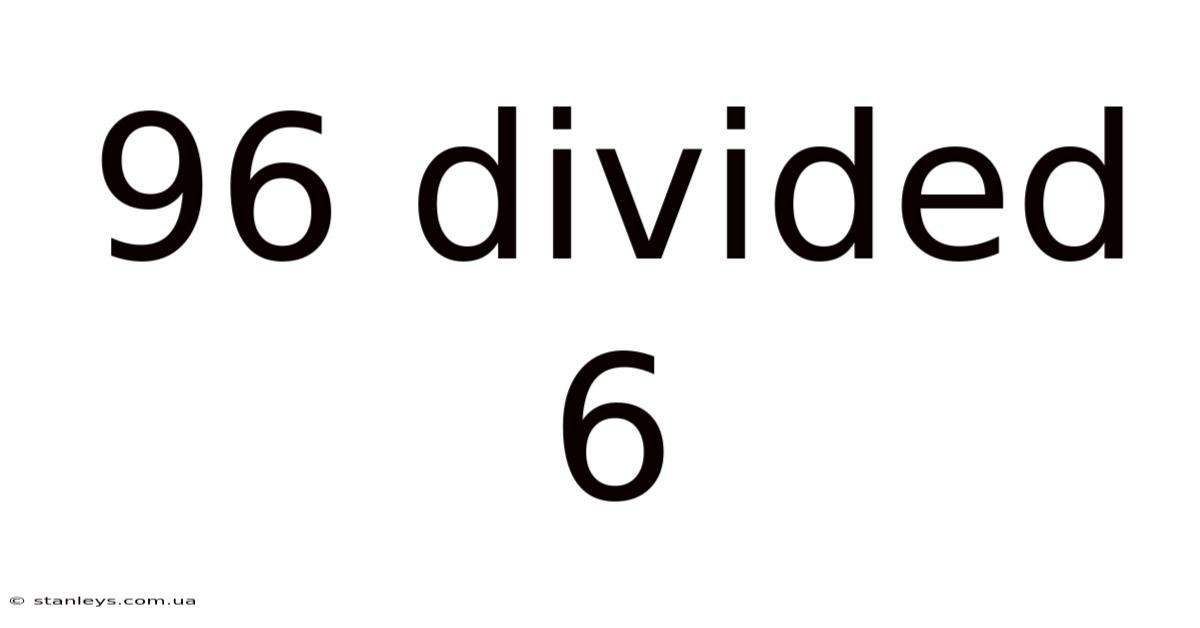
Table of Contents
96 Divided by 6: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 96 divided by 6, but goes far beyond a mere answer. We'll delve into the fundamentals of division, explore different methods of solving this problem, examine its practical applications in various fields, and even touch upon the historical context of division as a mathematical operation. Understanding this seemingly basic calculation unlocks a deeper understanding of mathematical principles and their real-world relevance.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the inverse of multiplication. While multiplication combines groups of equal size, division separates a quantity into equal groups. In the context of "96 divided by 6," we're asking: "How many times does 6 fit into 96?" The answer, the quotient, represents the number of equal groups, while any remainder represents the amount left over after the equal groups have been formed.
Methods for Solving 96 ÷ 6
There are several ways to solve 96 divided by 6. Let's explore a few common approaches:
1. Long Division: A Step-by-Step Approach
Long division is a systematic method ideal for larger numbers. Here's how to solve 96 ÷ 6 using long division:
-
Set up the problem: Write 96 inside the long division symbol (⟌) and 6 outside.
-
Divide the tens: How many times does 6 go into 9? It goes once (1). Write the 1 above the 9.
-
Multiply and subtract: Multiply the 1 by 6 (1 x 6 = 6). Subtract this from 9 (9 - 6 = 3).
-
Bring down the ones: Bring down the 6 from the ones place next to the 3, making it 36.
-
Divide the ones: How many times does 6 go into 36? It goes six times (6). Write the 6 above the 6 in 96.
-
Multiply and subtract: Multiply the 6 by 6 (6 x 6 = 36). Subtract this from 36 (36 - 36 = 0).
-
The quotient: The number above the division symbol (16) is the quotient. Therefore, 96 ÷ 6 = 16.
2. Repeated Subtraction: A Conceptual Approach
This method is excellent for visualizing the concept of division. We repeatedly subtract 6 from 96 until we reach 0:
96 - 6 = 90 90 - 6 = 84 84 - 6 = 78 ...and so on.
Counting how many times you subtract 6 will give you the quotient (16). While effective for smaller numbers, this method becomes cumbersome with larger numbers.
3. Multiplication: Using Inverse Operations
Since division is the inverse of multiplication, we can find the answer by asking: "What number multiplied by 6 equals 96?" Through trial and error or knowledge of multiplication tables, we arrive at 16 (16 x 6 = 96). This method is quicker for those comfortable with multiplication facts.
4. Factoring: Breaking Down the Numbers
We can factor both 96 and 6 into their prime factors:
- 96 = 2 x 2 x 2 x 2 x 2 x 3
- 6 = 2 x 3
By canceling out common factors (2 and 3), we are left with 2 x 2 x 2 x 2 = 16. This demonstrates that 6 goes into 96 sixteen times. This approach is beneficial for understanding the underlying structure of the numbers involved.
Real-World Applications of Division: Beyond the Classroom
The seemingly simple calculation of 96 ÷ 6 has numerous practical applications in everyday life and various professional fields:
-
Equal Sharing: Dividing 96 candies amongst 6 friends results in each friend receiving 16 candies. This is a fundamental application of division encountered frequently in daily life.
-
Rate and Speed: If a car travels 96 miles in 6 hours, its average speed is 16 miles per hour (96 miles ÷ 6 hours = 16 mph). This highlights the use of division in calculating rates and speeds.
-
Unit Conversion: Converting units often involves division. For example, if you have 96 inches and need to convert to feet (1 foot = 12 inches), you would divide 96 by 12 to get 8 feet.
-
Data Analysis: In statistics and data analysis, division is crucial for calculating averages, percentages, and ratios. For instance, determining the average score on a test involving 6 students and a total score of 96 points would involve division (96 points ÷ 6 students = 16 points/student).
-
Engineering and Construction: Calculating material requirements, distributing loads, and determining dimensions frequently involve division in engineering and construction projects.
-
Finance and Accounting: Calculating unit costs, profit margins, and interest rates all rely on division. For example, dividing total profit by the number of units sold determines profit per unit.
-
Computer Science: Division is a fundamental operation in computer programming used in numerous algorithms and calculations.
Expanding the Concept: Division with Remainders
While 96 ÷ 6 results in a whole number (16), not all division problems yield such neat results. Consider a scenario where we have 97 items to divide among 6 people. Using long division:
- 6 goes into 9 once (1).
- 9 - 6 = 3.
- Bring down the 7, making 37.
- 6 goes into 37 six times (6).
- 37 - 36 = 1.
The quotient is 16, and the remainder is 1. This means each person gets 16 items, and there's 1 item left over. Understanding remainders is essential in many real-world applications, such as distributing resources or scheduling tasks.
Frequently Asked Questions (FAQ)
Q: What is the simplest way to divide 96 by 6?
A: The simplest way depends on your comfort level with multiplication tables. If you know that 6 x 16 = 96, then you instantly know that 96 ÷ 6 = 16. Otherwise, long division provides a systematic approach.
Q: Can I use a calculator to solve 96 ÷ 6?
A: Absolutely! Calculators are valuable tools for solving mathematical problems, especially larger or more complex ones.
Q: What if I get a decimal answer when dividing?
A: A decimal answer indicates that the division doesn't result in a whole number. This often occurs when the numerator (top number) isn't perfectly divisible by the denominator (bottom number). The decimal represents the fractional part of the quotient.
Q: Why is understanding division important?
A: Division is a fundamental mathematical concept used extensively in everyday life, various professions, and advanced mathematical studies. Mastering division is crucial for problem-solving and critical thinking skills.
Conclusion: The Power of a Simple Calculation
The seemingly simple problem of 96 divided by 6 illustrates the power and versatility of division as a fundamental mathematical operation. While the answer, 16, is straightforward, the process of arriving at that answer, and the understanding of the underlying principles, opens up a world of applications and further mathematical exploration. From everyday tasks to complex scientific calculations, division forms the basis of numerous problem-solving strategies and helps us understand and interact with the world around us. Mastering this fundamental operation empowers you with a crucial tool for navigating various aspects of life and learning.
Latest Posts
Latest Posts
-
1 66m In Ft
Sep 11, 2025
-
Stop In Latin
Sep 11, 2025
-
40 Of 10000
Sep 11, 2025
-
Flow God Reed
Sep 11, 2025
-
80mm In Cm
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 96 Divided 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.