40 Of 10000
stanleys
Sep 11, 2025 · 6 min read
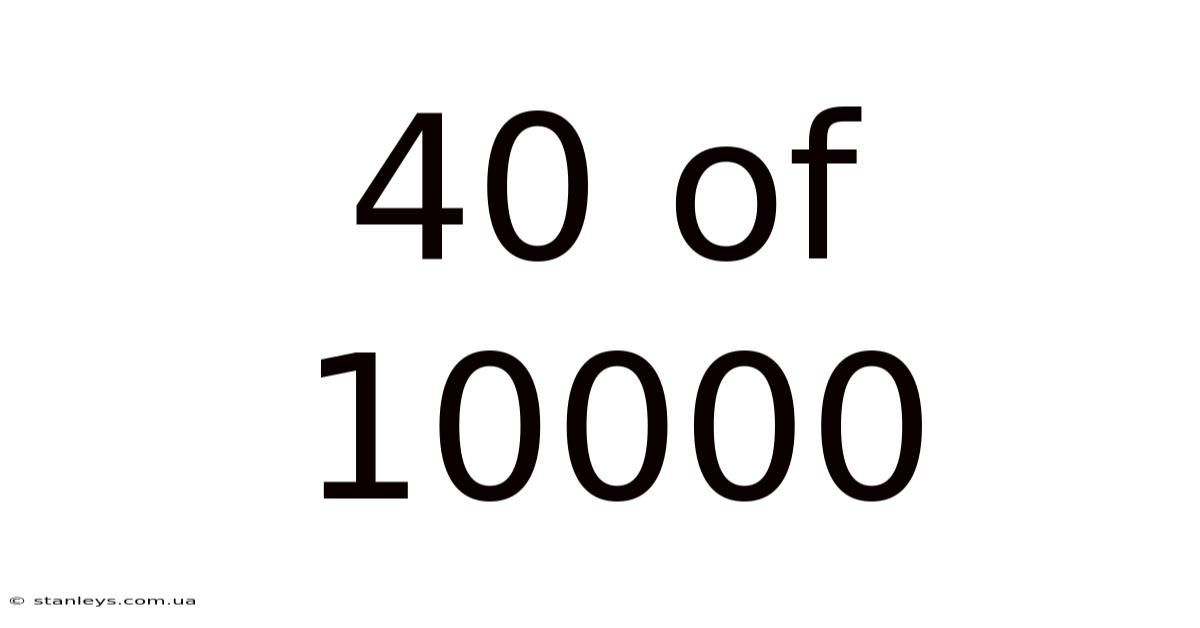
Table of Contents
Decoding 40/10000: A Deep Dive into Percentages, Probabilities, and Practical Applications
Understanding the seemingly simple fraction 40/10000, or its decimal equivalent 0.004, unlocks a gateway to comprehending percentages, probabilities, and their wide-ranging applications in various fields. This seemingly insignificant number can represent a crucial piece of data in scenarios from financial markets to medical research, from quality control to climate science. This article will explore the meaning of 40/10000, delve into its implications in different contexts, and examine the broader mathematical concepts it embodies.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the specifics of 40/10000, let's solidify our understanding of the fundamental building blocks: fractions, decimals, and percentages.
A fraction represents a part of a whole. 40/10000 signifies 40 parts out of a total of 10000 parts.
A decimal is another way to represent a fraction, using a base-ten system. 40/10000 is equivalent to 0.004. This decimal representation makes it easier to compare and perform calculations with other numbers.
A percentage expresses a fraction or decimal as a proportion of 100. To convert 40/10000 to a percentage, we multiply by 100%: (40/10000) * 100% = 0.4%. This means 40 out of 10000 represents 0.4% of the total.
Interpreting 40/10000 in Different Contexts
The interpretation of 40/10000 heavily depends on the context in which it's used. Let's explore a few examples:
-
Financial Markets: In the stock market, 40/10000 could represent the change in a stock's price. A 0.4% decrease might seem negligible, but over time, these small changes can accumulate significantly, impacting overall portfolio value. Consider a scenario where 40 out of 10000 shares were sold, indicating a relatively small transaction compared to the total volume.
-
Quality Control: In manufacturing, 40 defective items out of 10000 produced indicates a defect rate of 0.4%. While seemingly low, this percentage might still be unacceptable for certain products, triggering investigations into the production process to improve quality control and reduce defects. Depending on industry standards and the potential consequences of product failure, even a 0.4% defect rate might be cause for concern.
-
Medical Research: In clinical trials, 40 positive results out of 10000 participants might indicate the efficacy of a new treatment. This success rate of 0.4% might be analyzed in conjunction with other clinical data, such as side effects and placebo responses, to determine the true effectiveness and safety of the treatment. Analyzing statistical significance is crucial here to understand if this result is truly significant or just random chance.
-
Environmental Science: In environmental monitoring, 40 polluted samples out of 10000 might represent a contamination level of 0.4%. This relatively low percentage might still be significant, depending on the type and concentration of pollutants, and might trigger further investigation and remediation efforts. The context, including the severity of the pollution, is vital for interpretation.
-
Social Sciences: Imagine a survey with 10000 respondents; 40 participants responding in a specific way represent 0.4% of the total sample. Whether this is considered significant or not depends on the margin of error, confidence intervals, and the specific research question.
Probability and Statistical Significance
The fraction 40/10000 can also be viewed through the lens of probability. The probability of an event occurring is often expressed as a fraction, decimal, or percentage. In this case, 40/10000 represents the probability of a specific event occurring in a sample of 10000. Determining if this probability is statistically significant requires considering factors like the expected probability (based on existing knowledge) and the margin of error.
For example, in a coin toss experiment, the probability of getting heads is 50%, or 0.5. If we observe 40 heads in 10000 tosses, the observed probability is 0.4%, which is significantly different from the expected probability. Statistical tests can determine whether this difference is due to random chance or indicates a bias in the coin or the tossing process.
Expanding the Understanding: Proportions and Ratios
The concept extends beyond simple probabilities. The ratio 40:10000 describes the proportional relationship between two quantities. This ratio can be simplified to 1:250, highlighting that for every one instance of the event, there are 250 instances where it does not occur. Understanding ratios and proportions helps in scaling up or down calculations and predictions.
Calculations and Applications: Real-World Examples
Let's look at some practical applications of calculating with 40/10000:
-
Calculating percentages: To calculate 0.4% of a larger number (e.g., calculating a 0.4% discount on a $1000 purchase), simply multiply the larger number by 0.004. In this case, the discount would be $4.
-
Estimating populations: If 0.4% of a larger population exhibits a certain characteristic, we can estimate the size of the total population. For example, if 40 people out of 10000 have a specific genetic trait, we can extrapolate this to estimate the prevalence of that trait in a larger population.
-
Comparing proportions: We can compare 40/10000 to other proportions to assess relative magnitudes. For instance, if another group shows a higher or lower percentage, we can determine the significance of the differences.
Frequently Asked Questions (FAQ)
-
Q: How do I convert 40/10000 to a decimal?
- A: Divide 40 by 10000: 40 ÷ 10000 = 0.004
-
Q: How do I convert 40/10000 to a percentage?
- A: Multiply the decimal (0.004) by 100: 0.004 * 100 = 0.4%
-
Q: Is 0.4% a significant number?
- A: The significance of 0.4% depends entirely on the context. In some situations, it might be negligible, while in others, it could be highly significant.
-
Q: How can I use 40/10000 in statistical analysis?
- A: You would use 40/10000 as the observed proportion or probability in various statistical tests, such as hypothesis testing, to determine if there's a statistically significant difference from an expected value or another group.
-
Q: What are the limitations of using 40/10000?
- A: The main limitation is the small sample size. While 10000 might seem like a large number, in some situations it might not be sufficient to draw robust conclusions, especially when dealing with rare events. Larger sample sizes would generally lead to more reliable results.
Conclusion: The Power of Small Numbers
The seemingly insignificant fraction 40/10000 holds significant meaning in numerous applications. Understanding its representation as a decimal (0.004) and percentage (0.4%) allows us to interpret it within various contexts, from finance and manufacturing to medicine and environmental science. By mastering the fundamentals of fractions, decimals, percentages, probabilities, and statistical significance, we unlock the power of these seemingly small numbers to reveal critical information and insights in the world around us. Remember that the importance of a number isn’t solely determined by its magnitude but by its meaning within a specific context. Learning to interpret and analyze these values is crucial for making informed decisions in diverse fields.
Latest Posts
Latest Posts
-
0 75 X 3
Sep 11, 2025
-
127lbs To Kg
Sep 11, 2025
-
1000 Times 1000
Sep 11, 2025
-
52f To Celsius
Sep 11, 2025
-
22kg To Lbs
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 10000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.