9/20 Of 540
stanleys
Sep 13, 2025 · 5 min read
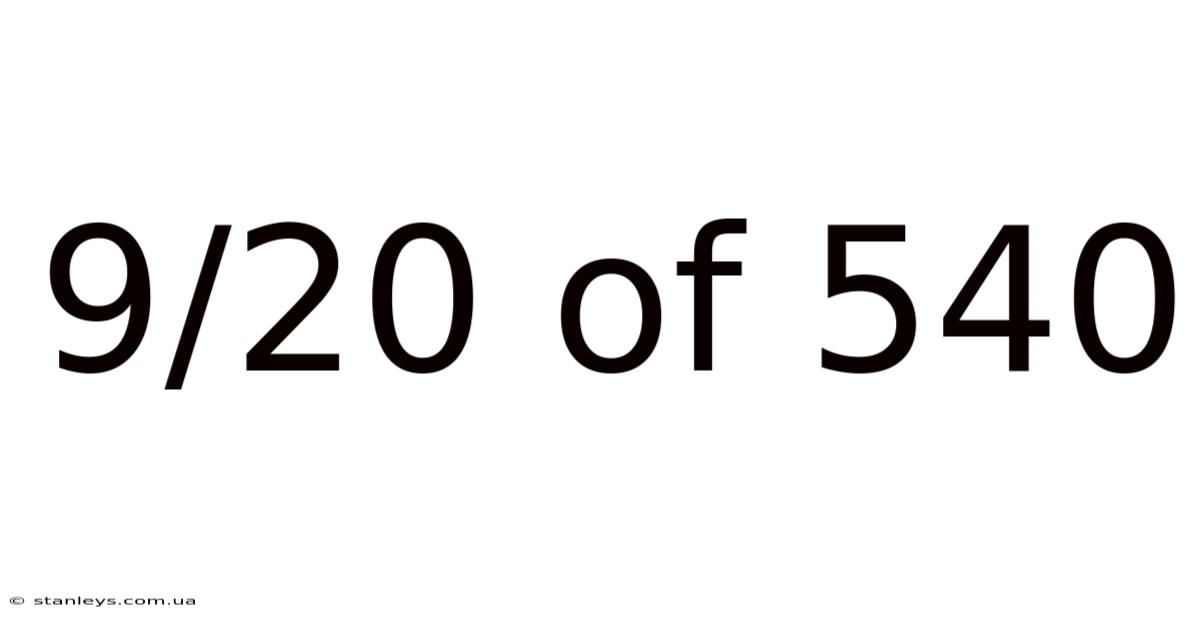
Table of Contents
Decoding 9/20 of 540: A Comprehensive Guide to Fractions and Proportions
Finding 9/20 of 540 might seem like a simple math problem at first glance. However, understanding the underlying concepts of fractions and proportions opens up a world of applications beyond this single calculation. This article will delve deep into solving this specific problem, explaining the various methods, exploring the theoretical underpinnings, and providing a broader context for understanding fractions and their role in everyday life. We'll cover different approaches, including using decimals, and address common misconceptions. By the end, you'll not only know the answer but also possess a more robust understanding of fractional arithmetic.
Understanding the Problem: 9/20 of 540
The phrase "9/20 of 540" translates mathematically to a multiplication problem: (9/20) * 540. This involves finding a fraction (9/20) of a whole number (540). This type of problem frequently appears in various contexts, from calculating discounts and percentages to determining proportions in recipes and understanding data representation.
Method 1: Direct Multiplication
The most straightforward approach involves directly multiplying the fraction by the whole number.
-
Step 1: Convert the whole number into a fraction: We can rewrite 540 as 540/1. This doesn't change its value but makes the multiplication easier.
-
Step 2: Multiply the numerators and denominators: Multiply the numerators (top numbers) together and the denominators (bottom numbers) together: (9 * 540) / (20 * 1) = 4860 / 20
-
Step 3: Simplify the fraction: Now we simplify the resulting fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 4860 and 20 is 20. Therefore: 4860 / 20 = 243
Therefore, 9/20 of 540 is 243.
Method 2: Simplifying Before Multiplication
This method involves simplifying the fraction before performing the multiplication. This can often make the calculation easier, especially with larger numbers.
-
Step 1: Simplify the fraction: Notice that both 20 and 540 are divisible by 10. If we divide both the numerator and the denominator of 9/20 by 10, it becomes 9/2. Further simplification isn't possible.
-
Step 2: Multiply the simplified fraction by the whole number: Now multiply (9/2) * 540. This can be written as (9 * 540) / 2 = 4860/2
-
Step 3: Perform the division: 4860 / 2 = 243
Again, we arrive at the answer: 243.
Method 3: Using Decimals
Converting the fraction to a decimal can also be a useful approach.
-
Step 1: Convert the fraction to a decimal: Divide the numerator (9) by the denominator (20): 9 ÷ 20 = 0.45
-
Step 2: Multiply the decimal by the whole number: Multiply the decimal (0.45) by the whole number (540): 0.45 * 540 = 243
This method provides the same answer: 243.
Method 4: Proportionality and Cross-Multiplication
This approach uses the concept of proportions. We can set up a proportion:
9/20 = x/540
where 'x' represents the unknown value (9/20 of 540).
To solve for 'x', we cross-multiply:
9 * 540 = 20 * x
4860 = 20x
Now, divide both sides by 20:
x = 4860 / 20 = 243
The solution remains: 243.
The Significance of Fractions and Proportions
The seemingly simple problem of finding 9/20 of 540 highlights the importance of understanding fractions and proportions. These concepts are fundamental to various areas:
-
Percentage Calculations: Percentages are simply fractions expressed as parts of 100. Understanding fractions allows for easy conversion between fractions, decimals, and percentages. For instance, 9/20 is equivalent to 45% (9/20 * 100 = 45).
-
Ratio and Proportion Problems: Many real-world problems involve ratios and proportions. These include scaling recipes, calculating fuel efficiency, understanding population demographics, and analyzing financial data.
-
Geometry and Measurement: Fractions are crucial in geometry for calculating areas, volumes, and lengths of shapes.
-
Data Analysis: Fractions and percentages are used extensively in representing and interpreting data in charts, graphs, and statistical analyses.
-
Everyday Life: From splitting bills fairly among friends to understanding sale discounts in stores, fractions are integral to everyday life.
Common Mistakes and Misconceptions
-
Incorrect Order of Operations: Always remember the order of operations (PEMDAS/BODMAS). Multiplication and division should be performed before addition and subtraction.
-
Incorrect Simplification of Fractions: Ensure that you simplify fractions correctly by dividing the numerator and denominator by their greatest common divisor.
-
Decimal Place Errors: When using decimal conversions, be mindful of the decimal place to avoid calculation errors.
-
Confusion with Percentage: Don't confuse fractions directly with percentages without making the appropriate conversion.
Frequently Asked Questions (FAQs)
-
What is the simplest form of 9/20? 9/20 is already in its simplest form because 9 and 20 share no common factors other than 1.
-
Can I solve this using a calculator? Yes, you can directly input (9/20) * 540 into a calculator to obtain the answer.
-
What if the fraction was a mixed number? If the fraction were a mixed number (e.g., 1 9/20), you would first convert it to an improper fraction before proceeding with the multiplication.
-
How can I improve my understanding of fractions? Practice solving various fraction problems, focusing on different methods. Use visual aids like diagrams or fraction bars to build a stronger intuitive grasp.
Conclusion: Beyond the Calculation
Solving "9/20 of 540" is more than just finding the answer (243). It's an opportunity to strengthen your understanding of fractions, proportions, and their widespread applications. Mastering these fundamental concepts empowers you to confidently tackle more complex mathematical problems and successfully navigate numerous real-world scenarios. By understanding the different methods, identifying common pitfalls, and appreciating the broader context, you've not only solved a problem but gained a deeper insight into a cornerstone of mathematics. The journey of understanding is as important as the destination itself, and this exploration into the seemingly simple calculation offers a valuable lesson in mathematical literacy.
Latest Posts
Latest Posts
-
124 Lbs Kg
Sep 13, 2025
-
76f To C
Sep 13, 2025
-
30 X 10
Sep 13, 2025
-
Two Strand Locs
Sep 13, 2025
-
105f In C
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 9/20 Of 540 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.