30 X 10
stanleys
Sep 13, 2025 · 6 min read
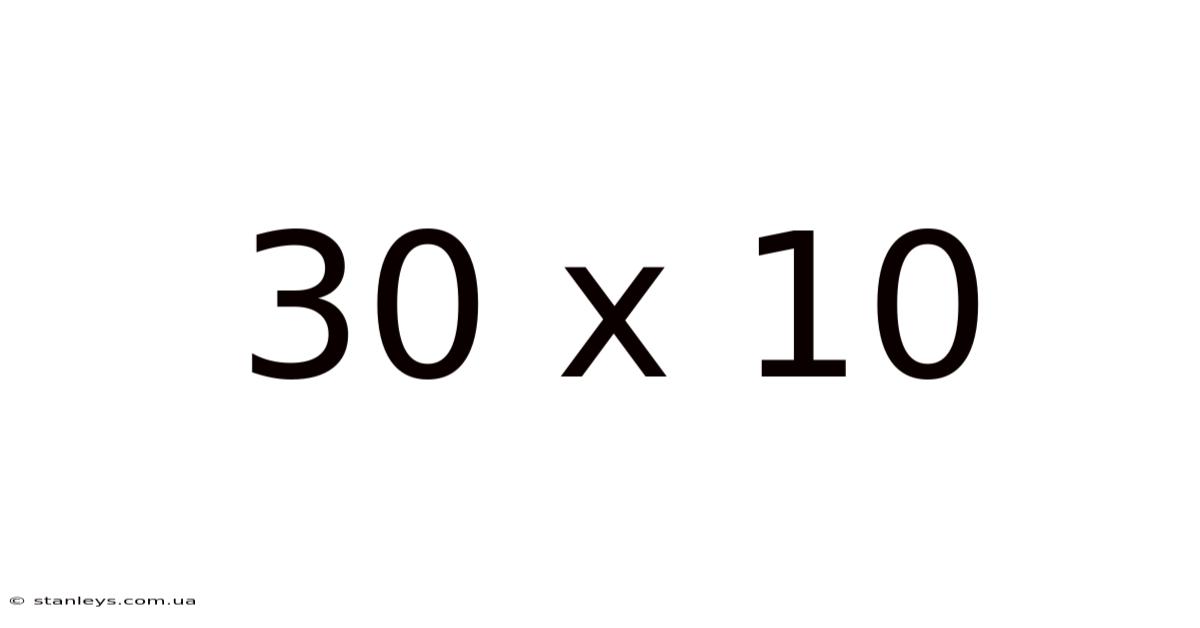
Table of Contents
Decoding 30 x 10: Exploring Multiplication, Area, and Beyond
This article delves into the seemingly simple calculation of 30 x 10, exploring its various interpretations and applications beyond basic arithmetic. We'll unravel the underlying mathematical principles, connect it to real-world scenarios, and examine how this seemingly straightforward equation can serve as a foundational concept for understanding more complex mathematical ideas. Whether you're a student brushing up on multiplication or an adult seeking to strengthen your numeracy skills, this comprehensive guide will provide a rich and rewarding learning experience.
Understanding Basic Multiplication: The Fundamentals of 30 x 10
At its core, 30 x 10 represents a multiplication problem. Multiplication is a fundamental arithmetic operation that essentially involves repeated addition. In this case, 30 x 10 means adding the number 30 ten times: 30 + 30 + 30 + 30 + 30 + 30 + 30 + 30 + 30 + 30. The result, as we all know, is 300. This simple equation forms the bedrock of numerous mathematical concepts and practical applications.
Understanding the factors: The numbers 30 and 10 are known as factors in this multiplication problem. Understanding the factors is crucial for grasping the concept of multiplication and its various applications. 30 can be broken down into its prime factors (2 x 3 x 5), while 10 is (2 x 5). This prime factorization helps in simplifying calculations and understanding the relationships between numbers.
Commutative Property: It's important to note the commutative property of multiplication, which states that the order of the factors does not affect the product. Therefore, 30 x 10 is the same as 10 x 30, both equaling 300. This property simplifies calculations and allows for flexibility in approaching multiplication problems.
Visualizing 30 x 10: The Concept of Area
A powerful way to visualize 30 x 10 is through the concept of area. Imagine a rectangle with a length of 30 units and a width of 10 units. The area of this rectangle is calculated by multiplying its length and width: 30 units x 10 units = 300 square units. This visual representation makes the concept of multiplication more concrete and relatable, especially for visual learners. This connection between multiplication and area extends to various real-world applications, from calculating the size of rooms to determining the surface area of objects.
This visual approach helps to solidify the understanding of multiplication beyond just rote memorization. It allows for a deeper understanding of the relationship between dimensions and area, a fundamental concept in geometry and numerous other fields.
Real-World Applications: From Everyday Life to Advanced Concepts
The seemingly simple equation 30 x 10 finds its application in numerous real-world scenarios, highlighting its practical importance:
-
Calculating Costs: Imagine buying 10 items that cost $30 each. The total cost would be 30 x 10 = $300. This simple calculation is essential for budgeting, shopping, and financial planning.
-
Measuring Distances: If you travel at a speed of 30 km/hour for 10 hours, the total distance covered would be 30 x 10 = 300 km. This is a fundamental calculation in physics and transportation.
-
Determining Quantities: If you have 10 boxes, each containing 30 apples, the total number of apples would be 30 x 10 = 300. This simple calculation is crucial in inventory management and logistics.
-
Scaling and Proportions: Understanding 30 x 10 helps in grasping the concept of scaling and proportions. For instance, if a recipe calls for 10 units of an ingredient and you need to make it three times larger, you would multiply the quantity by 30, resulting in 300 units.
-
Data Analysis and Statistics: In data analysis and statistics, multiplication is frequently used to calculate totals, averages, and percentages. Understanding fundamental multiplication like 30 x 10 is crucial for performing these calculations accurately.
Extending the Concept: Exploring Larger Numbers and Advanced Multiplication Techniques
The foundation laid by understanding 30 x 10 can be extended to tackling more complex multiplication problems. By understanding the distributive property, we can break down larger numbers into smaller, more manageable components. For example, multiplying 30 x 105 can be simplified as 30 x (100 + 5) = (30 x 100) + (30 x 5) = 3000 + 150 = 3150. This technique makes complex calculations less daunting and more efficient.
Similarly, understanding place value is crucial for multiplying larger numbers. Recognizing that 30 is equivalent to 3 tens and 10 is equivalent to 1 ten allows for a more intuitive approach to multiplication. This understanding of place value extends to multiplying numbers with more digits, building a solid foundation for more advanced arithmetic.
Beyond Arithmetic: Connections to Other Mathematical Fields
The simple equation of 30 x 10 extends far beyond basic arithmetic. Its principles underpin many advanced mathematical concepts:
-
Algebra: The equation can be represented algebraically as x * y = z, where x = 30, y = 10, and z = 300. This simple equation provides a foundational understanding for algebraic manipulation and equation solving.
-
Calculus: In calculus, multiplication is a fundamental operation used in differentiation and integration, concepts that form the basis of many advanced mathematical models and applications in science and engineering.
-
Linear Algebra: Matrix multiplication, a cornerstone of linear algebra, builds upon the fundamental principles of multiplication. Understanding 30 x 10 helps in understanding the fundamental concepts that underlie this advanced mathematical field.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 30 x 10?
A: The easiest way is to recognize that multiplying by 10 simply adds a zero to the end of the number. Therefore, 30 x 10 = 300.
Q: What are some real-world examples where 30 x 10 is used?
A: Real-world examples include calculating the total cost of multiple items, determining distances traveled, calculating the total number of objects in multiple containers, and scaling recipes.
Q: How can I use the concept of 30 x 10 to understand more complex multiplication problems?
A: Understanding 30 x 10 provides a basis for understanding the distributive property and place value, enabling you to break down larger multiplication problems into smaller, more manageable parts.
Q: Is there a connection between 30 x 10 and geometry?
A: Yes, 30 x 10 can be visualized as the area of a rectangle with length 30 units and width 10 units. This connection helps visualize and understand the multiplication concept more effectively.
Conclusion: The Enduring Significance of 30 x 10
The seemingly simple calculation of 30 x 10 serves as a gateway to a deeper understanding of mathematics. From the fundamental principles of multiplication to its visual representation through area and its applications in diverse fields, this equation highlights the power of basic arithmetic. Mastering this fundamental concept lays a solid foundation for tackling more complex mathematical problems and opens up a world of possibilities in various academic and professional endeavors. By understanding its underlying principles and applications, you unlock not only a mathematical skill but also a valuable tool for navigating the complexities of the real world. The journey from understanding 30 x 10 to grasping more advanced mathematical concepts is a testament to the power of building a strong foundation in basic arithmetic.
Latest Posts
Latest Posts
-
14 30 Simplified
Sep 13, 2025
-
1050mm In Cm
Sep 13, 2025
-
72 Miles Km
Sep 13, 2025
-
35pounds In Kg
Sep 13, 2025
-
10 Of 80000
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 30 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.