9/2 As Decimal
stanleys
Sep 14, 2025 · 6 min read
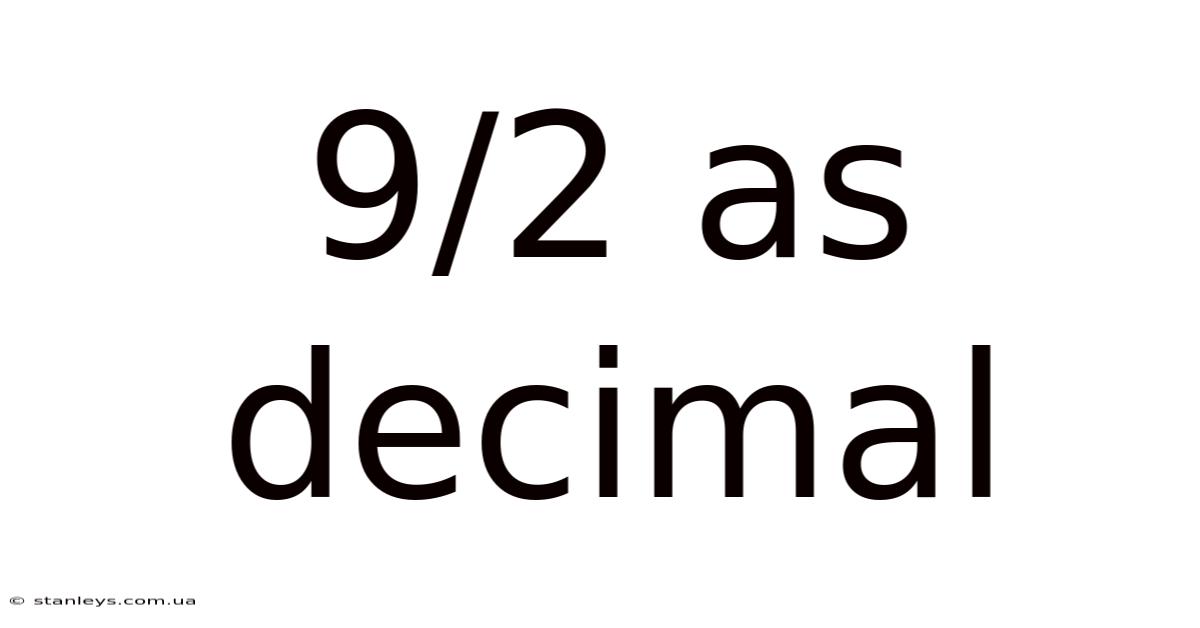
Table of Contents
9/2 as a Decimal: A Comprehensive Guide to Fraction to Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the fraction 9/2 into its decimal equivalent, explaining the process in detail and covering related concepts. We'll delve into various methods, discuss the significance of this specific conversion, and address frequently asked questions to solidify your understanding. By the end, you'll not only know the decimal value of 9/2 but also possess a strong foundation in fraction-to-decimal conversions.
Introduction: Understanding Fractions and Decimals
Before diving into the conversion of 9/2, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal represents a part of a whole using the base-ten number system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
The process of converting a fraction to a decimal involves dividing the numerator by the denominator. This seemingly simple process underlies a wealth of mathematical concepts and applications.
Method 1: Direct Division
The most straightforward method for converting 9/2 to a decimal is through direct division. We simply divide the numerator (9) by the denominator (2):
9 ÷ 2 = 4.5
Therefore, 9/2 as a decimal is 4.5.
Method 2: Equivalent Fractions
Another approach involves converting the fraction into an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000). While this method isn't always practical, it's useful for understanding the underlying principles. In this case, we can't directly convert 2 into a power of 10 using simple multiplication. However, this method highlights the connection between fractions and decimals more conceptually. For fractions with denominators that are factors of powers of 10 (like 2, 4, 5, 8, 10, etc.), this method is often easier.
Method 3: Understanding the Relationship Between Fractions and Decimals
To further grasp the concept, let's break down the fraction 9/2. It represents nine halves. One half (1/2) is equivalent to 0.5. Therefore, nine halves (9/2) is equivalent to 9 * 0.5 = 4.5. This method emphasizes the conceptual understanding of the fraction and its relationship to the decimal system. This is particularly helpful for visualizing the fraction's value.
The Significance of 9/2 and its Decimal Equivalent
The specific fraction 9/2, and its decimal equivalent 4.5, appears frequently in various mathematical contexts. For example:
- Geometry: When calculating areas or volumes of shapes, you might encounter 9/2 representing half of 9 units.
- Measurement: In engineering or construction, dimensions might be expressed in fractions, necessitating conversion to decimals for accurate calculations.
- Statistics: When calculating averages or means, you might encounter fractions that need converting to decimals for easier interpretation and comparison.
- Finance: In financial calculations involving percentages or ratios, converting fractions to decimals is essential for precision.
Extending the Concept: Converting Other Fractions to Decimals
The process of converting 9/2 to a decimal can be generalized to other fractions. The key is always to divide the numerator by the denominator. Let's consider a few examples:
- 1/4: 1 ÷ 4 = 0.25
- 3/8: 3 ÷ 8 = 0.375
- 5/6: 5 ÷ 6 = 0.8333... (this is a recurring decimal)
- 7/10: 7 ÷ 10 = 0.7
Note that some fractions result in terminating decimals (like 1/4 and 3/8), while others result in recurring decimals (like 5/6), which have a repeating pattern of digits.
Recurring Decimals and their Representation
Recurring decimals, also known as repeating decimals, are decimals with a pattern of digits that repeats infinitely. These are often represented with a bar over the repeating sequence. For example, 5/6 is represented as 0.8333... or 0.8$\overline{3}$. Understanding recurring decimals is crucial for working with fractions that don't have denominators that are powers of 2 or 5.
Decimal Places and Precision
The number of decimal places used depends on the required level of precision. In some applications, a few decimal places might suffice, while others require higher precision. For example, in engineering, high precision might be needed for accurate measurements. In everyday calculations, one or two decimal places are often sufficient.
Scientific Notation and Decimal Representation
For extremely large or small numbers, scientific notation is often used. This involves representing the number as a product of a number between 1 and 10 and a power of 10. Even with very large or small numbers expressed in scientific notation, the decimal portion of the number is still important for accuracy and interpretation.
Practical Applications of Fraction to Decimal Conversion
The ability to convert fractions to decimals is crucial in various real-world scenarios:
- Baking and Cooking: Recipes often use fractions for ingredient measurements. Converting these fractions to decimals can be helpful for using measuring tools that work with decimal values.
- Construction and Engineering: Precise measurements are critical in construction and engineering projects, so converting fractions to decimals ensures accuracy in calculations and measurements.
- Financial Calculations: Interest rates, discounts, and other financial calculations often involve fractions that need conversion to decimals for calculations and analysis.
- Data Analysis: Data analysis often involves manipulating numerical data, and converting fractions to decimals ensures uniformity and compatibility for calculations and interpretation.
Frequently Asked Questions (FAQ)
Q1: How can I convert a mixed number (e.g., 2 1/2) to a decimal?
A1: First, convert the mixed number to an improper fraction. In this example, 2 1/2 becomes 5/2. Then, divide the numerator (5) by the denominator (2): 5 ÷ 2 = 2.5.
Q2: What if the denominator of the fraction has prime factors other than 2 and 5?
A2: If the denominator contains prime factors other than 2 and 5, the resulting decimal will be a recurring decimal (repeating decimal).
Q3: Are there any online tools or calculators that can help with fraction to decimal conversions?
A3: Yes, many online calculators are available to assist with fraction-to-decimal conversions. Simply search for "fraction to decimal calculator" on the internet.
Q4: Why is it important to understand both fractions and decimals?
A4: Understanding both fractions and decimals provides a more comprehensive understanding of numbers and their relationships. Different situations lend themselves to using either fractions or decimals more effectively.
Q5: How do I handle very large fractions during conversion?
A5: For very large fractions, using a calculator or computer software is recommended to ensure accuracy. You can also break down very large fractions into smaller, more manageable components to ease the conversion process.
Conclusion: Mastering Fraction to Decimal Conversions
Converting fractions to decimals is a core skill in mathematics with broad applications across various fields. We've explored the conversion of 9/2 to its decimal equivalent (4.5) using different methods, highlighting the significance of this specific conversion and illustrating how the process can be extended to other fractions. By understanding the underlying principles and practicing different techniques, you can confidently convert fractions to decimals, enhancing your mathematical skills and problem-solving abilities. Remember, practice is key to mastering this fundamental mathematical skill. Continue practicing with different fractions to build your proficiency and confidence.
Latest Posts
Latest Posts
-
Pink To Yellow
Sep 14, 2025
-
Disadvantages Of Ssd
Sep 14, 2025
-
49 4kg In Stone
Sep 14, 2025
-
107cm In Ft
Sep 14, 2025
-
70 Of 400
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 9/2 As Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.