85 Of 20
stanleys
Sep 13, 2025 · 5 min read
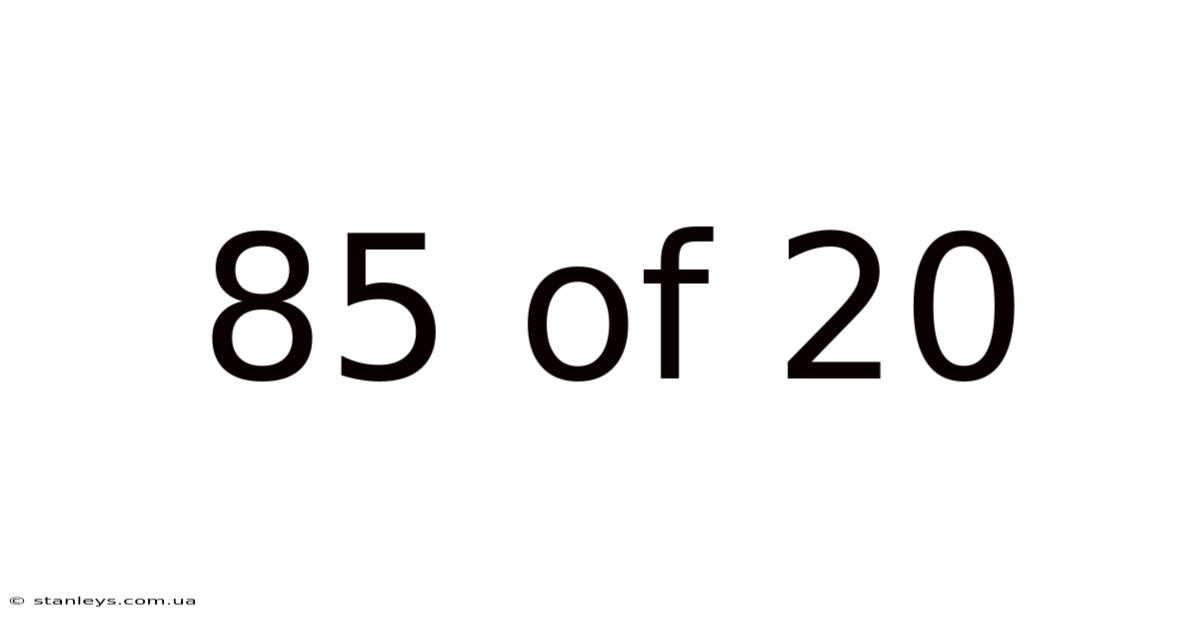
Table of Contents
Decoding 85% of 20: A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific calculations. This article delves into the meaning of "85% of 20," explaining not only the calculation itself but also the broader context of percentage calculations, their practical applications, and how to approach similar problems. This comprehensive guide will equip you with the knowledge to confidently tackle percentage-based questions in various scenarios.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of a hundred." Therefore, 85% literally means 85 out of 100, or 85/100. This fraction can be simplified to 17/20. This fundamental understanding is crucial for all percentage calculations.
Calculating 85% of 20: Step-by-Step
To find 85% of 20, we can use two primary methods:
Method 1: Converting Percentage to Decimal
-
Convert the percentage to a decimal: Divide the percentage by 100. In this case, 85% becomes 85 ÷ 100 = 0.85.
-
Multiply the decimal by the number: Multiply the decimal (0.85) by the number you want to find the percentage of (20). This gives us 0.85 x 20 = 17.
Therefore, 85% of 20 is 17.
Method 2: Using Fractions
-
Convert the percentage to a fraction: As mentioned earlier, 85% is equivalent to 85/100.
-
Multiply the fraction by the number: Multiply the fraction (85/100) by the number (20): (85/100) x 20 = 1700/100.
-
Simplify the fraction: Simplify the resulting fraction by dividing the numerator (1700) by the denominator (100): 1700/100 = 17.
Again, we arrive at the answer: 85% of 20 is 17.
Practical Applications of Percentage Calculations
The ability to calculate percentages is vital in many real-world situations. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations. For instance, understanding how much you'll save with a 25% discount on a $100 item directly relates to the core concepts discussed here.
-
Science and Statistics: Percentages are fundamental in expressing probabilities, statistical data, and experimental results. In scientific research, data is often presented as percentages to easily compare different results or groups. Think about surveys where responses are often summarized as percentages of the total.
-
Everyday Life: From calculating tips in restaurants to understanding sale prices in stores, percentages are integral to our daily lives. Figuring out the percentage of tasks completed in a project, or calculating your grade in a class based on weighted percentages, are common examples.
-
Business and Economics: Companies use percentages to analyze market share, growth rates, and profitability. Economic indicators such as inflation and unemployment rates are expressed as percentages. Understanding these percentages is critical for making informed business decisions.
-
Health and Fitness: Tracking progress in fitness, such as calculating body fat percentage or progress towards a fitness goal, often uses percentage calculations. Similarly, health statistics related to disease prevalence are often presented as percentages.
Expanding on Percentage Calculations: More Complex Scenarios
While the calculation of 85% of 20 is relatively straightforward, let's explore more complex scenarios to build your understanding:
-
Finding the Percentage: Instead of finding the percentage of a number, you might need to find what percentage one number is of another. For example, what percentage is 17 of 20? This involves dividing 17 by 20 and multiplying by 100, resulting in 85%.
-
Finding the Original Number: You might know the percentage and the resulting value, and need to find the original number. For example, if 85% of a number is 17, what is the original number? This requires setting up an equation: 0.85x = 17. Solving for x gives you the original number (20).
-
Multiple Percentages: Sometimes, you need to apply multiple percentages sequentially. For example, you might have a 10% discount followed by a 5% sales tax. You must calculate each percentage step-by-step, considering the intermediate results.
Addressing Common Misconceptions
Several common mistakes occur when working with percentages:
-
Confusing percentage change with absolute change: A 10% increase on 100 is 10, but a 10% increase on 1000 is 100. The percentage change is the same, but the absolute change is vastly different.
-
Incorrectly applying multiple percentages: Simply adding or subtracting percentages directly is often wrong, especially when applied sequentially. Always calculate each percentage based on the current value.
-
Not considering the base value: The base value (the number you're finding the percentage of) is crucial. Always clearly identify this value before starting any calculations.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages? The easiest way depends on your comfort level. Converting the percentage to a decimal and multiplying is often the quickest method for most people.
Q: Are there online calculators for percentages? Yes, many online calculators are available to help with percentage calculations. However, understanding the underlying principles is crucial for more complex scenarios.
Q: How can I improve my understanding of percentages? Practice is key. Try working through various examples, including different types of problems, such as finding percentages, finding the original number, or working with multiple percentages.
Conclusion
Understanding percentages is a crucial skill with broad applicability. While the calculation of 85% of 20 might seem simple, mastering this concept opens the door to tackling more complex percentage problems in finance, science, everyday life, and many other fields. By understanding the underlying principles and practicing different calculation methods, you can confidently apply percentage calculations in various situations. Remember to break down complex problems into smaller, manageable steps, and always double-check your work to minimize errors. With consistent practice and a solid grasp of the fundamental concepts, you'll develop a strong and reliable skillset in working with percentages.
Latest Posts
Latest Posts
-
80 4kg In Stone
Sep 13, 2025
-
64 Times Table
Sep 13, 2025
-
6 7 8
Sep 13, 2025
-
1 5 Of 20
Sep 13, 2025
-
70 Of 600
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.