1/5 Of 20
stanleys
Sep 13, 2025 · 5 min read
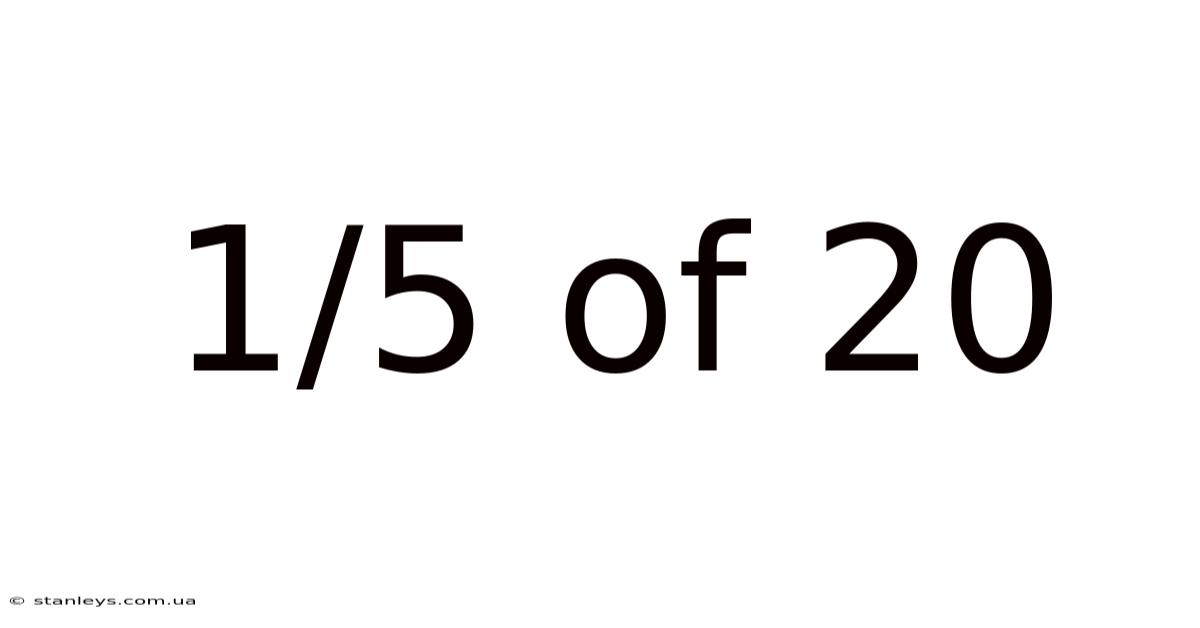
Table of Contents
Unpacking 1/5 of 20: A Deep Dive into Fractions, Decimals, and Percentages
This article explores the seemingly simple calculation of "1/5 of 20," delving beyond the immediate answer to understand the underlying mathematical concepts and their practical applications. We'll cover fractions, decimals, percentages, and explore how these concepts interconnect, providing a solid foundation for anyone looking to improve their numerical literacy. This comprehensive guide is perfect for students, educators, and anyone interested in strengthening their math skills.
Introduction: Understanding the Fundamentals
The expression "1/5 of 20" represents a fundamental mathematical operation involving fractions. It asks us to find one-fifth of the total quantity 20. While the calculation itself is relatively straightforward, understanding the principles behind it opens doors to more complex mathematical problems and real-world applications. This article will break down the process step-by-step, explaining the logic and providing alternative methods to arrive at the solution. We will also discuss the connections between fractions, decimals, and percentages, demonstrating their interchangeability and practical uses.
Method 1: Direct Fraction Multiplication
The most direct way to solve "1/5 of 20" is to treat "of" as multiplication. In mathematics, "of" often signifies multiplication. Therefore, the problem translates to:
(1/5) * 20
To multiply a fraction by a whole number, we can multiply the numerator (the top number) by the whole number and keep the denominator (the bottom number) the same:
(1 * 20) / 5 = 20/5
Finally, we simplify the fraction by dividing the numerator by the denominator:
20/5 = 4
Therefore, 1/5 of 20 is 4.
Method 2: Simplifying Before Multiplication
We can also simplify the calculation before performing the multiplication. Notice that 20 is divisible by 5:
20/5 = 4
This simplifies our problem to:
1/1 * 4 = 4
This method demonstrates the power of simplification in making calculations more efficient. It highlights that understanding the properties of numbers can significantly reduce the complexity of mathematical operations.
Method 3: Using Decimals
Fractions and decimals are interchangeable representations of the same value. The fraction 1/5 can be converted to a decimal by dividing the numerator by the denominator:
1 ÷ 5 = 0.2
Now, we can multiply the decimal by 20:
0.2 * 20 = 4
This approach reinforces the equivalence between fractions and decimals, demonstrating that the same result can be achieved using different numerical representations.
Method 4: Applying Percentages
Percentages offer another way to approach the problem. The fraction 1/5 is equivalent to 20%. To find 20% of 20, we can use the following formula:
(Percentage/100) * Total Value = Result
(20/100) * 20 = 4
This method highlights the interconnectedness of fractions, decimals, and percentages, showcasing their flexibility in solving mathematical problems. Converting 1/5 to a percentage (20%) allows us to utilize a common percentage calculation method, furthering our understanding of proportional relationships.
Expanding the Understanding: Fractions, Decimals, and Percentages
The calculation of "1/5 of 20" provides a springboard to explore the relationships between fractions, decimals, and percentages in greater depth. These three representations are fundamental to understanding various mathematical concepts and their applications in everyday life.
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts, while the numerator indicates the number of parts being considered.
-
Decimals: Decimals are another way of representing fractions. They use a base-ten system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.2 is equivalent to 2/10, which simplifies to 1/5.
-
Percentages: Percentages express fractions or decimals as parts of a hundred. They are often used to represent proportions or rates. For instance, 20% is equivalent to 20/100, which simplifies to 1/5.
Practical Applications
Understanding fractions, decimals, and percentages is crucial for numerous real-world applications. These include:
-
Financial Calculations: Calculating discounts, interest rates, taxes, and tips all involve fractions, decimals, and percentages.
-
Cooking and Baking: Recipes often use fractions to specify ingredient quantities.
-
Construction and Engineering: Precise measurements and calculations are essential in construction and engineering, often requiring the use of fractions and decimals.
-
Data Analysis: Interpreting data often involves calculating percentages and proportions.
-
Everyday Budgeting: Managing personal finances effectively requires understanding and utilizing fractions, decimals, and percentages.
Frequently Asked Questions (FAQ)
- What is the simplest form of the fraction 1/5?
The fraction 1/5 is already in its simplest form because the numerator (1) and the denominator (5) have no common factors other than 1.
- How do I convert a fraction to a decimal?
Divide the numerator by the denominator. For example, to convert 1/5 to a decimal, divide 1 by 5, resulting in 0.2.
- How do I convert a decimal to a percentage?
Multiply the decimal by 100 and add a percent sign (%). For example, to convert 0.2 to a percentage, multiply 0.2 by 100, resulting in 20%.
- How do I convert a percentage to a fraction?
Write the percentage as a fraction with a denominator of 100, then simplify the fraction. For example, to convert 20% to a fraction, write it as 20/100, which simplifies to 1/5.
Conclusion: Beyond the Calculation
While the answer to "1/5 of 20" is simply 4, the journey to arrive at that answer provides a valuable opportunity to reinforce fundamental mathematical concepts. Understanding the interconnectedness of fractions, decimals, and percentages, along with their practical applications, is key to developing a strong foundation in mathematics and numerical literacy. This knowledge empowers individuals to approach more complex problems with confidence and efficiency, and to apply these skills effectively in various aspects of life. Remember, mastering the basics opens doors to a deeper understanding of the mathematical world. The seemingly simple calculation of "1/5 of 20" serves as a powerful example of this principle.
Latest Posts
Latest Posts
-
Microlitres To Ml
Sep 13, 2025
-
66 Inches Feet
Sep 13, 2025
-
Pints Into Grams
Sep 13, 2025
-
10 Of 18
Sep 13, 2025
-
78 8kg To Stone
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1/5 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.