77 X 2
stanleys
Sep 17, 2025 · 5 min read
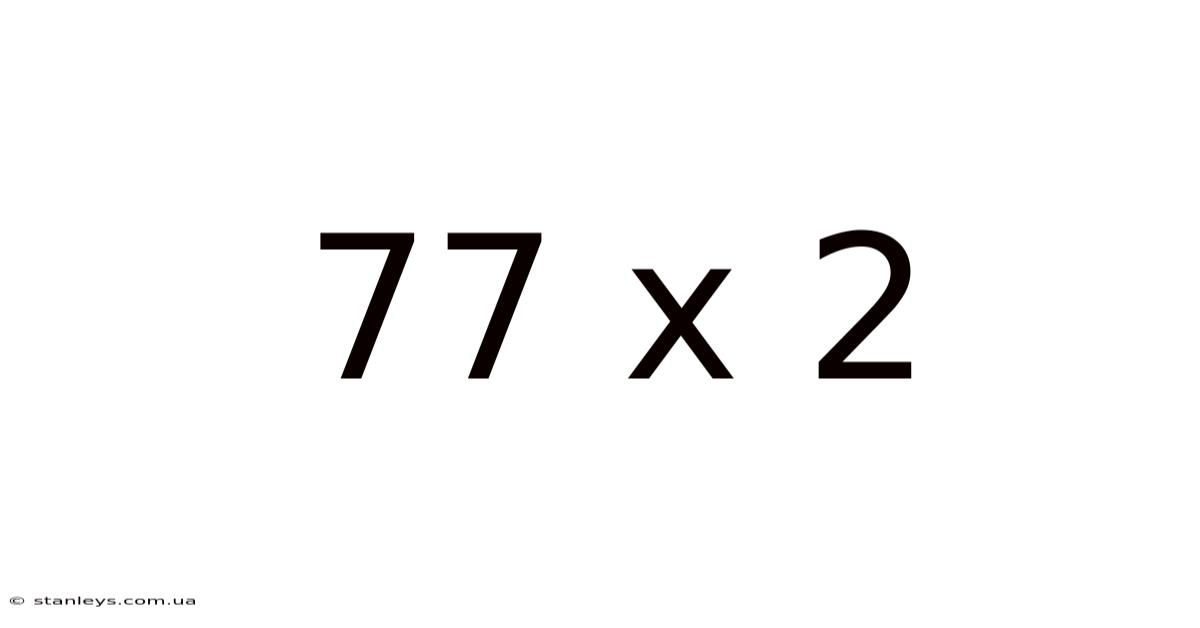
Table of Contents
Unpacking the Seemingly Simple: A Deep Dive into 77 x 2
This article explores the seemingly simple mathematical equation, 77 x 2, delving far beyond the immediate answer. We'll unpack the fundamental concepts involved, explore different approaches to solving the problem, examine its applications in real-world scenarios, and even touch upon its relevance in higher-level mathematics. This deep dive is perfect for anyone seeking a more profound understanding of basic arithmetic, its underlying principles, and its surprising connections to broader mathematical concepts.
Introduction: More Than Just an Answer
At first glance, 77 x 2 seems trivial. A quick calculation reveals the answer: 154. However, this seemingly straightforward equation offers a rich opportunity to explore fundamental mathematical concepts and problem-solving strategies. This exploration goes beyond simply finding the product; it's about understanding why the multiplication works, how it can be approached in various ways, and its wider implications in mathematics and everyday life.
Methods for Solving 77 x 2: A Multifaceted Approach
While the answer is easily obtained using a calculator or mental math, let's explore different methods to solve 77 x 2, highlighting various mathematical principles:
-
Standard Multiplication: The most common approach involves the standard multiplication algorithm learned in elementary school. We multiply 77 by 2, starting with the ones place: 2 x 7 = 14. We write down '4' and carry-over '1'. Then, we multiply 2 x 7 (in the tens place) and add the carry-over: 2 x 7 + 1 = 15. Therefore, 77 x 2 = 154. This method emphasizes place value and the distributive property.
-
Distributive Property: The distributive property states that a(b + c) = ab + ac. We can apply this to solve 77 x 2:
77 x 2 = (70 + 7) x 2 = (70 x 2) + (7 x 2) = 140 + 14 = 154. This method breaks down the problem into simpler multiplications, making it easier to solve mentally.
-
Doubling: Since multiplying by 2 is the same as doubling, we can simply double 77. This can be done mentally by doubling the tens place (70 becomes 140) and then doubling the ones place (7 becomes 14), and adding the results: 140 + 14 = 154. This method leverages intuitive understanding of doubling.
-
Repeated Addition: Although less efficient for larger numbers, we can solve this equation by repeatedly adding 77: 77 + 77 = 154. This method underscores the relationship between multiplication and addition.
Real-World Applications: 77 x 2 in Action
While seemingly abstract, the concept of 77 x 2 and the underlying principles of multiplication have widespread real-world applications:
-
Shopping: Imagine buying two items that cost $77 each. The total cost would be 77 x 2 = $154.
-
Measurement: If you need to measure two lengths, each measuring 77 centimeters, the total length would be 154 centimeters.
-
Inventory Management: A warehouse has two pallets of goods, each containing 77 items. The total number of items is 154.
-
Recipe Scaling: A recipe calls for 77 grams of flour, and you want to double the recipe. You'll need 154 grams of flour. These simple everyday examples demonstrate how fundamental multiplication is to various aspects of our lives.
Exploring the Number 154: A Deeper Dive
The result of 77 x 2, 154, itself holds some mathematical interest:
-
Factors: The factors of 154 are 1, 2, 7, 11, 14, 22, 77, and 154. Analyzing factors helps understand the number's divisibility and relationships to other numbers.
-
Prime Factorization: The prime factorization of 154 is 2 x 7 x 11. This representation shows the fundamental building blocks of the number.
-
Divisibility Rules: 154 is divisible by 2 (even number), 7 (sum of digits 1+5+4=10, not divisible by 7 directly but the number itself is), and 11 (difference between the alternating sum of digits is 1-5+4 = 0, divisible by 11).
Connecting to Higher-Level Mathematics
While seemingly basic, 77 x 2 connects to more complex mathematical concepts:
-
Algebra: This equation can be expressed algebraically as 2x = 154, where x represents 77. Solving for x involves algebraic manipulation.
-
Number Theory: The exploration of factors and prime factorization leads into number theory, a branch of mathematics dealing with properties of numbers.
-
Modular Arithmetic: In modular arithmetic, we consider remainders after division. For example, 154 modulo 10 is 4 (the remainder when 154 is divided by 10). This concept has applications in cryptography and computer science.
-
Abstract Algebra: The concept of multiplication itself is a fundamental operation explored in abstract algebra, where it's studied in the context of groups, rings, and fields. Understanding 77 x 2 helps build a foundation for grasping these more advanced algebraic structures.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 77 x 2?
A: Doubling is often the quickest method for multiplying by 2. Simply double 70 (140) and double 7 (14), then add the results (140 + 14 = 154).
Q: Why is the distributive property important in this calculation?
A: The distributive property allows us to break down a complex multiplication problem into simpler ones, making it easier to solve mentally or using pencil and paper.
Q: Are there any real-world examples beyond those mentioned?
A: Yes, countless situations involve multiplying by 2. Anything involving doubling quantities, costs, measurements, or scaling recipes uses this basic multiplication.
Q: What are some other ways to represent 77 x 2?
A: You could represent it as 77 + 77, or as (70 + 7) x 2, or even graphically as two sets of 77 objects.
Conclusion: The Significance of Simplicity
The seemingly simple equation 77 x 2 provides a gateway to understanding fundamental mathematical concepts, problem-solving strategies, and real-world applications. By exploring different methods of calculation, analyzing the resultant number (154), and connecting it to broader mathematical principles, we unveil a depth far exceeding initial expectations. This exercise highlights the significance of even the simplest mathematical operations and encourages a deeper appreciation for the beauty and power of mathematics. Remember, the key is not just getting the answer, but understanding the why behind it. This principle applies to all levels of mathematical understanding and problem-solving.
Latest Posts
Latest Posts
-
Social Context Meaning
Sep 17, 2025
-
Witty Remark Crossword
Sep 17, 2025
-
6 5inches In Cm
Sep 17, 2025
-
2x 10 Factored
Sep 17, 2025
-
179 X 2
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 77 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.