179 X 2
stanleys
Sep 17, 2025 · 6 min read
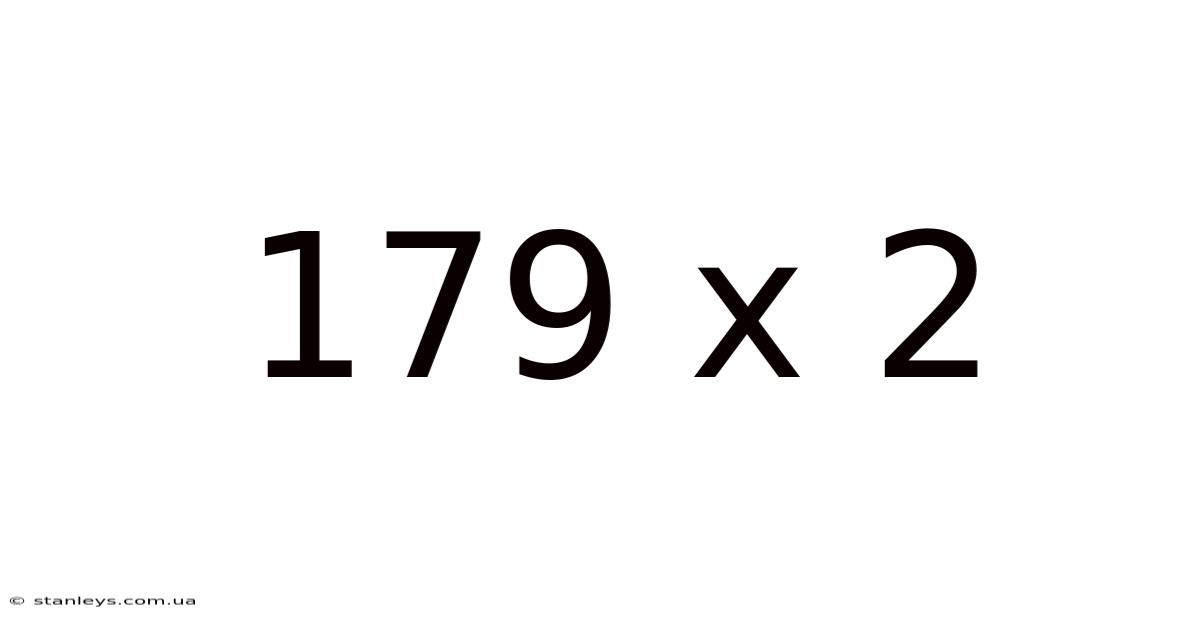
Table of Contents
Decoding 179 x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 179 x 2, delving far beyond the immediate answer to illuminate the underlying principles of multiplication, its various applications across different fields, and its significance in mathematics education. Understanding this basic operation is fundamental to grasping more complex mathematical concepts. We will explore different methods of solving this problem, examine its relevance in real-world scenarios, and even touch upon the historical context of multiplication. This comprehensive guide is designed for learners of all ages and backgrounds, aiming to build a strong foundation in arithmetic and problem-solving.
I. Introduction: The Fundamentals of Multiplication
Multiplication, at its core, is repeated addition. When we say 179 x 2, we are essentially asking: what is the sum of 179 added to itself? This simple interpretation helps to visualize the operation and grasp its meaning, especially for beginners. The number 179 is called the multiplicand, while 2 is the multiplier. The result, 358, is the product. Understanding these terms is crucial for building a strong mathematical vocabulary.
While 179 x 2 might seem trivial, it serves as a building block for understanding more complex multiplications, fractions, algebra, and even calculus. The concepts learned here extend far beyond this specific calculation.
II. Methods for Calculating 179 x 2
There are several ways to calculate 179 x 2, each offering different insights and catering to various learning styles:
-
Repeated Addition: This is the most basic approach. Add 179 to itself: 179 + 179 = 358. This method reinforces the fundamental definition of multiplication.
-
Standard Multiplication Algorithm: This involves multiplying each digit of the multiplicand (179) by the multiplier (2), starting from the rightmost digit (units place).
- 2 x 9 = 18 (write down 8, carry-over 1)
- 2 x 7 = 14 + 1 (carry-over) = 15 (write down 5, carry-over 1)
- 2 x 1 = 2 + 1 (carry-over) = 3 (write down 3)
- Result: 358
-
Distributive Property: This method breaks down the multiplication into smaller, more manageable parts. We can rewrite 179 as 100 + 70 + 9. Then, we apply the distributive property:
- 2 x (100 + 70 + 9) = (2 x 100) + (2 x 70) + (2 x 9) = 200 + 140 + 18 = 358. This method highlights the relationship between multiplication and addition.
-
Mental Math: With practice, one can perform this calculation mentally. This involves breaking down the number 179 into its hundreds, tens, and units, and multiplying each part separately before adding the results. For example, doubling 100 gives 200, doubling 70 gives 140, and doubling 9 gives 18. Adding 200 + 140 + 18 yields 358.
III. Real-World Applications of Multiplication
The seemingly simple calculation of 179 x 2 has countless real-world applications:
-
Shopping: Imagine buying two items that cost $179 each. The total cost is 179 x 2 = $358. This applies to any scenario involving purchasing multiple identical items.
-
Construction: If a builder needs 179 bricks for one section of a wall and needs to build two identical sections, they will need 179 x 2 = 358 bricks.
-
Cooking: A recipe calls for 179 grams of flour, and you want to double the recipe. You'll need 179 x 2 = 358 grams of flour.
-
Travel: If a car travels at an average speed of 179 kilometers per hour for two hours, the total distance covered would be 179 x 2 = 358 kilometers.
-
Finance: Calculating interest, income, or expenses often involves multiplication. For example, if you have two investments earning $179 each, your total earnings would be $358.
These examples highlight how fundamental multiplication is to our daily lives, extending beyond the classroom into various practical applications.
IV. Multiplication in Different Number Systems
While we've focused on the decimal system (base 10), multiplication operates across different number systems. For instance, in the binary system (base 2), 179 (which is 10110011 in binary) multiplied by 2 is simply a left bit-shift, resulting in 101100110 (which is 358 in decimal). This illustrates the underlying principles of multiplication remain consistent across different bases.
V. The Historical Context of Multiplication
Multiplication has a rich history, evolving over centuries. Ancient civilizations developed various methods for multiplication, including the use of counting boards, abacuses, and sophisticated algorithms. The development of the standard multiplication algorithm we use today is a testament to human ingenuity and the gradual refinement of mathematical techniques. The Egyptians used a method of doubling and adding, while the Babylonians used a sexagesimal system (base 60). Studying these historical methods provides valuable insights into the evolution of mathematics and the enduring relevance of fundamental operations like multiplication.
VI. Multiplication and its Relationship to Other Mathematical Concepts
Understanding 179 x 2 provides a gateway to understanding more complex mathematical concepts:
-
Algebra: Multiplication is fundamental to algebraic expressions and equations. It forms the basis for solving linear equations and other more complex algebraic problems.
-
Geometry: Calculating areas and volumes often involves multiplication. For example, the area of a rectangle is length multiplied by width.
-
Calculus: Differential and integral calculus rely heavily on the concept of limits, which are fundamentally connected to multiplication and division.
-
Statistics and Probability: Multiplication plays a vital role in calculating probabilities and analyzing statistical data.
VII. Addressing Common Misconceptions
A common misconception is that multiplication always results in a larger number. While it's generally true when multiplying by a number greater than 1, multiplying by a number less than 1 (e.g., fractions or decimals) will result in a smaller number. Understanding this nuance is crucial for mastering multiplication.
VIII. Practical Exercises and Further Exploration
To solidify your understanding of multiplication, consider solving the following problems:
- Calculate 235 x 2.
- Calculate 179 x 3.
- Explain how the distributive property can be used to calculate 346 x 2.
- Research and describe a historical method of multiplication used by a specific civilization.
- Explore the application of multiplication in a field that interests you (e.g., computer science, finance, physics).
IX. Conclusion: The Enduring Importance of Multiplication
The seemingly simple calculation of 179 x 2 serves as a powerful illustration of the fundamental principles of multiplication. Its applications are vast, extending far beyond simple arithmetic problems into various aspects of our daily lives and across multiple disciplines. Understanding this basic operation is not just about finding the answer (358); it's about grasping the underlying concepts, developing problem-solving skills, and building a strong foundation for more advanced mathematical concepts. The journey of learning mathematics begins with such foundational steps, and each step forward enhances our ability to understand and interact with the world around us. Continue exploring, practicing, and delving deeper into the fascinating world of mathematics!
Latest Posts
Latest Posts
-
10 Of 7
Sep 17, 2025
-
80lbs To Stone
Sep 17, 2025
-
50 To Fraction
Sep 17, 2025
-
123 Pounds Kg
Sep 17, 2025
-
6 Of 20000
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 179 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.