75 Of 500
stanleys
Sep 15, 2025 · 6 min read
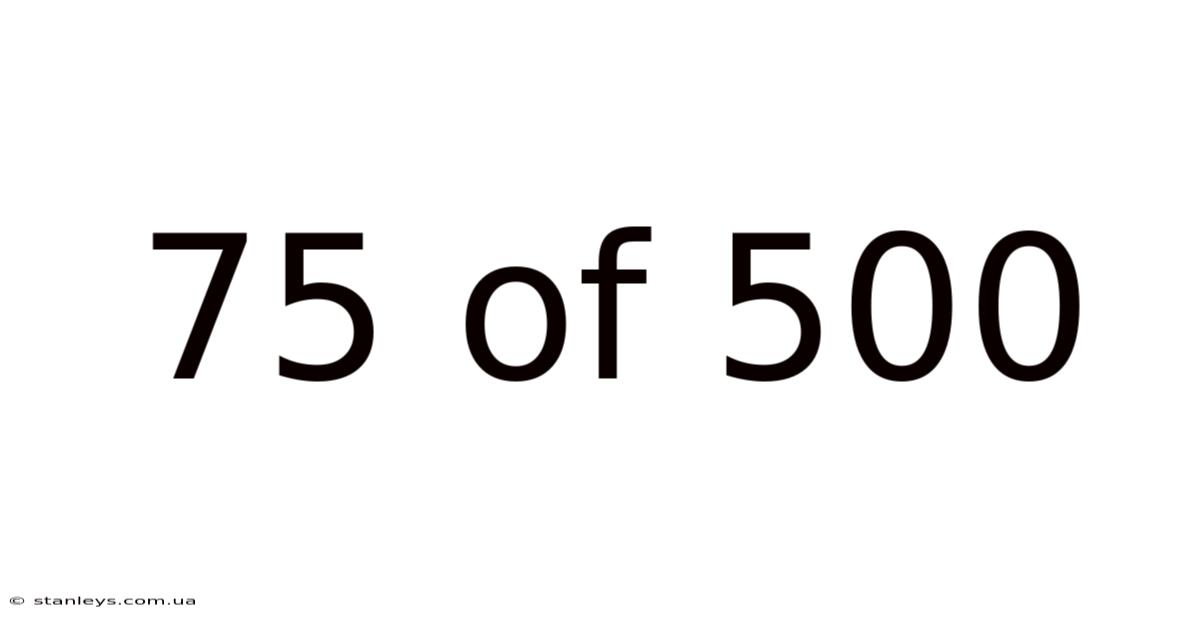
Table of Contents
Decoding the Fraction: Understanding 75/500 and its Implications
The seemingly simple fraction 75/500 might appear insignificant at first glance. However, understanding its implications extends far beyond basic arithmetic. This fraction represents a ratio, a proportion, and can be used to represent various real-world scenarios, from calculating percentages to analyzing data in scientific studies. This article will delve deep into understanding 75/500, exploring its simplification, percentage representation, applications, and the broader mathematical concepts it embodies.
I. Simplifying the Fraction: Finding the Lowest Terms
The first step in understanding 75/500 is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator (75) and the denominator (500) and dividing both by it.
Let's find the prime factorization of both numbers:
- 75 = 3 x 5 x 5 = 3 x 5²
- 500 = 2 x 2 x 5 x 5 x 5 = 2² x 5³
The common factors are 5 and 5 (or 5²). Therefore, the GCD is 25.
Dividing both the numerator and denominator by 25, we get:
75 ÷ 25 = 3 500 ÷ 25 = 20
Therefore, the simplified fraction is 3/20. This simplified form is crucial as it makes further calculations and interpretations easier.
II. Converting to Percentage: Expressing the Fraction as a Proportion
Converting the fraction 75/500 (or its simplified form 3/20) into a percentage provides a clearer understanding of its proportional value. To convert a fraction to a percentage, we multiply the fraction by 100%.
Using the simplified fraction:
(3/20) x 100% = 15%
Therefore, 75/500 represents 15%. This percentage representation is incredibly useful for visualizing the proportion and comparing it with other percentages. For example, if 75 out of 500 students passed an exam, this means 15% of the students passed.
III. Real-World Applications: Understanding Contextual Meaning
The fraction 75/500, or its equivalent 15%, finds applications in a wide range of fields:
-
Statistics and Probability: In statistical analyses, this fraction could represent the proportion of successful trials in an experiment, the percentage of a population with a specific characteristic, or the probability of a particular event occurring. Understanding the percentage allows researchers to draw conclusions and make predictions.
-
Finance and Business: In finance, this fraction might represent the percentage of a company's revenue that comes from a specific product line, the percentage of a loan that has been repaid, or the percentage of market share held by a particular business. These applications are vital for decision-making and strategic planning.
-
Education and Testing: As mentioned earlier, in educational settings, 75/500 could represent the pass rate on an exam, the percentage of students completing an assignment, or the proportion of students achieving a particular grade level. This data informs teaching strategies and curriculum development.
-
Science and Engineering: In scientific studies, this fraction could signify the percentage of a sample exhibiting a certain trait, the percentage error in an experiment, or the percentage efficiency of a process. Accurate understanding of such proportions is critical for scientific rigor and the validity of results.
-
Everyday Life: Beyond formal contexts, understanding percentages is crucial in daily life. Calculating discounts, tips, or understanding proportions in recipes all involve the same fundamental concepts. For example, a 15% discount on a $100 item would save you $15.
IV. Expanding the Concept: Working with Ratios and Proportions
The fraction 75/500 is fundamentally a ratio, expressing the relationship between two quantities. It shows that for every 500 units of the whole, there are 75 units of a specific part. This concept extends to other ratios and proportions. For instance, if we were to maintain the same ratio, we could find out how many units of the part would exist if the whole were 1000 units:
(75/500) = (x/1000)
Solving for x:
x = (75 x 1000) / 500 = 150
This demonstrates the ability to scale ratios and proportions to different sizes while maintaining the same proportional relationship.
V. Advanced Applications: Exploring Percentage Change and Growth
Building upon the understanding of percentages, we can apply this knowledge to calculate percentage change or growth. Imagine a scenario where the number of students increased from 500 to 575. The increase is 75 students. To calculate the percentage increase:
(Increase / Original Value) x 100% = ((75/500) x 100%) = 15%
The number of students increased by 15%. This type of calculation is essential in various fields, from tracking population growth to analyzing financial investments.
VI. Addressing Potential Misconceptions: Common Errors to Avoid
Working with fractions and percentages can sometimes lead to common misconceptions. Here are a few to avoid:
-
Ignoring Simplification: Failing to simplify fractions can make calculations more complex and increase the risk of errors. Always simplify fractions to their lowest terms before performing further operations.
-
Incorrect Conversion to Percentage: Ensure the correct multiplication by 100% when converting a fraction to a percentage. A common mistake is to mistakenly divide by 100.
-
Misinterpreting Percentages: Context is crucial. Understanding the basis for the percentage is vital. A 15% increase from a small base value is different from a 15% increase from a large base value.
-
Confusing Percentage Change with Absolute Change: Remember that percentage change shows the relative change, whereas the absolute change is the actual difference in values.
VII. Frequently Asked Questions (FAQ)
- Q: What is the decimal equivalent of 75/500?
A: The decimal equivalent of 75/500 (or 3/20) is 0.15. This is obtained by dividing the numerator by the denominator.
- Q: Can 75/500 be expressed as a mixed number?
A: No, 75/500 (or 3/20) is a proper fraction because the numerator is smaller than the denominator. Therefore, it cannot be expressed as a mixed number.
- Q: How can I apply this knowledge to solve real-world problems?
A: By understanding the concepts of ratios, proportions, and percentages, you can solve numerous real-world problems, from calculating discounts and sales tax to analyzing statistical data and making informed decisions in various fields.
VIII. Conclusion: The Significance of Understanding 75/500
The seemingly simple fraction 75/500, when thoroughly analyzed, reveals a wealth of mathematical concepts and practical applications. Understanding its simplification to 3/20, its percentage equivalent of 15%, and its relevance in different contexts empowers individuals to approach problems involving ratios, proportions, and percentages with confidence. This knowledge extends far beyond basic arithmetic, laying a strong foundation for more advanced mathematical studies and real-world problem-solving. Mastering these fundamental concepts provides a powerful tool for navigating various aspects of life, from personal finance to professional endeavors. Remember to always simplify, verify, and consider the context to accurately interpret and utilize these essential mathematical tools.
Latest Posts
Latest Posts
-
Until In French
Sep 16, 2025
-
65kg In St
Sep 16, 2025
-
122mm To Inches
Sep 16, 2025
-
Opposite Of Mercy
Sep 16, 2025
-
0 07 To Fraction
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.