65 Of 40
stanleys
Sep 12, 2025 · 5 min read
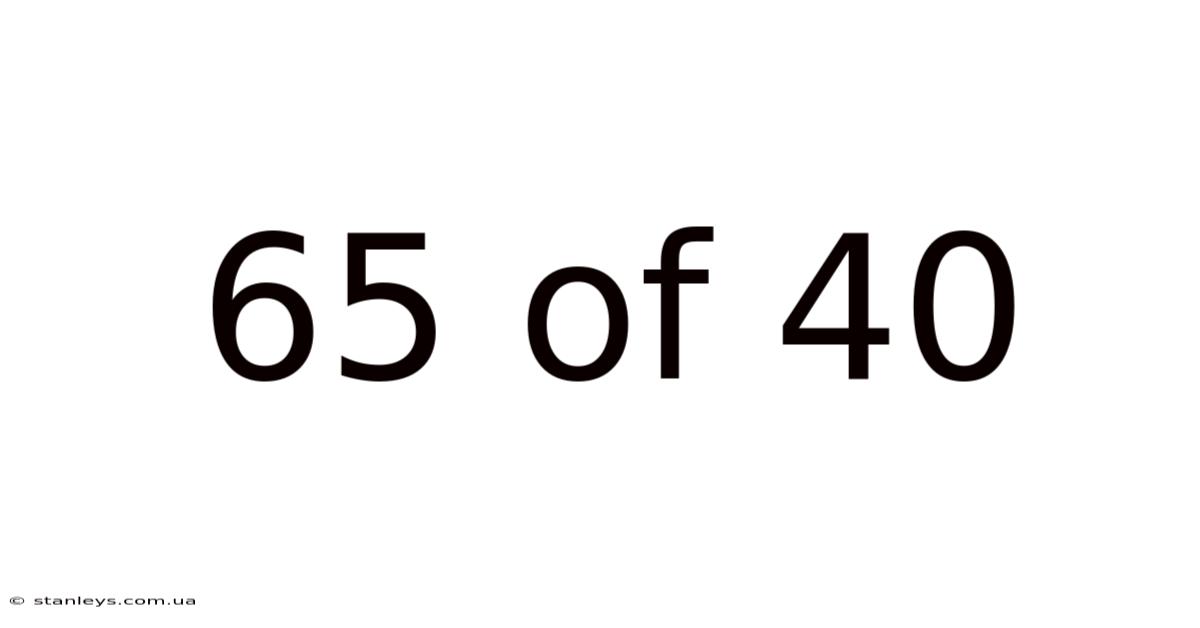
Table of Contents
Decoding the Mystery: Understanding "65 of 40" and its Implications
The phrase "65 of 40" might seem paradoxical at first glance. How can something be 65 out of 40? It appears to defy basic mathematical logic. This article delves into the possible interpretations of this unusual expression, exploring the scenarios where such a statement could be valid, and clarifying the underlying concepts to avoid future confusion. We'll examine different contexts, from simple misinterpretations to complex statistical analyses, ensuring a thorough understanding of this seemingly contradictory phrase. This exploration will cover various mathematical principles, highlighting the importance of context and precision in quantitative statements.
Possible Interpretations of "65 of 40"
The core problem with "65 of 40" lies in its ambiguity. The phrase lacks the necessary context to determine its intended meaning. Let's explore several plausible interpretations:
1. Simple Mathematical Error:
The most straightforward interpretation is a simple mistake. Perhaps the numbers were transposed, and the intended meaning was "40 of 65" representing a fraction or percentage. This highlights the importance of double-checking figures, especially in quantitative reports or analyses. Human error is a common source of such discrepancies. It emphasizes the need for careful data entry and verification processes to ensure accuracy.
2. Overlapping or Cumulative Data:
Imagine a scenario involving surveys or data collection. "65 of 40" could signify that 65 responses were received, even though the initial target or expected number was only 40. This surplus might indicate a highly successful survey, exceeding expectations. Alternatively, the 40 could represent a specific subset of the data, while the 65 encompasses a broader category. For instance, 40 might represent respondents from a specific demographic group, while the total number of respondents is 65.
3. Weighted Averages or Proportions:
In certain statistical contexts, "65 of 40" could represent weighted averages or proportions. Suppose a certain metric is calculated across several different weighted categories. The individual weightings might sum to a value less than the final overall measure. A complex calculation could yield a result of 65, even though the sum of individual component values is 40. This is more likely in advanced statistical models or in scenarios involving complex datasets.
4. Units of Measurement:
Consider the possibility that the numbers represent different units. Perhaps "65" refers to one type of measurement (e.g., centimeters, kilograms, or currency units), while "40" refers to a different type of measurement. Without knowing the units, the phrase remains meaningless. This points towards the critical importance of specifying units when dealing with numerical data to ensure clarity and avoid ambiguity.
5. Contextual Misinterpretation:
The meaning of "65 of 40" could be dependent entirely on the surrounding context. The surrounding text or situation could clarify the meaning. Without this essential context, any interpretation remains speculative. Always look at the larger picture when encountering seemingly contradictory data.
Exploring Related Mathematical Concepts
Understanding the implications of "65 of 40" requires exploring several related mathematical concepts:
Percentages and Fractions:
If we were to interpret "65 of 40" as a fraction, it would be 65/40, which simplifies to 13/8 or 1.625. Expressed as a percentage, this is 162.5%. This high percentage signifies that the numerator significantly exceeds the denominator, further emphasizing the unusual nature of the statement. However, this interpretation relies on the assumption that "of" signifies a fraction or ratio.
Ratios and Proportions:
Ratios compare two quantities. The ratio 65:40 simplifies to 13:8. This ratio indicates that for every 8 units of one quantity, there are 13 units of another. The context is crucial to interpret the meaning of this ratio. This interpretation provides a different perspective on the relationship between 65 and 40.
Statistical Measures:
In statistics, we often encounter values that seem counterintuitive at first. Weighted averages, standard deviations, and other statistical measures can produce results that don't align directly with simple sums or ratios. "65 of 40" might represent a summary statistic from a complex statistical analysis.
Data Aggregation and Analysis:
The phrase might arise from aggregating data from multiple sources. Various sources might contribute data, and the final aggregate value could be 65, even if individual sources had totals less than 40. This emphasizes the importance of understanding the data aggregation methodology when interpreting results.
Frequently Asked Questions (FAQ)
Q: Is "65 of 40" mathematically possible?
A: Mathematically, it's not possible in the straightforward sense of a simple fraction or ratio. However, within specific contexts like those discussed above (cumulative data, weighted averages, differing units), it can be interpreted meaningfully.
Q: What is the most likely explanation for "65 of 40"?
A: The most probable explanation is a data entry error or a misunderstanding of the data's underlying context. It's crucial to examine the source of the data and the surrounding information to determine the intended meaning.
Q: How can I avoid such ambiguous statements in my own work?
A: Always clearly define your units, variables, and methodology. Ensure proper data validation and verification to prevent errors. Use clear and unambiguous language when presenting quantitative data.
Conclusion: Context is King
The seemingly paradoxical phrase "65 of 40" underscores the importance of context in interpreting numerical data. Without sufficient information about the origin, method of calculation, and units involved, it's impossible to assign a definitive meaning. This situation highlights the critical role of precise communication and rigorous data handling in all quantitative fields. The lesson learned here is to always question ambiguous data, investigate its origin, and consider various possible interpretations before reaching any conclusions. Remember, a thorough understanding of the context is essential to make sense of even seemingly contradictory numbers. Always prioritize clarity and accuracy when dealing with numerical data to avoid such confusing scenarios and ensure a consistent and reliable interpretation. The ability to analyze and interpret data effectively depends heavily on careful consideration of every detail, especially the context surrounding the presented data.
Latest Posts
Latest Posts
-
61 4kg In Stone
Sep 12, 2025
-
1 9 8
Sep 12, 2025
-
Simplify 8 10
Sep 12, 2025
-
35 Of 10
Sep 12, 2025
-
Poem On Father
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 65 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.