60 Of 400
stanleys
Sep 12, 2025 · 5 min read
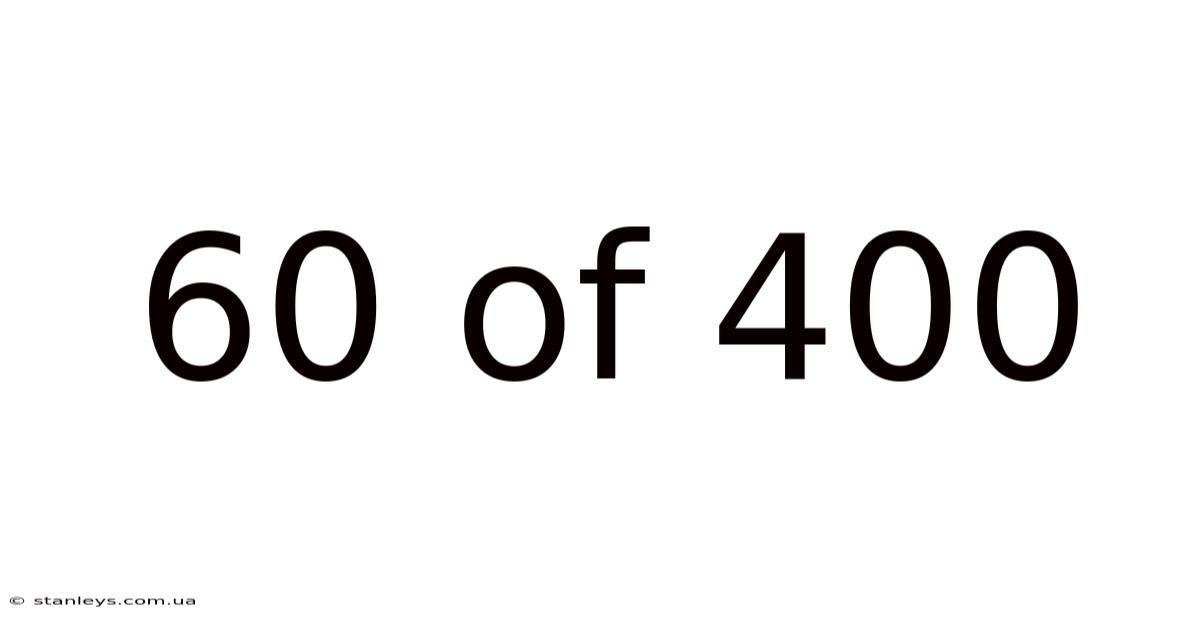
Table of Contents
Decoding the Mystery: Understanding 60 out of 400
Understanding fractions, percentages, and ratios is fundamental to many aspects of life, from calculating grocery bills to comprehending complex data in scientific research. This article delves into the meaning and implications of "60 out of 400," exploring its various representations, calculations, and real-world applications. We'll unpack this seemingly simple phrase, revealing its underlying mathematical principles and demonstrating its practical use in diverse contexts.
Introduction: What Does "60 out of 400" Mean?
The phrase "60 out of 400" represents a part-to-whole relationship. It signifies that 60 units are present within a total of 400 units. This can be applied to numerous scenarios, such as scoring on a test, analyzing survey results, or understanding production yields. The key to understanding this concept lies in recognizing it as a fraction, which can then be converted into a percentage or a decimal to facilitate comparison and analysis. This article will guide you through these conversions and highlight their practical significance.
Representing "60 out of 400" Mathematically
The simplest way to represent "60 out of 400" is as a fraction: 60/400. This fraction shows the ratio of the part (60) to the whole (400). We can then simplify this fraction by finding the greatest common divisor (GCD) of 60 and 400, which is 20. Dividing both the numerator and the denominator by 20, we get the simplified fraction 3/20. This simplification doesn't change the value; it merely represents the same ratio in its most concise form.
Key takeaway: Understanding the simplification process is crucial for accurate calculations and clear communication.
Converting to Percentage: Expressing the Ratio as a Percentage
Converting the fraction 60/400 (or its simplified form, 3/20) to a percentage is straightforward. We can perform the division: 60 divided by 400 equals 0.15. To express this as a percentage, we multiply by 100: 0.15 * 100 = 15%. Therefore, "60 out of 400" is equivalent to 15%.
Key takeaway: Percentages provide a standardized and easily understandable way to compare proportions. This conversion is essential for representing data in reports, presentations, and various other contexts.
Converting to Decimal: A Numerical Representation
The decimal equivalent of 60/400 is 0.15. This is obtained by simply performing the division: 60 ÷ 400 = 0.15. Decimals are useful for calculations, particularly when using computers or calculators. They provide a more precise numerical representation compared to percentages in some scenarios.
Key takeaway: Decimals are valuable for computational purposes and offer another way to represent proportions.
Real-World Applications: Understanding the Context
The significance of "60 out of 400" depends entirely on the context. Let's explore a few examples:
-
Test Scores: If 60 out of 400 points were achieved on a test, this represents a score of 15%. This score can then be compared to the scores of other students or to a predetermined passing grade.
-
Survey Results: If 60 out of 400 respondents answered "yes" to a particular question in a survey, this indicates that 15% of the respondents held that particular opinion. This percentage is crucial for understanding public opinion or preferences.
-
Production Yield: If a factory produces 60 usable items out of 400 attempts, this signifies a 15% yield rate. This low yield may indicate a problem in the production process and prompt investigation to improve efficiency.
-
Statistical Analysis: In statistical analyses, "60 out of 400" could represent a sample proportion. This sample proportion can be used to estimate the population proportion with a certain level of confidence, depending on the sample size and margin of error.
Expanding on the Concept: Proportionality and Ratios
The relationship between 60 and 400 illustrates the concept of proportionality. This means that the ratio between these two numbers remains constant even if the scale changes. For instance, if we were to double the quantities, we'd have 120 out of 800, which is still equivalent to 15%. Understanding proportionality is vital in various fields like scaling recipes, calculating map distances, or analyzing economic data. This forms the basis of many mathematical and scientific principles.
Advanced Concepts: Standard Deviation and Error
When dealing with larger datasets and statistical analysis, understanding concepts like standard deviation and margin of error becomes crucial. The 15% derived from "60 out of 400" is just a point estimate. To understand the precision of this estimate, we would need to consider the standard deviation of the sample and calculate confidence intervals to determine the range within which the true population proportion likely lies.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage from a fraction?
A: To calculate the percentage from a fraction like 60/400, divide the numerator (60) by the denominator (400), then multiply the result by 100.
Q: What is the simplified form of the fraction 60/400?
A: The simplified form is 3/20, obtained by dividing both the numerator and the denominator by their greatest common divisor, which is 20.
Q: Can I use a calculator to convert "60 out of 400" into a percentage?
A: Yes, simply divide 60 by 400 and then multiply by 100. Most calculators will automatically provide the percentage.
Q: What if I have a different number of items, for example, 75 out of 500? How would I solve that?
A: The same principles apply. Divide 75 by 500, then multiply by 100 to get the percentage. This will also simplify to 15%, illustrating the concept of proportionality.
Conclusion: The Power of Proportionality
Understanding the mathematical representation and implications of "60 out of 400" is more than just a simple calculation. It's a fundamental skill applicable to numerous areas of life. From everyday tasks to complex scientific and statistical analyses, the ability to convert fractions to percentages and decimals and to understand proportionality is crucial for clear communication, effective problem-solving, and informed decision-making. This seemingly simple phrase unlocks a world of mathematical concepts and practical applications, emphasizing the power of understanding ratios and proportions. Mastering this concept empowers you to navigate data-rich environments with greater confidence and efficiency.
Latest Posts
Latest Posts
-
1 9 Squared
Sep 12, 2025
-
140 In Kilograms
Sep 12, 2025
-
90lb In Stone
Sep 12, 2025
-
10 Of 600
Sep 12, 2025
-
Nm To Molar
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.