60 Of 250
stanleys
Sep 12, 2025 · 5 min read
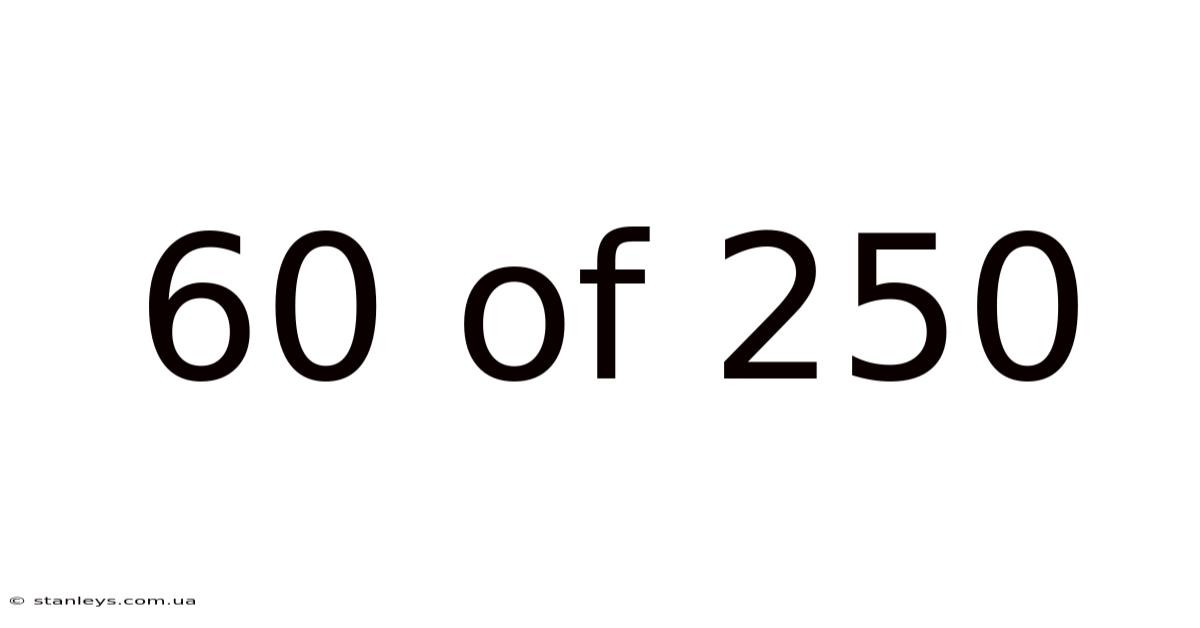
Table of Contents
Decoding the Fraction: Understanding 60/250 and its Implications
What does the fraction 60/250 truly represent? At first glance, it might seem like just another mathematical expression. However, understanding this fraction, and how to simplify and interpret it, opens doors to a deeper understanding of ratios, proportions, and their applications in various fields, from everyday life to complex scientific calculations. This article will delve into the intricacies of 60/250, providing a comprehensive guide to its simplification, its representation as a percentage and decimal, and its practical applications.
Simplifying 60/250: Finding the Greatest Common Divisor (GCD)
The first step in understanding 60/250 is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (60) and the denominator (250). The GCD is the largest number that divides both numbers without leaving a remainder.
One method to find the GCD is through prime factorization. Let's break down 60 and 250 into their prime factors:
- 60 = 2 x 2 x 3 x 5
- 250 = 2 x 5 x 5 x 5
By comparing the prime factorizations, we can identify the common factors: 2 and 5. The GCD is the product of these common factors: 2 x 5 = 10.
Now, we divide both the numerator and the denominator by the GCD:
- 60 ÷ 10 = 6
- 250 ÷ 10 = 25
Therefore, the simplified fraction is 6/25. This simplified form represents the same proportion as 60/250 but is more concise and easier to work with.
Another method to find the GCD is the Euclidean algorithm. This iterative method involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to 60 and 250:
- 250 = 4 x 60 + 10
- 60 = 6 x 10 + 0
The last non-zero remainder is 10, confirming that the GCD is indeed 10.
Representing 60/250 (or 6/25) as a Decimal and Percentage
Simplifying the fraction makes it easier to convert it into a decimal and a percentage. To convert a fraction to a decimal, simply divide the numerator by the denominator:
- 6 ÷ 25 = 0.24
Therefore, 60/250 is equivalent to 0.24 as a decimal.
To convert a decimal to a percentage, multiply by 100:
- 0.24 x 100 = 24%
So, 60/250 represents 24%. This percentage representation is often more intuitive and easily understood in many contexts.
Practical Applications of 60/250 (or 6/25)
The fraction 60/250, or its simplified form 6/25, has a wide range of practical applications depending on the context. Let's explore a few examples:
-
Performance Metrics: Imagine a student answering 60 out of 250 questions correctly on a test. Their score is 24%, reflecting their performance relative to the total number of questions. This percentage allows for easy comparison with other students or benchmarks.
-
Sales and Marketing: If a company sets a sales target of 250 units and sells 60 units, their sales performance is 24% of the target. This provides a clear picture of their progress towards the goal.
-
Survey Results: If 60 out of 250 respondents to a survey answered "yes" to a particular question, then 24% of respondents answered affirmatively. This allows for statistical analysis and interpretation of the survey data.
-
Probability: The fraction could represent the probability of a specific event occurring. For example, if there are 250 equally likely outcomes and 60 of them lead to a particular event, the probability of that event happening is 24%.
-
Recipe Scaling: If a recipe calls for 60 grams of ingredient A for 250 grams of the final product, you could scale the recipe down or up proportionally. For example, if you only need 100 grams of the final product, you'd need (100/250) * 60 = 24 grams of ingredient A.
Understanding Ratios and Proportions
The fraction 60/250 fundamentally represents a ratio. A ratio is a comparison of two quantities. In this case, it compares 60 to 250. This ratio can be expressed in different ways: 60:250, 6:25, or 0.24:1. All these representations convey the same proportional relationship.
A proportion is a statement that two ratios are equal. For example, the proportion 60/250 = 6/25 states that the ratio 60 to 250 is equal to the ratio 6 to 25. Understanding proportions is crucial for solving various problems involving scaling, percentages, and similar triangles.
Further Exploration: Beyond 60/250
While this article has focused on 60/250, the principles discussed apply to any fraction. Mastering the concepts of simplification, decimal and percentage conversions, and understanding ratios and proportions are fundamental skills in mathematics with applications extending far beyond simple fraction calculations. These skills are essential for success in various academic disciplines and professional fields.
Frequently Asked Questions (FAQ)
Q: Can I simplify 60/250 any further than 6/25?
A: No, 6/25 is the simplest form because the greatest common divisor of 6 and 25 is 1. They share no common factors other than 1.
Q: What if the numerator and denominator had more complex numbers? How would I find the GCD?
A: For larger numbers, prime factorization can become cumbersome. The Euclidean algorithm provides a more efficient method to find the GCD, regardless of the size of the numbers.
Q: Are there any online tools to help simplify fractions?
A: Yes, numerous online calculators and tools are available to simplify fractions. However, understanding the underlying principles of finding the GCD is crucial for a deeper understanding of mathematics.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and use in calculations. A simplified fraction represents the same proportion as the original fraction but in a more concise and manageable form. It also helps avoid unnecessary complexity in calculations.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple fraction 60/250 reveals a wealth of mathematical concepts and practical applications. By understanding how to simplify fractions, convert them to decimals and percentages, and grasp the underlying principles of ratios and proportions, you equip yourself with essential tools for tackling various challenges in numerous fields. This knowledge extends far beyond the classroom, empowering you to analyze data, solve problems, and make informed decisions in your personal and professional life. The journey of mastering fractions is not just about numbers; it's about developing crucial analytical and problem-solving skills that will serve you well throughout your life.
Latest Posts
Latest Posts
-
8x 12 Factored
Sep 12, 2025
-
1000 4
Sep 12, 2025
-
8 3kg To Lbs
Sep 12, 2025
-
Crispin Buxley Phenomenon
Sep 12, 2025
-
1200ml In Litres
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.