1000 / 4
stanleys
Sep 12, 2025 · 6 min read
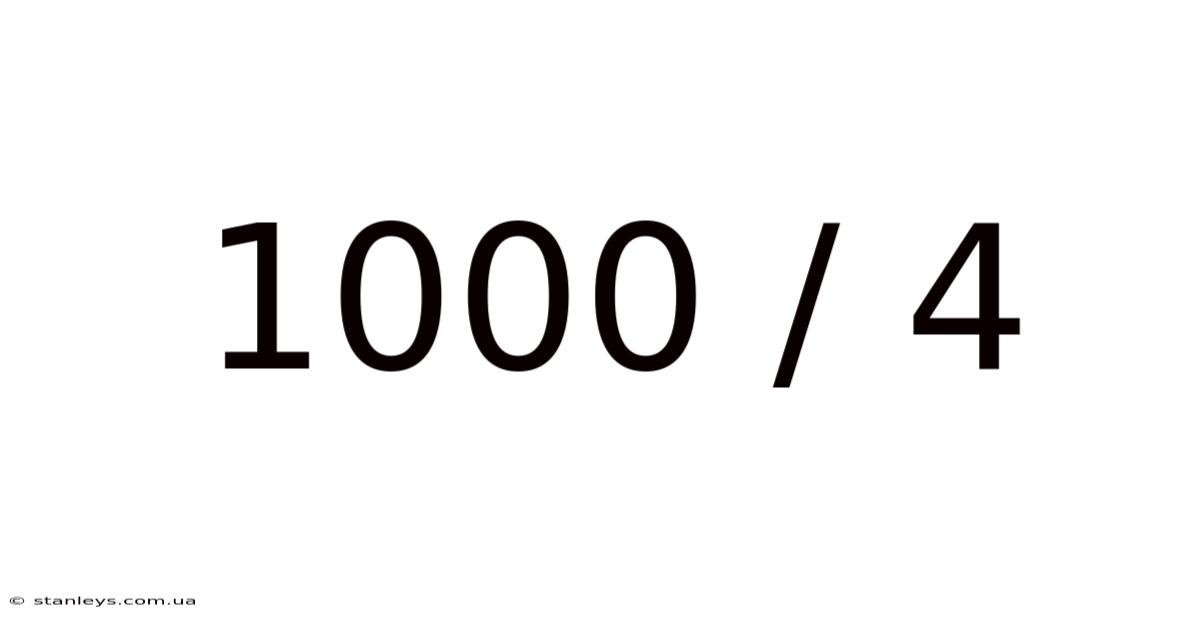
Table of Contents
Decoding 1000 / 4: A Deep Dive into Division and its Applications
This article explores the seemingly simple division problem, 1000 / 4, delving far beyond the immediate answer. We'll unpack the fundamental concepts of division, examine different methods for solving it, explore its real-world applications, and discuss the broader mathematical principles it embodies. Understanding 1000 / 4 is not just about getting the correct quotient; it's about grasping the underlying logic and its significance in various fields.
Introduction: What is Division?
Division, at its core, is the inverse operation of multiplication. While multiplication combines equal groups to find a total, division separates a total into equal groups or determines the size of each group. The equation 1000 / 4 asks: "If we have 1000 items and want to divide them equally into 4 groups, how many items will be in each group?" This simple question opens the door to a wealth of mathematical concepts. The number being divided (1000) is called the dividend, the number doing the dividing (4) is the divisor, and the result (250) is the quotient. Any remaining amount after the division is the remainder, although in this case, there is no remainder as 1000 is perfectly divisible by 4.
Methods for Solving 1000 / 4
Several methods can be used to solve 1000 / 4, each offering a different perspective on the problem:
- Long Division: This is a classic algorithm taught in schools. It involves systematically breaking down the dividend into smaller parts that are easily divisible by the divisor.
250
4 | 1000
-8
20
-20
00
-0
0
The process begins by dividing 4 into the first digit (1), which isn't possible. So, we consider the first two digits (10). 4 goes into 10 two times (2 x 4 = 8), leaving a remainder of 2. This remainder is carried over to the next digit (0), forming 20. 4 goes into 20 five times (5 x 4 = 20), leaving no remainder. Finally, we bring down the last 0, and 4 goes into 0 zero times. Thus, the quotient is 250.
-
Repeated Subtraction: This method involves repeatedly subtracting the divisor (4) from the dividend (1000) until the result is 0. The number of subtractions performed equals the quotient. While less efficient for large numbers, it visually demonstrates the concept of division as repeated subtraction.
-
Mental Math: With practice, one can solve 1000 / 4 mentally. Recognizing that 1000 is a multiple of 100, and 100 is easily divisible by 4 (100 / 4 = 25), we can deduce that 1000 / 4 = 250.
-
Fractions: The problem can be represented as a fraction: 1000/4. Simplifying this fraction involves finding the greatest common divisor (GCD) of 1000 and 4, which is 4. Dividing both the numerator and denominator by 4 yields 250/1, or 250.
Real-World Applications of Division
The seemingly simple operation of 1000 / 4 has wide-ranging applications in various fields:
-
Resource Allocation: Imagine distributing 1000 pencils equally among 4 classrooms. The solution, 250, tells us each classroom receives 250 pencils. This applies to numerous resource allocation scenarios, from dividing budgets to assigning tasks.
-
Unit Conversion: Division is crucial for converting units of measurement. For example, if you need to convert 1000 centimeters into meters (knowing there are 100 centimeters in a meter), you would divide 1000 by 100, resulting in 10 meters.
-
Average Calculation: Finding the average of four numbers involves adding the numbers and dividing the sum by 4. This principle extends to various statistical applications, such as calculating average scores, speeds, or temperatures.
-
Geometry and Measurement: Calculating the area of a rectangle requires multiplying length and width. The reverse process—dividing the area by one dimension—gives the other dimension. Similar applications are found in calculating volumes and other geometric properties.
-
Computer Science: Division is a fundamental arithmetic operation in computer programming used in countless algorithms and applications, including data processing, image manipulation, and game development.
-
Finance: Dividing total profits by the number of investors calculates each investor's share of profits. Similar applications exist in calculating interest rates, loan repayments, and other financial computations.
Beyond the Numbers: Mathematical Principles
Solving 1000 / 4 touches upon several important mathematical principles:
-
Factors and Multiples: The fact that 1000 is divisible by 4 indicates that 4 is a factor of 1000, and 1000 is a multiple of 4. Understanding factors and multiples is essential in number theory and algebra.
-
Prime Factorization: The prime factorization of 1000 is 2³ x 5³. The prime factorization of 4 is 2². This shows how the factors of the divisor (4) are contained within the factors of the dividend (1000), leading to a whole number quotient.
-
Divisibility Rules: Knowing divisibility rules can simplify calculations. The rule for divisibility by 4 states that a number is divisible by 4 if its last two digits are divisible by 4. Since 00 is divisible by 4, we know 1000 is divisible by 4.
-
Modular Arithmetic: The concept of remainders is central to modular arithmetic, used in cryptography, computer science, and various other fields. Although 1000/4 has no remainder, understanding remainders is crucial for solving problems where division isn't exact.
Expanding the Concept: Exploring Variations
Let's consider variations of the problem to further solidify our understanding:
-
1000 / 5: This is a simpler problem, easily solvable mentally (200). The solution reinforces the understanding of division as a process of equal sharing.
-
1000 / 0: This is undefined. Division by zero is not allowed in mathematics because it leads to inconsistencies and paradoxes.
-
1001 / 4: This introduces a remainder. Solving this problem (250 with a remainder of 1) helps to solidify the concept of handling remainders in division.
-
Larger Dividends and Divisors: Extending the problem to larger numbers, such as 10,000 / 4 or 1,000,000 / 4, strengthens the understanding of the division algorithm and the efficiency of various solution methods.
Frequently Asked Questions (FAQ)
-
What is the easiest way to solve 1000 / 4? For many, mental math (recognizing that 100/4 = 25, therefore 1000/4 = 250) is the quickest and easiest method.
-
What happens if the dividend is smaller than the divisor? If the dividend is smaller than the divisor, the quotient will be less than 1, often represented as a fraction or decimal.
-
Why is division by zero undefined? Division by zero is undefined because it leads to mathematical inconsistencies. Any number multiplied by zero is zero, so there's no number that, when multiplied by zero, will give a non-zero result.
-
What are some real-world examples where division with a remainder is important? Dividing 10 cookies equally among 3 children results in 3 cookies each, with one cookie remaining. Remainders are relevant in scenarios where exact division isn't possible, such as distributing resources, scheduling tasks, or optimizing processes.
Conclusion: The Significance of a Simple Equation
While seemingly simple, 1000 / 4 serves as a gateway to understanding fundamental mathematical concepts and their broad applications. From resource allocation to complex algorithms, the principle of division underpins numerous aspects of our world. Mastering this operation and its underlying principles is not merely about finding the correct answer (250) but also about developing a deeper appreciation for the power and elegance of mathematics. The ability to solve problems like 1000 / 4 efficiently and accurately is a cornerstone of mathematical literacy and a valuable skill applicable across various disciplines.
Latest Posts
Latest Posts
-
Half Of 30
Sep 13, 2025
-
20 Of 11
Sep 13, 2025
-
E 3 4
Sep 13, 2025
-
99 3kg In Stone
Sep 13, 2025
-
Biggest Digital Clock
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1000 / 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.