5x X 2
stanleys
Sep 13, 2025 · 6 min read
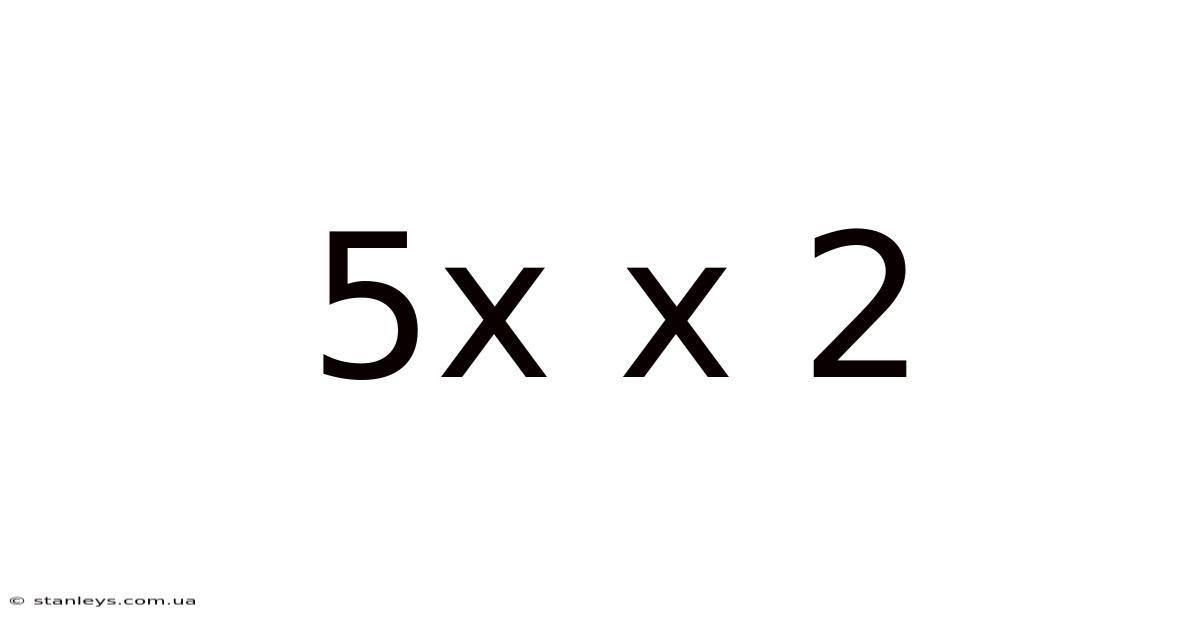
Table of Contents
Decoding 5x x 2: A Deep Dive into Multiplication and its Applications
Understanding the seemingly simple equation "5x x 2" unlocks a gateway to broader mathematical concepts and real-world applications. This article will explore this equation in depth, progressing from basic multiplication to more complex algebraic manipulations and practical examples. We'll cover various aspects, ensuring a comprehensive understanding suitable for students of various levels, from elementary school to high school and beyond.
Introduction: The Fundamentals of Multiplication
At its core, "5x x 2" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that signifies repeated addition. In this case, we're adding 5x to itself two times: 5x + 5x. The result is 10x. This might seem straightforward, but understanding the underlying principles allows us to tackle more intricate mathematical challenges. The "x" here represents a variable, a symbol representing an unknown value. This distinguishes it from a simple numerical multiplication like 5 x 2 = 10.
Step-by-Step Breakdown of 5x x 2
Let's break down the calculation step-by-step to reinforce the concept:
-
Identify the components: We have the coefficient 5, the variable x, and the multiplier 2.
-
Apply the multiplication: We multiply the coefficient (5) by the multiplier (2). This gives us 10.
-
Retain the variable: The variable x remains unchanged because we're not performing any operation on it beyond multiplication.
-
Final Result: Therefore, 5x x 2 = 10x
Expanding the Concept: Introduction to Algebra
The expression "5x x 2" is a fundamental concept in algebra. Algebra uses symbols, usually letters like x, y, or z, to represent unknown quantities or variables. These variables allow us to write general formulas and equations that can be applied to a wide range of situations.
-
Coefficients: The number in front of a variable (in this case, 5) is called the coefficient. It indicates how many times the variable is being multiplied.
-
Variables: The letters (x in this case) represent unknown values or quantities. The beauty of algebra lies in its ability to solve for these unknowns.
-
Constants: Constants are fixed numerical values that do not change (like the 2 in our equation).
Solving Equations with 5x x 2
Now let’s explore how "5x x 2" plays a part in solving equations. Imagine we have the following equation:
5x x 2 = 20
To solve for x, we follow these steps:
-
Simplify the left side: We already know that 5x x 2 simplifies to 10x. So our equation becomes: 10x = 20
-
Isolate the variable: To find the value of x, we need to isolate it. We do this by dividing both sides of the equation by the coefficient of x (which is 10): 10x/10 = 20/10
-
Solve for x: This simplifies to x = 2.
Therefore, in the equation 5x x 2 = 20, the value of x is 2.
Real-World Applications of 5x x 2 and Similar Equations
While seemingly simple, the concept underlying 5x x 2 has numerous real-world applications. Here are a few examples:
-
Geometry: Calculating the area of a rectangle. If the width of a rectangle is 5x and the length is 2, the area is 5x x 2 = 10x square units. If x represents a specific measurement (e.g., x = 3 meters), we can then calculate the precise area.
-
Cost Calculation: If an item costs 5x dollars and you buy two, the total cost is 5x x 2 = 10x dollars. Again, substituting a value for x allows for a specific cost calculation.
-
Physics: Many physics formulas involve multiplication. For example, if the speed of an object is 5x meters per second and it travels for 2 seconds, the total distance covered would be 5x x 2 = 10x meters.
-
Finance: Calculating simple interest. If the principal amount is 5x and the interest rate is 2% per annum, the interest earned in one year would be 5x x 0.02 = 0.1x.
Beyond the Basics: More Complex Scenarios
Let’s consider more complex scenarios involving 5x x 2:
-
Equations with multiple variables: Suppose we have the equation 5x x 2 + 3y = 17. Solving this would involve using algebraic manipulation to isolate either x or y, potentially requiring additional information or equations to find the values of both variables.
-
Equations with exponents: If we introduce exponents, such as (5x)² x 2, the solution would involve squaring (5x) first (resulting in 25x²) before multiplying by 2, yielding 50x².
-
Inequalities: Instead of an equals sign, we might have an inequality, such as 5x x 2 > 10. Solving this would involve finding the range of x values that satisfy the inequality (in this case, x > 1).
Expanding the Mathematical Landscape
The simple expression "5x x 2" provides a stepping stone to more advanced mathematical concepts. Understanding this fundamental operation lays the groundwork for:
-
Distributive Property: The distributive property states that a(b + c) = ab + ac. This can be applied to expressions involving 5x x 2 within a larger equation.
-
Factoring: Factoring is the process of breaking down an expression into smaller components. Understanding multiplication helps in reverse-engineering expressions to find their factors.
-
Polynomial Arithmetic: Polynomials are expressions consisting of variables and constants combined using addition, subtraction, and multiplication. Mastering basic multiplication like 5x x 2 is crucial for manipulating and solving polynomial equations.
Frequently Asked Questions (FAQ)
-
Q: What if the equation was 2 x 5x?
- A: Multiplication is commutative, meaning the order doesn't matter. 2 x 5x is the same as 5x x 2, both equaling 10x.
-
Q: Can x be a negative number?
- A: Yes, x can be any real number, including negative numbers. If x = -1, then 5x x 2 = 5(-1) x 2 = -10.
-
Q: What if there were more variables?
- A: The principle remains the same. If we had an equation like 5xy x 2, we would simply multiply the coefficients (5 x 2 = 10), leaving the variables as they are (10xy).
-
Q: How is this used in programming?
- A: This concept is fundamental in computer programming for creating algorithms and performing calculations. Variables and expressions like 5x x 2 are routinely used in programming languages to represent and manipulate data.
Conclusion: A Building Block for Mathematical Proficiency
The equation "5x x 2," while seemingly simplistic, serves as a crucial building block in the broader world of mathematics. Understanding its implications, from basic multiplication to algebraic manipulations and real-world applications, is essential for developing a strong mathematical foundation. By mastering these fundamental principles, students can confidently tackle more complex mathematical challenges and apply their knowledge across diverse fields. The seemingly simple act of multiplying 5x by 2 opens doors to a vast and exciting world of mathematical possibilities. Remember that consistent practice and a curious mindset are key to unlocking your full mathematical potential.
Latest Posts
Latest Posts
-
49 2kg In Stone
Sep 13, 2025
-
93 5kg In Stones
Sep 13, 2025
-
2 7x 4
Sep 13, 2025
-
55lbs In Stone
Sep 13, 2025
-
Standard Form Rules
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.