2 7x 4
stanleys
Sep 13, 2025 · 5 min read
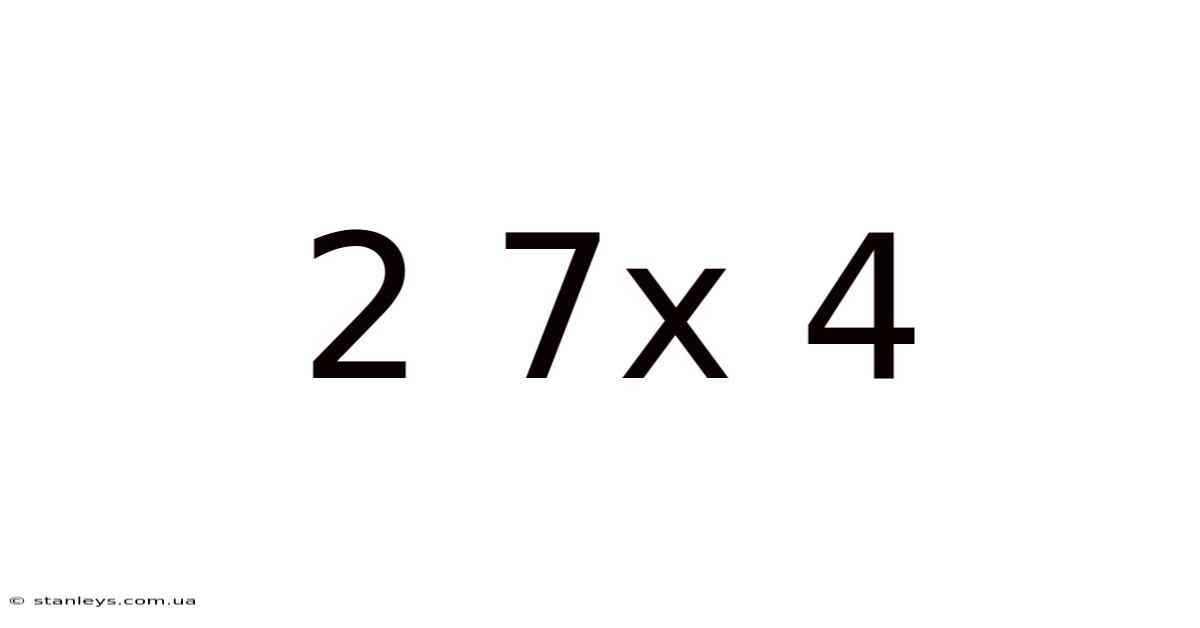
Table of Contents
Decoding 27 x 4: A Deep Dive into Multiplication and Beyond
This article delves into the seemingly simple mathematical problem of 27 multiplied by 4 (27 x 4). While the answer might seem readily apparent to many, we'll explore this calculation through various methods, uncovering underlying mathematical principles, and extending our understanding to broader concepts in arithmetic and beyond. This exploration will be beneficial for students learning multiplication, and also for those looking to refresh their foundational math skills. We'll cover multiple approaches, ensuring a comprehensive understanding suitable for diverse learning styles.
I. The Fundamentals: Understanding Multiplication
Before tackling 27 x 4 directly, let's establish a strong foundation in multiplication. Multiplication is essentially repeated addition. For example, 4 x 3 means adding 3 four times: 3 + 3 + 3 + 3 = 12. Therefore, 27 x 4 represents adding 27 four times.
II. Methods for Calculating 27 x 4
Several methods can be used to solve 27 x 4. We'll explore the most common and effective approaches:
A. Repeated Addition
The most basic method, as described above, involves adding 27 four times: 27 + 27 + 27 + 27 = 108. This method is straightforward but can be time-consuming for larger numbers.
B. Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this to break down 27 x 4 into smaller, more manageable calculations. We can rewrite 27 as 20 + 7:
4 x (20 + 7) = (4 x 20) + (4 x 7) = 80 + 28 = 108
C. Standard Multiplication Algorithm (Long Multiplication)
This is a common method taught in schools. It involves multiplying each digit of 27 by 4 individually and then adding the results:
27
x 4
-------
28 (4 x 7)
80 (4 x 20)
-------
108
This method systematically breaks down the multiplication into smaller steps, making it easier to manage larger numbers.
D. Lattice Multiplication
Lattice multiplication is a visual method that can be helpful for understanding the process of carrying over digits. A grid is drawn, and the calculation is performed within the grid's cells before summing the diagonal results.
E. Mental Math Techniques
With practice, you can perform this calculation mentally. One approach is to double 27 twice:
- 27 x 2 = 54
- 54 x 2 = 108
III. Extending the Understanding: Exploring Related Concepts
The simple calculation 27 x 4 opens doors to a wealth of mathematical concepts:
A. Factors and Multiples
In the equation 27 x 4 = 108, 27 and 4 are factors of 108, while 108 is a multiple of both 27 and 4. Understanding factors and multiples is crucial for various mathematical operations, including simplifying fractions and solving algebraic equations.
B. Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves). Let's find the prime factorization of 108:
108 = 2 x 54 = 2 x 2 x 27 = 2 x 2 x 3 x 9 = 2 x 2 x 3 x 3 x 3 = 2² x 3³
This decomposition is fundamental in simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM).
C. Order of Operations (PEMDAS/BODMAS)
The order of operations dictates the sequence in which calculations should be performed. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) helps remember the correct order. Understanding this is crucial when dealing with more complex equations involving multiple operations.
D. Algebraic Representation
The equation 27 x 4 = 108 can be represented algebraically as:
- 27a = 108, where 'a' represents 4. Solving for 'a' involves dividing both sides by 27: a = 108/27 = 4
E. Applications in Real-World Scenarios
Multiplication is ubiquitous in daily life. Consider these examples related to 27 x 4:
- Cost Calculation: If an item costs $27, and you buy 4 of them, the total cost is $108.
- Area Calculation: If a rectangle has a length of 27 units and a width of 4 units, its area is 108 square units.
- Measurement Conversion: If you have 27 groups of 4 items each, you have a total of 108 items.
IV. Addressing Potential Difficulties and Common Mistakes
While 27 x 4 is relatively simple, some students may encounter challenges:
- Carrying over digits: In long multiplication, accurately carrying over digits from one column to the next is crucial. Practice is key to mastering this skill.
- Place value: Understanding place value (ones, tens, hundreds, etc.) is fundamental for correctly performing multiplication.
- Mistakes in addition: Errors in addition can lead to incorrect final answers, especially in the repeated addition method. Careful and methodical addition is important.
V. Further Exploration and Practice
To enhance your understanding, consider these activities:
- Practice with similar problems: Try multiplying other two-digit numbers by single-digit numbers using various methods.
- Solve word problems: Create and solve word problems involving multiplication.
- Explore online resources: Several educational websites offer interactive exercises and tutorials on multiplication.
- Use manipulatives: Using concrete objects like blocks or counters can help visualize the multiplication process, especially for younger learners.
VI. Conclusion
The seemingly straightforward calculation of 27 x 4 provides a springboard for exploring fundamental mathematical concepts. From understanding the distributive property to prime factorization and real-world applications, this simple problem illuminates the broader landscape of arithmetic. Mastering multiplication not only helps in solving mathematical problems but also strengthens problem-solving skills applicable in numerous areas of life. By understanding the various methods and underlying principles, one gains a deeper appreciation for the elegance and utility of mathematics. Continuous practice and exploration will solidify your understanding and pave the way for tackling more complex mathematical challenges with confidence.
Latest Posts
Latest Posts
-
Manual Impact Driver
Sep 13, 2025
-
75 Of 45
Sep 13, 2025
-
Sugar Rush Vanellope
Sep 13, 2025
-
Odysseus With Bow
Sep 13, 2025
-
76 4kg In Stones
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 7x 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.