5000 / 3
stanleys
Sep 14, 2025 · 6 min read
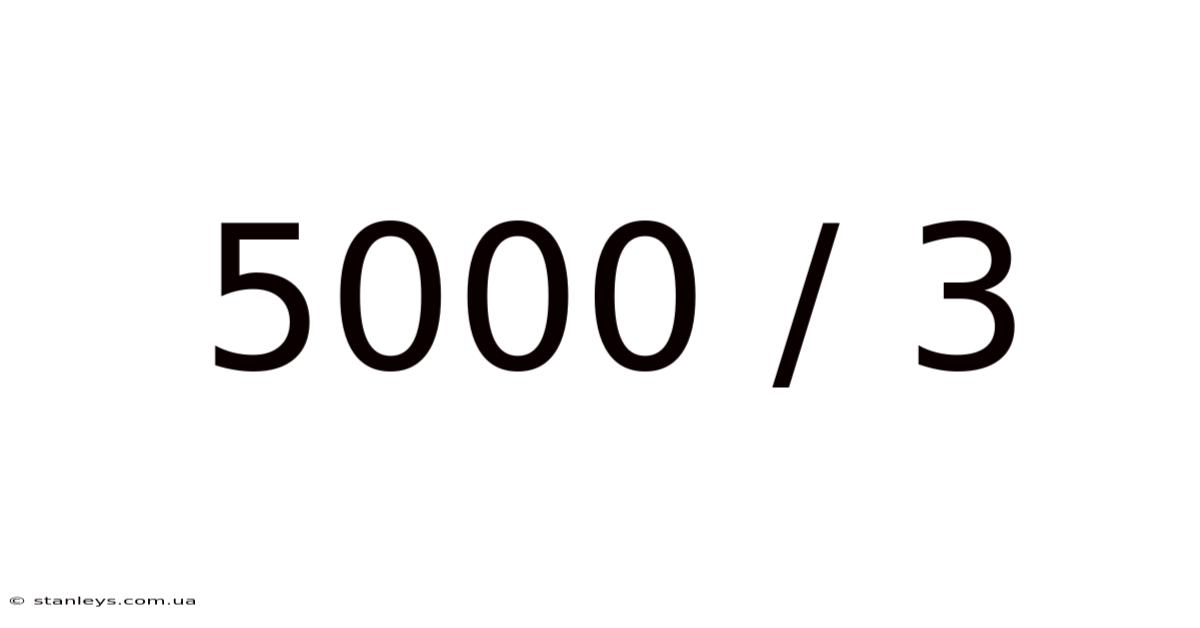
Table of Contents
Decoding 5000 / 3: A Deep Dive into Division and its Applications
This article explores the seemingly simple mathematical operation of 5000 divided by 3, delving beyond the basic answer to uncover the underlying concepts, practical applications, and related mathematical principles. Understanding this seemingly simple calculation unlocks a deeper appreciation for division, its importance in various fields, and its connection to broader mathematical concepts. We'll cover the process, explore different methods, discuss real-world examples, and address frequently asked questions.
I. The Fundamentals: Performing the Division
The most straightforward way to calculate 5000 / 3 is through long division. This method, while seemingly elementary, forms the bedrock of many more complex mathematical procedures. Let's walk through it step-by-step:
-
Set up the problem: Write 5000 as the dividend (the number being divided) and 3 as the divisor (the number you're dividing by).
-
Divide the thousands digit: 3 goes into 5 once (3 x 1 = 3). Write '1' above the 5 in the thousands place. Subtract 3 from 5, leaving 2.
-
Bring down the hundreds digit: Bring down the 0 from the hundreds place, creating the number 20.
-
Divide the tens digit: 3 goes into 20 six times (3 x 6 = 18). Write '6' above the 0 in the hundreds place. Subtract 18 from 20, leaving 2.
-
Bring down the tens digit: Bring down the next 0 from the tens place, creating the number 20.
-
Divide the tens digit (again): 3 goes into 20 six times (3 x 6 = 18). Write '6' above the 0 in the tens place. Subtract 18 from 20, leaving 2.
-
Bring down the ones digit: Bring down the final 0 from the ones place, creating the number 20.
-
Divide the ones digit (again): 3 goes into 20 six times (3 x 6 = 18). Write '6' above the 0 in the ones place. Subtract 18 from 20, leaving 2.
-
Remainder: The remaining 2 is the remainder.
Therefore, 5000 / 3 = 1666 with a remainder of 2. This can also be expressed as a mixed number: 1666 ⅔ or as a decimal: 1666.666... (the 6 repeating infinitely).
II. Alternative Methods: Exploring Different Approaches
While long division is a fundamental method, there are alternative approaches to solving 5000 / 3:
-
Using a calculator: The simplest and often fastest way is to use a calculator. Simply enter 5000 ÷ 3 and the calculator will provide the answer, typically displaying it as a decimal (1666.666...).
-
Breaking down the problem: We can simplify the calculation by breaking down 5000 into multiples of 3. For instance, we know that 3000 is divisible by 3 (3000/3 = 1000), and 2000 is approximately 666 times 3 with a remainder. Adding these results gives a close approximation. While less precise for this specific problem without further calculation, this method illustrates a useful problem-solving strategy.
-
Using fractions: The result can be expressed as the improper fraction 5000/3, which can then be converted into a mixed number (1666 ⅔) providing an exact representation of the quotient and remainder.
III. Real-World Applications: Where Division Matters
Division, exemplified by the calculation 5000/3, has countless real-world applications across diverse fields:
-
Resource Allocation: Imagine distributing 5000 kilograms of grain equally among 3 villages. The calculation 5000 / 3 determines how much grain each village receives (approximately 1666.67 kg). The remainder could represent a small amount to be handled separately or distributed fairly in other manner.
-
Engineering and Construction: Calculating the number of equally sized units (like bricks or tiles) needed to cover a specific area, or dividing total project costs amongst multiple contractors often involves division.
-
Finance and Budgeting: Dividing a total budget among different project expenses, or calculating the per-unit cost of a product based on bulk purchasing uses division principles.
-
Data Analysis: Averaging data sets, calculating rates, and determining proportions frequently use division. For example, calculating the average score of 3 exams with a total of 5000 points requires division.
-
Science and Measurement: Dividing total distance by time to calculate speed, or splitting a total sample weight into smaller parts for experiments often involves division.
-
Computer Science: Many algorithms and programming tasks use division and the modulus operator (%), which finds the remainder after a division. The concept of remainder is crucial in numerous programming applications.
IV. Beyond the Basics: Connecting to Broader Mathematical Concepts
The simple calculation 5000 / 3 provides a springboard to exploring deeper mathematical ideas:
-
Decimal Representation: The resulting decimal, 1666.666..., illustrates the concept of repeating decimals. These decimals, where a digit or sequence of digits repeat infinitely, are often a product of division where the divisor doesn't evenly divide the dividend.
-
Rational and Irrational Numbers: The result can be expressed as a rational number (a number that can be expressed as a fraction), namely 5000/3 or 1666 ⅔. This stands in contrast to irrational numbers, which cannot be expressed as a fraction, like π (pi).
-
Modular Arithmetic: The remainder of 2, after performing 5000/3, is significant in modular arithmetic. In modulo 3 arithmetic, 5000 is congruent to 2 (written as 5000 ≡ 2 (mod 3)). This concept is vital in cryptography and other advanced mathematical applications.
-
Approximation and Estimation: Understanding that 5000/3 is approximately 1667 allows for quick mental estimations in various scenarios, providing a valuable practical skill.
-
Algorithm Development: The process of long division itself can be viewed as a simple algorithm, which can be further generalized and applied to more complex division tasks.
V. Frequently Asked Questions (FAQ)
-
What is the exact value of 5000/3? The exact value is 1666 ⅔, or approximately 1666.666...
-
Why is there a remainder? There's a remainder because 5000 is not perfectly divisible by 3. 3 does not divide evenly into 5000.
-
How can I convert the remainder to a decimal? The remainder (2) can be expressed as a fraction (2/3), which, when divided, yields the repeating decimal 0.666... This is then added to the whole number part (1666) to get 1666.666...
-
What are the practical implications of the remainder? The remainder often represents a leftover or unused portion. In real-world situations, it might signify a small amount of material, resources, or funds remaining after an even distribution. Decisions must be made on how to allocate this extra or leftover portion.
-
Are there other ways to represent the answer besides decimal and fraction? Yes, the answer can be represented as a mixed number (1666 ⅔), as an improper fraction (5000/3), or using scientific notation (1.666... x 10³).
VI. Conclusion: The Significance of Simple Division
The seemingly basic calculation 5000 / 3 opens up a fascinating world of mathematical concepts and applications. From fundamental long division to the intricate workings of modular arithmetic and the practicality of real-world applications, this simple equation reveals the depth and breadth of mathematical principles. Understanding this calculation not only provides a precise answer but also empowers us to approach complex problems with a more nuanced and informed perspective. It highlights the importance of understanding the underlying principles, exploring alternative methods, and appreciating the pervasive nature of division in various facets of our lives. The seemingly straightforward answer of 1666.666... is actually a gateway to a deeper understanding of mathematics and its practical applications.
Latest Posts
Latest Posts
-
Megalodon Comparison Size
Sep 14, 2025
-
Autumn In Spanish
Sep 14, 2025
-
20 Of 380
Sep 14, 2025
-
Factorise 7y 21
Sep 14, 2025
-
Decimal Of 15
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5000 / 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.