20 Of 380
stanleys
Sep 14, 2025 · 7 min read
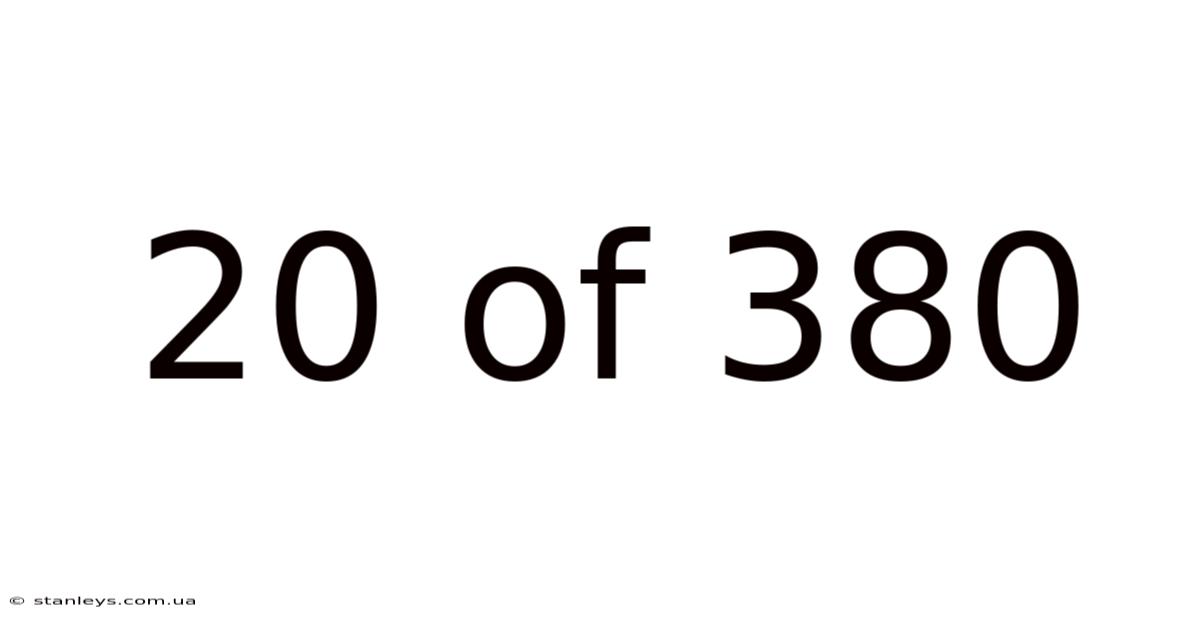
Table of Contents
Decoding the Enigma: Understanding the Significance of "20 of 380"
The phrase "20 of 380" might initially seem cryptic, lacking immediate context. However, depending on the application, it represents a powerful concept relating to probability, statistics, sampling, and even project management. This article delves deep into the meaning and implications of this seemingly simple ratio, exploring its relevance across various fields and unveiling its underlying significance. We'll explore how understanding this concept can improve your analytical skills and problem-solving abilities.
Understanding the Basic Ratio: What Does "20 of 380" Mean?
At its core, "20 of 380" is a simple fraction representing a part-to-whole relationship. It signifies that 20 units are selected or observed from a total population of 380 units. This seemingly basic ratio has profound implications across various disciplines, particularly in statistics and probability. The fraction can be simplified to 1/19, giving us a clearer picture of the proportion. This means that for every 19 units in the population, one unit is represented in the sample of 20.
Applications Across Disciplines: Where Does "20 of 380" Appear?
The application of this ratio varies greatly depending on the context. Let's explore some examples:
1. Statistical Sampling and Inference:
In statistics, "20 of 380" could represent a sample size drawn from a larger population. Researchers frequently use sampling techniques to draw conclusions about a larger group without needing to study every individual. The accuracy of these inferences depends heavily on the sampling method and the sample size. A sample of 20 from a population of 380 might be sufficient for certain analyses, particularly if the population is homogenous, but insufficient for others. The representativeness of the sample is crucial. A biased sample would lead to inaccurate conclusions, regardless of the size.
- Example: Imagine a company conducting a customer satisfaction survey. They have 380 customers, and they choose to survey 20 of them randomly. The responses from these 20 customers can be used to infer the overall satisfaction level of the entire customer base, but with a margin of error.
2. Quality Control and Acceptance Sampling:
In manufacturing and quality control, "20 of 380" could represent a batch of items inspected for defects. Inspecting every item is often impractical or costly, so a sample is inspected, and the results are extrapolated to the entire batch. If more than a certain percentage of the sample is defective, the entire batch might be rejected. The acceptable defect rate would be determined based on various factors, including the cost of inspection and the cost of defects.
- Example: A factory producing 380 electronic components might select 20 at random for testing. If more than a pre-determined percentage of these 20 components fail the test, the entire batch of 380 might be deemed faulty and require further investigation.
3. Project Management and Task Completion:
In project management, "20 of 380" could represent the progress of a project. If a project consists of 380 tasks, and 20 have been completed, it represents a progress of approximately 5.3%. This simple ratio offers a quick way to monitor project progress and identify potential delays.
- Example: A construction project involving 380 individual tasks might have 20 tasks completed. This allows project managers to track progress and identify potential bottlenecks.
4. Risk Assessment and Probability:
In risk assessment, "20 of 380" could represent the number of incidents occurring out of a total number of potential occurrences. This can be used to calculate the probability of an event happening. The probability of an incident in this case would be 20/380, or approximately 5.3%. This probability can be utilized to inform decisions regarding risk mitigation.
- Example: A company analyzing safety incidents might find that 20 accidents occurred out of 380 potential accident scenarios. This information informs risk management strategies.
The Importance of Context and Sample Size: Limitations of "20 of 380"
While "20 of 380" provides a numerical representation, its significance depends heavily on the context. The crucial factor is the sample size relative to the population size. A sample of 20 from a population of 380 might be considered small, especially if the population is heterogeneous (displays significant variability).
-
Sampling Bias: A small sample size increases the risk of sampling bias, where the sample doesn't accurately reflect the characteristics of the population. If the selection process isn't random or representative, the conclusions drawn from the sample might be misleading.
-
Margin of Error: A smaller sample size generally results in a larger margin of error when making inferences about the population. This means there's a greater chance that the results obtained from the sample differ significantly from the true values in the population.
-
Statistical Power: The statistical power of a study is its ability to detect a real effect if one exists. Small sample sizes often have low statistical power, meaning that even if a real effect exists, the study might fail to detect it.
Improving Interpretation: Considering Statistical Methods
To gain a more complete understanding of what "20 of 380" signifies, statistical methods are essential. For example, confidence intervals can be calculated to provide a range of values within which the true population parameter is likely to fall. Hypothesis testing can be used to determine whether the observed difference between the sample and the population is statistically significant.
-
Confidence Intervals: These provide a range of values within which the true population parameter (e.g., the mean or proportion) is likely to lie with a certain degree of confidence (e.g., 95%). A smaller sample size will result in a wider confidence interval, reflecting greater uncertainty.
-
Hypothesis Testing: This involves formulating a hypothesis about the population and testing it using the sample data. The p-value from a hypothesis test helps determine the statistical significance of the results. A smaller sample size makes it more difficult to reject the null hypothesis, even if there's a real effect.
Beyond Simple Ratios: Exploring Further Implications
The understanding of "20 of 380" extends beyond simple ratios. It underscores the importance of:
-
Data Analysis: The ability to extract meaning from numerical data is crucial in making informed decisions across various domains. Analyzing the ratio "20 of 380" requires a thorough understanding of the context and the application of statistical methods.
-
Critical Thinking: Critically evaluating the information presented and understanding the limitations of the data is essential. A simple ratio like "20 of 380" shouldn't be interpreted in isolation but within the larger context of the situation.
-
Quantitative Reasoning: The ability to interpret and use numerical information effectively is a critical skill in many professions. Understanding "20 of 380" requires understanding basic mathematical concepts and their application in real-world situations.
Frequently Asked Questions (FAQ)
Q: Can I always extrapolate findings from a sample of 20 out of 380 to the entire population?
A: No. The accuracy of extrapolating from a sample to the population depends on many factors, including the sampling method, the homogeneity of the population, and the desired level of precision. A larger sample size generally leads to more reliable extrapolations.
Q: What if the 20 selected items are not representative of the entire 380?
A: If the sample is not representative (biased), any conclusions drawn from it will likely be inaccurate. This highlights the critical importance of using appropriate sampling methods to ensure the sample accurately reflects the population.
Q: What statistical tests are suitable for analyzing data from a sample of 20 out of 380?
A: The appropriate statistical test depends on the type of data and the research question. For proportions, tests like the z-test or chi-square test might be appropriate. For means, a t-test could be used. The small sample size, however, will limit the statistical power of these tests.
Conclusion: The Enduring Relevance of "20 of 380"
While seemingly insignificant at first glance, "20 of 380" represents a fundamental concept in statistics, probability, and various other fields. Its interpretation hinges heavily on the context and the application of appropriate statistical methods. Understanding its implications requires not only mathematical proficiency but also critical thinking and a deep understanding of the limitations of sample data. By incorporating a robust understanding of statistical principles and sampling techniques, we can move beyond a simple ratio and extract meaningful insights from such data, empowering us to make more informed decisions in various aspects of life and work. Remember, the true value lies not just in the numbers, but in their informed interpretation.
Latest Posts
Latest Posts
-
50 Meters Yards
Sep 14, 2025
-
1 78m In Ft
Sep 14, 2025
-
23 Multiplication Table
Sep 14, 2025
-
10 Of 64
Sep 14, 2025
-
5 7 Of 134
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 380 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.