5 6 24
stanleys
Sep 17, 2025 · 6 min read
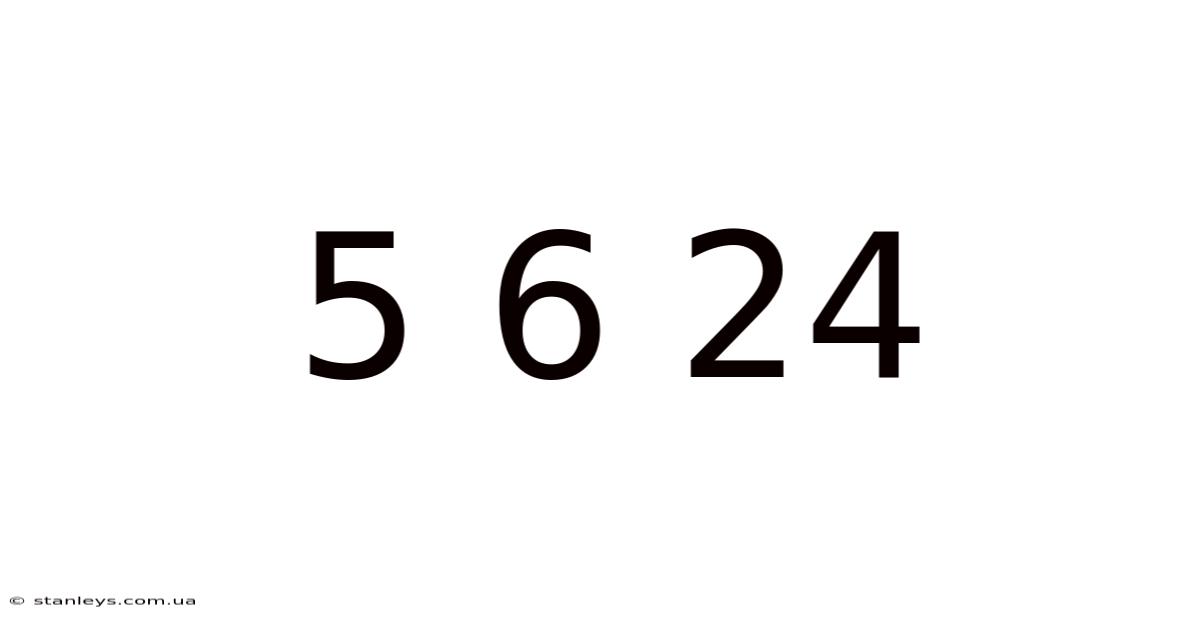
Table of Contents
Unlocking the Mysteries of 5, 6, and 24: A Deep Dive into Number Relationships
The seemingly simple numbers 5, 6, and 24 hold a surprising depth of mathematical relationships and interconnectedness. This exploration delves into their properties, revealing connections through prime factorization, divisibility rules, geometric interpretations, and their appearances in various mathematical contexts. Understanding these relationships enhances our appreciation for the intricate beauty and underlying structure of mathematics. We'll unravel the mysteries behind these numbers, demonstrating how seemingly disparate concepts converge to create a cohesive mathematical narrative.
I. Introduction: A First Look at 5, 6, and 24
At first glance, 5, 6, and 24 appear as disparate integers. However, a closer examination unveils a rich tapestry of mathematical connections. 5 is a prime number, meaning it's only divisible by 1 and itself. 6 is the smallest perfect number, the sum of its proper divisors (1, 2, and 3) equaling itself. 24 is a highly composite number, possessing a large number of divisors, and it plays a significant role in various mathematical areas, including combinatorics and geometry. This article will dissect these individual properties and then explore their intertwined relationships.
II. Prime Factorization and Divisibility: Unveiling the Building Blocks
Understanding the prime factorization of each number is crucial to grasping their connections.
-
5: The prime factorization of 5 is simply 5. Being a prime number, it's a fundamental building block in number theory.
-
6: The prime factorization of 6 is 2 x 3. This reveals that 6 is composed of the first two prime numbers.
-
24: The prime factorization of 24 is 2³ x 3. This shows that 24 contains three factors of 2 and one factor of 3. This factorization is key to understanding its numerous divisors.
The divisibility rules further illuminate their properties. A number is divisible by 5 if its last digit is 0 or 5. A number is divisible by 6 if it's divisible by both 2 and 3 (meaning its last digit is even and the sum of its digits is divisible by 3). 24 satisfies both conditions, highlighting its divisibility by both 2 and 3.
III. Geometric Interpretations: Visualizing Number Relationships
Geometry offers another lens through which to view these numbers.
-
5: A regular pentagon, a five-sided polygon with equal sides and angles, demonstrates the unique properties of the number 5 in geometric shapes. The angles and symmetries of a pentagon are intrinsically linked to the number 5.
-
6: The hexagon, a six-sided polygon, is a highly symmetrical shape found frequently in nature, from honeycombs to snowflakes. Its internal angles and area calculations directly involve the number 6.
-
24: 24 appears in various geometric contexts. For example, it's related to the number of faces, vertices, and edges in certain polyhedra. Consider a cube: it has 6 faces, 12 edges, and 8 vertices. The number 24 emerges in calculations involving the surface area and volume of more complex geometric solids.
IV. Number Theory Connections: Exploring Deeper Relationships
Delving into more advanced number theory reveals further connections between 5, 6, and 24.
-
Modular Arithmetic: Exploring these numbers within modular arithmetic, particularly modulo 5 and modulo 6, reveals patterns and congruences. For instance, considering remainders when dividing by 5, we observe cyclical patterns. Similarly, modulo 6 reveals different cyclical properties. These patterns are fundamental to cryptography and other advanced mathematical applications.
-
Combinatorics: The number 24 plays a significant role in combinatorics. It represents the number of permutations of four distinct objects (4!). This connection highlights the importance of 24 in counting problems and arrangements.
-
Number of Divisors: The number of divisors for each number is also significant. 5 has 2 divisors (1 and 5). 6 has 4 divisors (1, 2, 3, and 6). 24 has a significantly larger number of divisors (1, 2, 3, 4, 6, 8, 12, and 24), making it a highly composite number. This property is crucial in various number-theoretic analyses.
V. Appearances in Different Mathematical Contexts: A Wider Perspective
Beyond basic number theory, 5, 6, and 24 appear in various mathematical contexts.
-
Fibonacci Sequence: While not directly present in the sequence, numbers closely related to 5 and 6 frequently appear within the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, 34...). The relationships between consecutive Fibonacci numbers are a rich area of study.
-
Geometry and Trigonometry: The numbers 5 and 6 are prominently featured in geometric formulas and trigonometric identities, particularly concerning angles and shapes. For example, regular pentagons and hexagons provide numerous applications of these numbers.
-
Calculus and Analysis: Although not as directly involved as in other areas, these numbers may subtly appear in various calculations and approximations within calculus and mathematical analysis.
-
Algebra: The numbers 5, 6, and 24 can feature as coefficients or constants in algebraic equations and systems of equations, highlighting their role in algebraic structures and solutions.
VI. Solving Problems Involving 5, 6, and 24: Practical Applications
Let’s consider some practical examples involving these numbers.
Example 1: Divisibility: Determine if a number like 123,456 is divisible by 6. We can use the divisibility rule for 6: check if it’s divisible by both 2 and 3. Since the last digit is even (6), it’s divisible by 2. The sum of its digits (1+2+3+4+5+6 = 21) is divisible by 3. Therefore, 123,456 is divisible by 6.
Example 2: Combinatorics: How many ways can you arrange 4 different colored balls in a row? This is a permutation problem solved using factorials. The answer is 4! = 24.
Example 3: Geometry: Calculate the area of a regular hexagon with side length of 5 units. The formula involves the number 6, and the calculation will utilize the side length (5).
VII. Frequently Asked Questions (FAQs)
Q: Are 5, 6, and 24 related in any special way beyond their basic mathematical properties?
A: While there isn't a single, overarching, universally recognized relationship, their interwoven appearances in different mathematical branches highlight their interconnectedness. Their prime factorizations, divisibility rules, and roles in geometry and combinatorics reveal their subtle, yet significant, connections.
Q: Are there any advanced mathematical concepts that directly link these three numbers?
A: While not directly linked through a single, well-known theorem or concept, the numbers appear in various areas like modular arithmetic, group theory (via the symmetries of geometric shapes related to 6), and representation theory (via the divisors of 24 and their connections to group actions). However, these connections require a deep understanding of advanced mathematical concepts.
Q: Could there be undiscovered deeper mathematical relationships involving 5, 6, and 24?
A: It's entirely possible. Mathematics is a vast and ever-evolving field. New discoveries and deeper connections between seemingly disparate numbers are constantly being made. The relationships between 5, 6, and 24 may be further explored and potentially reveal new insights in the future.
VIII. Conclusion: A Holistic View of Number Relationships
This in-depth exploration has revealed the surprisingly rich relationships between the numbers 5, 6, and 24. From their prime factorizations and divisibility properties to their geometric interpretations and appearances in combinatorics and number theory, these numbers demonstrate the intricate web of connections within mathematics. By examining their properties individually and collectively, we’ve gained a deeper appreciation for the beauty and complexity of the mathematical world. The journey through these numbers is a testament to the elegance and interconnectedness that underpin mathematical concepts, constantly revealing new avenues for exploration and discovery. Further investigation into these numbers and their relationships promises to unveil even deeper mathematical truths.
Latest Posts
Latest Posts
-
Slingshot Bart Simpson
Sep 18, 2025
-
Tomorrows Or Tomorrows
Sep 18, 2025
-
60 Of 15
Sep 18, 2025
-
88kilos In Stone
Sep 18, 2025
-
Crown Tattoo Princess
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 6 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.