60 Of 15
stanleys
Sep 18, 2025 · 5 min read
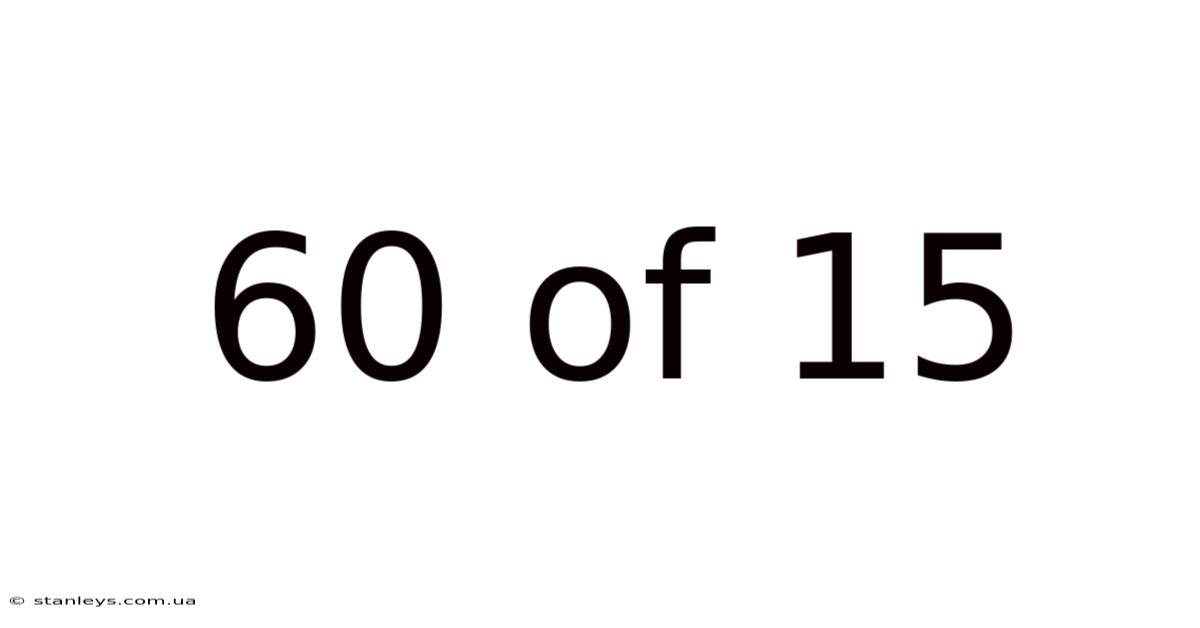
Table of Contents
Decoding the Fraction: Understanding 60/15 and its Implications
This article delves into the seemingly simple fraction 60/15, exploring its mathematical significance, practical applications, and broader implications within the world of numbers. We'll move beyond the simple calculation to uncover the underlying principles and how understanding this fraction can enhance your mathematical intuition. Understanding fractions like 60/15 is fundamental to grasping more complex mathematical concepts. We'll cover everything from basic simplification to its representation in different contexts, making this a comprehensive guide for learners of all levels.
Introduction: What is 60/15?
At its core, 60/15 is a fraction representing a part-to-whole relationship. It signifies 60 parts out of a total of 15 parts. This immediately suggests that something isn't quite right – we have more parts than the whole. This apparent paradox highlights the importance of understanding fractional representation and its limitations. While seemingly illogical at first glance, this seemingly contradictory fraction offers a valuable opportunity to explore the concepts of improper fractions and their conversion to mixed numbers.
Simplifying 60/15: Finding the Greatest Common Divisor (GCD)
Before we delve into interpretations, let's simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (60) and the denominator (15). The GCD is the largest number that divides both 60 and 15 without leaving a remainder.
One method to find the GCD is through prime factorization:
- 60: 2 x 2 x 3 x 5
- 15: 3 x 5
The common prime factors are 3 and 5. Multiplying these together gives us a GCD of 15.
Now, we divide both the numerator and the denominator by the GCD:
60 ÷ 15 = 4 15 ÷ 15 = 1
Therefore, the simplified fraction is 4/1, which is equivalent to 4. This means that 60/15 represents the whole number 4. This seemingly simple calculation reveals a fundamental aspect of fractions – their ability to represent whole numbers as well as parts of wholes.
Representing 60/15: Improper Fractions and Mixed Numbers
60/15 is an example of an improper fraction. An improper fraction is one where the numerator is greater than or equal to the denominator. Improper fractions often represent quantities greater than or equal to one whole unit. In this case, it represents exactly four whole units.
We can also express this as a mixed number. A mixed number combines a whole number and a proper fraction. Since 60/15 simplifies to 4, the equivalent mixed number is simply 4. There is no fractional component because the simplification results in a whole number. The absence of a fractional component highlights the concept of complete units.
Real-World Applications: Understanding Context
The fraction 60/15, while seemingly abstract, finds practical application in numerous real-world scenarios. Consider these examples:
-
Sharing Equally: Imagine 60 candies to be shared equally among 15 children. Each child receives 60/15 = 4 candies. This demonstrates the concept of division and fair distribution.
-
Measurement and Conversion: If you have a 60-meter long rope and need to cut it into 15 equal pieces, each piece will be 60/15 = 4 meters long. This highlights the application of fractions in measurement and unit conversions.
-
Ratio and Proportion: The fraction can represent a ratio. For instance, if a recipe calls for 60 grams of flour for every 15 grams of sugar, the ratio of flour to sugar is 60/15 = 4:1. This illustrates the importance of fractions in understanding proportions and scaling recipes.
-
Data Analysis and Statistics: In statistical analysis, 60/15 could represent a proportion within a dataset. For instance, if 60 out of 150 participants responded positively to a survey question, the proportion of positive responses is 60/150, which simplifies to 2/5 or 0.4. This highlights the application of fractions in expressing probabilities and proportions in data analysis.
These examples illustrate the versatility of fractions in real-world problem-solving, reinforcing the importance of understanding their meaning and manipulation.
Beyond the Basics: Extending the Concept
Understanding 60/15 opens doors to more complex mathematical concepts:
-
Decimal Representation: The fraction 60/15 is equivalent to the decimal number 4.0. This highlights the relationship between fractions and decimals, allowing for easier comparison and calculation in certain contexts.
-
Percentage: The fraction can be expressed as a percentage. Since 60/15 = 4, it is equivalent to 400%. This highlights the application of fractions in representing proportions as percentages.
-
Algebraic Expressions: Fractions like 60/15 can be incorporated into algebraic expressions and equations. For example, solving an equation like x/15 = 4 would lead to the solution x = 60. This demonstrates the use of fractions within more advanced mathematical contexts.
Frequently Asked Questions (FAQ)
-
Q: What happens if the denominator is zero?
- A: Division by zero is undefined in mathematics. A fraction with a denominator of zero is meaningless and has no numerical value.
-
Q: Are all improper fractions equal to whole numbers?
- A: No. While 60/15 simplifies to a whole number, many improper fractions simplify to mixed numbers (a whole number and a proper fraction). For example, 7/2 simplifies to 3 1/2.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand and work with. It helps in comparisons and calculations, and it presents the information in its most concise form.
-
Q: Can I use a calculator to simplify fractions?
- A: Yes, many calculators have functions to simplify fractions. However, understanding the underlying principles of finding the GCD is crucial for a deeper mathematical understanding.
Conclusion: The Significance of 60/15
While seemingly straightforward, the fraction 60/15 provides a rich learning opportunity. It demonstrates the fundamental concepts of simplification, improper fractions, mixed numbers, and their applications in various real-world scenarios. Understanding this simple fraction lays a solid foundation for tackling more complex mathematical problems and strengthens your numerical intuition. It underscores the importance of understanding not only the mechanics of calculations but also the underlying concepts and their practical implications. By exploring this seemingly simple fraction, we gain a deeper appreciation for the power and versatility of mathematics in understanding and interacting with the world around us. Furthermore, the ability to easily simplify and interpret fractions like 60/15 is a crucial skill for success in higher-level mathematics and related fields. The core principles learned here are applicable to a wide range of mathematical challenges, making this exploration a valuable investment in your mathematical understanding.
Latest Posts
Latest Posts
-
27cm To Mm
Sep 18, 2025
-
1 66m To Ft
Sep 18, 2025
-
Boggs Hunger Games
Sep 18, 2025
-
2 75 To Fraction
Sep 18, 2025
-
Bench Wheel Grinder
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.