3x 1 7
stanleys
Sep 18, 2025 · 6 min read
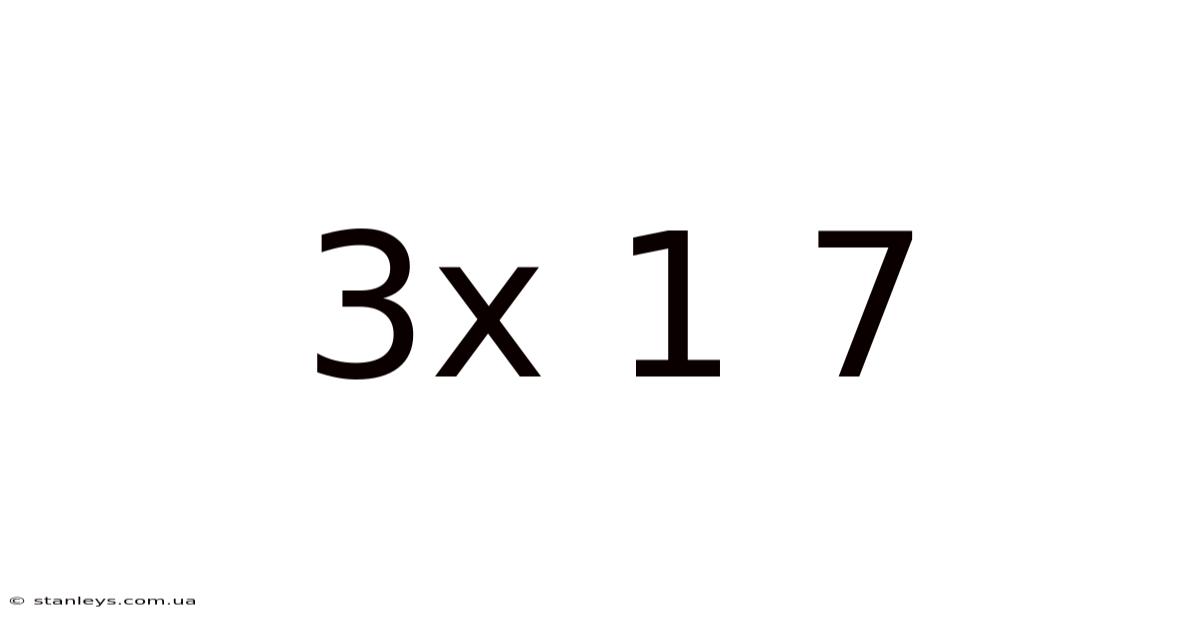
Table of Contents
Decoding the Enigma: Exploring the Mathematical and Symbolic Significance of "3x + 1 = 7"
The seemingly simple equation, 3x + 1 = 7, while elementary in its structure, opens a door to a fascinating exploration of mathematical concepts, problem-solving strategies, and even symbolic interpretations. This article delves into the depths of this equation, examining its solution, its place within broader mathematical frameworks, and its potential for deeper meaning beyond its straightforward arithmetic.
Introduction: Unraveling the Mystery
At first glance, 3x + 1 = 7 appears to be a trivial algebraic equation solvable by even a middle school student. However, it serves as a perfect microcosm of larger mathematical principles. Solving this equation not only provides a numerical answer but also introduces fundamental concepts like variables, coefficients, and the process of isolating a variable. Understanding this seemingly simple problem lays a crucial foundation for tackling more complex equations and mathematical challenges. This exploration will go beyond the simple solution, delving into the methodology, broader mathematical context, and even potential symbolic interpretations.
Solving the Equation: A Step-by-Step Guide
The beauty of this equation lies in its straightforward solvability. Let's break down the process step-by-step:
-
Isolate the term with 'x': Our goal is to get 'x' by itself on one side of the equation. To do this, we first subtract 1 from both sides:
3x + 1 - 1 = 7 - 1
This simplifies to:
3x = 6
-
Solve for 'x': Now, we need to isolate 'x' by dividing both sides of the equation by 3:
3x / 3 = 6 / 3
This gives us the solution:
x = 2
Therefore, the value of x that satisfies the equation 3x + 1 = 7 is 2. This seemingly simple process showcases the core principles of algebraic manipulation: maintaining balance through consistent operations on both sides of the equation.
Expanding the Horizon: Linear Equations and Their Significance
The equation 3x + 1 = 7 falls under the category of linear equations. Linear equations are characterized by having the highest power of the variable (in this case, x) being 1. They represent a straight line when graphed on a coordinate plane. Understanding linear equations is fundamental to many areas of mathematics and science, including:
- Physics: Modeling relationships between variables like distance, time, and velocity.
- Economics: Representing supply and demand curves, cost functions, and budget constraints.
- Computer Science: Developing algorithms and solving optimization problems.
- Engineering: Analyzing systems and predicting behavior based on linear relationships.
The simple equation 3x + 1 = 7 provides a solid introduction to the broader world of linear equations and their extensive applications.
Beyond the Numbers: Exploring Symbolic Interpretations
While the mathematical solution is straightforward, we can explore potential symbolic interpretations of the equation. The numbers themselves might hold symbolic weight depending on the context. For instance:
- The number 3: Often associated with the Holy Trinity in religious contexts, or representing completeness or wholeness in various cultures.
- The number 7: A significant number across many religious and cultural traditions, often linked to perfection, luck, or spirituality.
- The number 1: Symbolizing unity, beginnings, or a singular entity.
Interpreting the equation symbolically requires context and depends heavily on individual perspectives and beliefs. It’s important to note that these symbolic interpretations are not inherent to the mathematical equation itself but are imposed upon it based on external cultural or religious associations.
Extending the Concept: Variations and Generalizations
We can explore variations of the equation to further our understanding. For example, we could consider:
- Changing the coefficient: What if the equation was 5x + 1 = 7? The solution would change accordingly, illustrating the impact of the coefficient on the variable’s value.
- Changing the constant: What if the equation was 3x + 2 = 7? Again, this alters the solution, highlighting the role of the constant term.
- Introducing more variables: Moving beyond simple linear equations introduces complexities and requires more advanced techniques to solve.
By examining these variations, we can further solidify our grasp of algebraic manipulation and develop a deeper intuitive understanding of how different components of an equation influence its solution.
Connecting to Real-World Applications: Practical Examples
While the equation itself might seem abstract, it underpins many real-world applications. Consider these scenarios:
- Pricing strategies: A retailer might use a similar equation to determine the selling price of an item after adding a markup to the cost price. The 'x' could represent the cost price, and the equation would help calculate the selling price.
- Resource allocation: Imagine distributing resources proportionally. A simplified model might use a linear equation to allocate resources based on a certain ratio.
- Scientific measurements: Many scientific measurements and relationships are modeled using linear equations. Understanding this foundational concept allows for accurate interpretation and predictions.
While these examples are simplified, they demonstrate the practical relevance of understanding linear equations and their applications in various fields.
Frequently Asked Questions (FAQ)
-
Q: What if I get a fraction or a decimal as a solution? A: That's perfectly acceptable! Solutions to linear equations can be whole numbers, fractions, or decimals. The method of solving remains the same.
-
Q: Can this equation be represented graphically? A: Yes! A linear equation like 3x + 1 = 7 can be represented as a straight line on a coordinate plane. The solution (x = 2) represents the x-intercept of that line.
-
Q: Are there more complex equations similar to this one? A: Yes! This is a very simple linear equation. There are much more complex equations, including quadratic equations (where the highest power of the variable is 2), cubic equations (power 3), and many others, requiring more advanced solution techniques.
-
Q: What if the equation has no solution? A: Some equations might not have any solutions. For example, an equation like 3x + 1 = 3x + 5 has no solution because there is no value of x that can make the left side equal to the right side.
Conclusion: The Enduring Power of Simple Equations
The equation 3x + 1 = 7, while seemingly simple, serves as a powerful gateway into the world of mathematics. It introduces fundamental concepts, highlights problem-solving strategies, and even allows for symbolic interpretations. Its simplicity belies its depth, offering a glimpse into the vast and interconnected realm of mathematical principles and their real-world applications. From understanding linear equations to grasping the importance of algebraic manipulation, this seemingly simple equation provides a solid foundation for further exploration and deeper mathematical understanding. The ability to solve and interpret such equations is a crucial skill, applicable far beyond the classroom, providing valuable tools for navigating various aspects of life and problem-solving in various disciplines. Its enduring power lies in its ability to teach fundamental concepts in an accessible and engaging manner.
Latest Posts
Latest Posts
-
90 Of 2000
Sep 18, 2025
-
Plastic Cable Covering
Sep 18, 2025
-
Large Body Habitus
Sep 18, 2025
-
X 2 49
Sep 18, 2025
-
Slippery Dick Fish
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3x 1 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.