10 Of 320
stanleys
Sep 16, 2025 · 5 min read
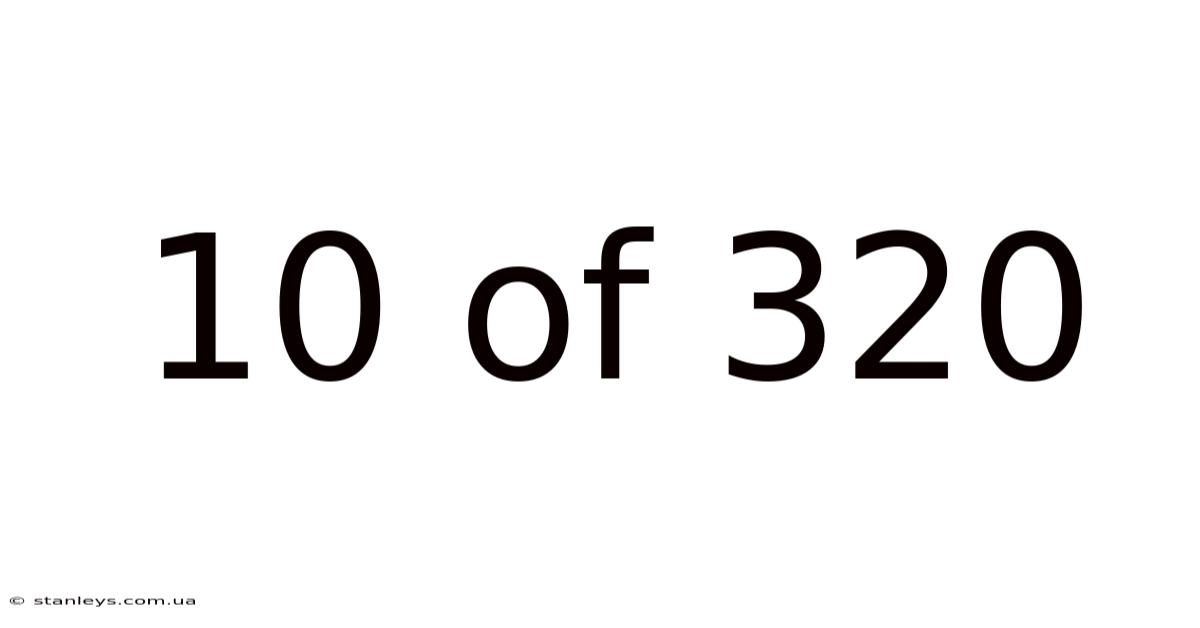
Table of Contents
Decoding the Mystery: Understanding the Fraction 10/320 and its Simplification
The seemingly simple fraction 10/320 might appear straightforward at first glance, but it holds within it the potential for a deeper understanding of fundamental mathematical concepts, particularly fraction simplification and the relationship between numerators and denominators. This article will delve into a comprehensive exploration of 10/320, guiding you through the process of simplification, highlighting the underlying mathematical principles, and addressing common misconceptions. We'll even explore real-world applications to solidify your understanding.
Introduction: What Does 10/320 Represent?
The fraction 10/320 represents a part of a whole. The numerator (10) indicates the number of parts we have, while the denominator (320) signifies the total number of equal parts that make up the whole. Imagine a pizza cut into 320 slices; 10/320 represents having 10 of those slices. This fraction, however, is not in its simplest form. Simplifying fractions is crucial for easier understanding and comparison, and that's where our journey begins.
Step-by-Step Simplification of 10/320
Simplifying a fraction involves finding the greatest common divisor (GCD) of the numerator and the denominator, and then dividing both by the GCD. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Let's break down the simplification of 10/320:
-
Find the factors of the numerator (10): The factors of 10 are 1, 2, 5, and 10.
-
Find the factors of the denominator (320): The factors of 320 are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, and 320.
-
Identify the greatest common divisor (GCD): By comparing the factors, we see that the largest number that divides both 10 and 320 is 10. Therefore, the GCD of 10 and 320 is 10.
-
Divide both the numerator and the denominator by the GCD:
10 ÷ 10 = 1 320 ÷ 10 = 32
-
The simplified fraction: The simplified form of 10/320 is therefore 1/32.
This means that 10/320 and 1/32 represent the same value; they are equivalent fractions. Using the simplified fraction makes calculations and comparisons much easier.
Mathematical Principles Behind Fraction Simplification
The process of simplifying fractions relies on the fundamental principles of division and equivalent fractions. When we divide both the numerator and the denominator by their GCD, we are essentially dividing the fraction by 1 (since GCD/GCD = 1). Dividing a fraction by 1 does not change its value, only its representation. This is a crucial concept in mathematics. We are not changing the value of the fraction, only expressing it in a more concise and manageable way.
Beyond the Basics: Prime Factorization and GCD
Finding the GCD can be simplified using prime factorization. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves). Let's apply this to our example:
- Prime factorization of 10: 2 x 5
- Prime factorization of 320: 2 x 2 x 2 x 2 x 2 x 2 x 5 (or 2<sup>6</sup> x 5)
By comparing the prime factorizations, we can see that both 10 and 320 share a common factor of 2 and 5. The GCD is the product of the common prime factors raised to the lowest power they appear in either factorization. In this case, it's 2<sup>1</sup> x 5<sup>1</sup> = 10. This method is particularly useful when dealing with larger numbers.
Real-World Applications of Fraction Simplification
Understanding fraction simplification is not just an academic exercise; it has practical applications in numerous areas of life:
-
Cooking and Baking: Recipes often involve fractions. Simplifying fractions ensures accurate measurements and consistent results.
-
Construction and Engineering: Precise measurements are vital, and simplifying fractions aids in accurate calculations and estimations.
-
Finance and Budgeting: Managing finances often involves dealing with portions of a whole (e.g., calculating percentages, splitting bills). Simplifying fractions helps with easier understanding and calculations.
-
Data Analysis and Statistics: Data is frequently represented using fractions and percentages. Simplifying fractions makes the data more manageable and easier to interpret.
Frequently Asked Questions (FAQ)
-
Q: Is there more than one way to simplify a fraction?
- A: Yes, you can simplify a fraction in multiple steps by dividing by common factors repeatedly until you reach the simplest form. However, using the GCD method is the most efficient way.
-
Q: What if the numerator and denominator have no common factors other than 1?
- A: The fraction is already in its simplest form. For example, 7/11 cannot be simplified further.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It provides a clearer and more concise representation of the value.
-
Q: Can a fraction be simplified if the denominator is a prime number and the numerator is not a multiple of the denominator?
- A: Yes, but only if the numerator and the denominator share a common factor, other than 1. If the denominator is a prime number, and the numerator is not a multiple of it, the fraction is already in its simplest form. For example 5/7 is already in its simplest form.
Conclusion: Mastering Fraction Simplification
Understanding and mastering fraction simplification is a cornerstone of mathematical literacy. The seemingly simple fraction 10/320 provides a valuable opportunity to explore the underlying principles of equivalent fractions, the greatest common divisor, and prime factorization. By applying these techniques, you can confidently simplify any fraction and apply this knowledge to various real-world scenarios. Remember, practice is key! The more you work with fractions, the more intuitive the process of simplification will become. So, grab a pencil and paper, and start practicing! You'll find that the ability to confidently simplify fractions will greatly enhance your mathematical skills and understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 Of 320 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.