40 Of 900
stanleys
Sep 11, 2025 · 6 min read
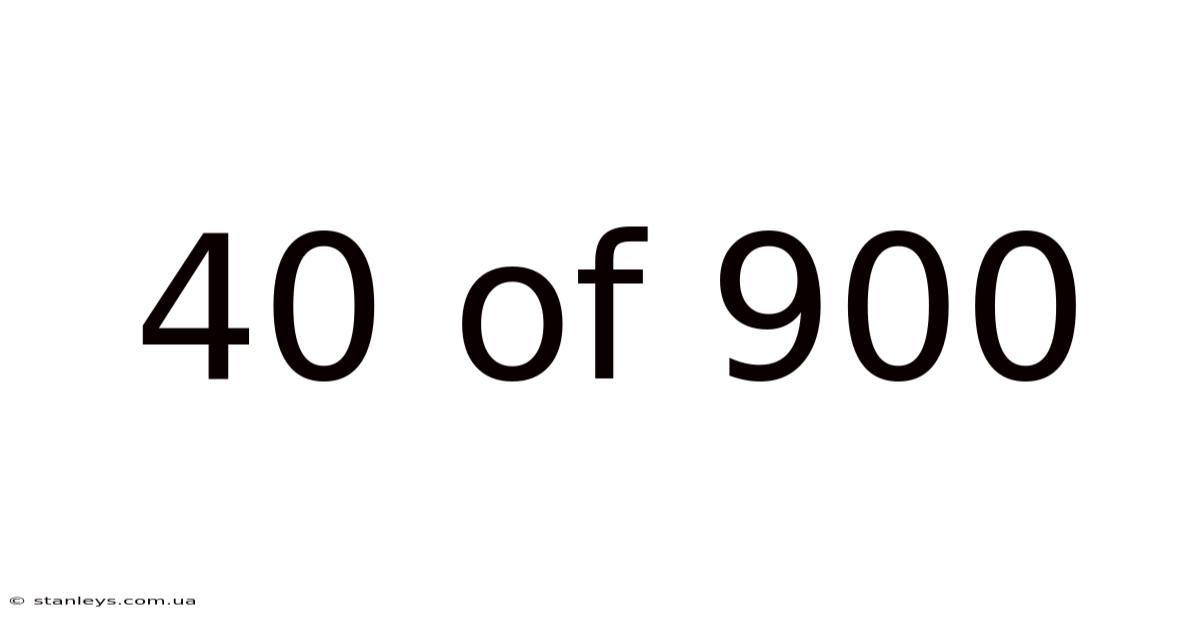
Table of Contents
Decoding the Mystery: Understanding the Fraction 40/900 and its Applications
The seemingly simple fraction 40/900 might appear insignificant at first glance. However, understanding this fraction and its various representations unlocks a world of mathematical concepts and practical applications. This article delves deep into the simplification, decimal conversion, percentage representation, and real-world uses of 40/900, ensuring a thorough understanding for readers of all levels. We'll explore its significance in areas ranging from basic arithmetic to more complex mathematical problems and practical scenarios.
Introduction: The Significance of Simplifying Fractions
Before we dive into the specifics of 40/900, it's crucial to understand the importance of simplifying fractions. A simplified fraction, also known as a fraction in its lowest terms, represents the same value as the original fraction but with smaller, more manageable numbers. This simplification process makes calculations easier, improves understanding, and facilitates comparisons between different fractions. For example, while 40/900 might seem complex, simplifying it reveals a much clearer representation of its value.
Simplifying 40/900: A Step-by-Step Guide
The process of simplifying 40/900 involves finding the greatest common divisor (GCD) of the numerator (40) and the denominator (900). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
-
Finding the GCD: We can use several methods to find the GCD of 40 and 900. One common method is prime factorization. The prime factorization of 40 is 2³ x 5, and the prime factorization of 900 is 2² x 3² x 5². The common factors are 2² and 5. Therefore, the GCD is 2² x 5 = 20.
-
Dividing the Numerator and Denominator: Now, we divide both the numerator and the denominator by the GCD (20):
40 ÷ 20 = 2 900 ÷ 20 = 45
-
Simplified Fraction: The simplified fraction is therefore 2/45. This represents the same value as 40/900 but is much easier to work with.
Converting 40/900 to a Decimal: Understanding the Process
Converting a fraction to a decimal involves dividing the numerator by the denominator. Using the simplified fraction 2/45, we perform the division:
2 ÷ 45 ≈ 0.0444
The result is an approximate decimal value because the division results in a repeating decimal (0.0444...). We can round this to a specific number of decimal places depending on the required level of precision. For example, rounding to three decimal places gives us 0.044.
Representing 40/900 as a Percentage: Practical Applications
Converting a fraction to a percentage involves multiplying the decimal equivalent by 100. Using the decimal approximation 0.0444, we calculate the percentage:
0.0444 x 100 ≈ 4.44%
This percentage representation is particularly useful in various applications, such as expressing proportions, calculating discounts, or representing data in charts and graphs. For example, if 40 out of 900 students passed an exam, we can say that approximately 4.44% of the students passed.
Real-World Applications of 40/900 and its Simplified Form: Examples in Various Fields
The fraction 40/900, and its simplified form 2/45, has several practical applications across diverse fields:
-
Statistics and Probability: In statistical analysis, this fraction could represent the probability of a specific event occurring. For example, if 40 out of 900 trials resulted in a particular outcome, the probability of that outcome is 2/45 or approximately 4.44%.
-
Finance and Accounting: In financial calculations, 40/900 might represent a proportion of a total investment, a percentage of a debt, or a ratio of expenses to revenue. The simplified fraction makes these calculations much simpler.
-
Engineering and Construction: In engineering and construction projects, fractions are often used to represent ratios of materials, dimensions, or tolerances. Simplifying the fraction 40/900 improves the accuracy and efficiency of calculations.
-
Education and Assessment: As mentioned earlier, the fraction could represent the percentage of students who passed an exam, the proportion of correct answers on a test, or the success rate of a particular learning method.
-
Data Analysis and Representation: In data analysis, fractions can be used to represent proportions within datasets. The simplified fraction simplifies the visualization and interpretation of data.
Understanding the Concept of Ratio and Proportion: Expanding on the Fraction's Meaning
The fraction 40/900 can also be understood as a ratio, expressing a relationship between two quantities. It signifies that for every 900 units of the whole, there are 40 units of a specific part. This concept of ratio and proportion is fundamental in many mathematical and scientific applications. The simplified ratio, 2:45, communicates the same relationship in a more concise manner.
Further Mathematical Explorations: Extending the Concepts
Beyond simplification, decimal conversion, and percentage representation, the fraction 40/900 opens doors to more complex mathematical concepts. For instance:
-
Equivalent Fractions: Numerous fractions are equivalent to 40/900 and 2/45. These include 80/1800, 120/2700, and so on. Understanding equivalent fractions strengthens the understanding of fractional equivalence.
-
Fraction Operations: The fraction 40/900 can be used in various arithmetic operations, such as addition, subtraction, multiplication, and division with other fractions.
-
Algebraic Expressions: Fractions can be incorporated into algebraic expressions and equations, forming the basis for more advanced mathematical concepts.
Frequently Asked Questions (FAQs)
Q1: Is 2/45 the simplest form of 40/900?
A1: Yes, 2/45 is the simplest form of 40/900 because the greatest common divisor of 2 and 45 is 1. No further simplification is possible.
Q2: What are some other methods for finding the GCD of 40 and 900?
A2: Besides prime factorization, other methods for finding the GCD include the Euclidean algorithm and the least common multiple (LCM) method.
Q3: How can I convert 2/45 back to 40/900?
A3: To convert 2/45 back to 40/900, simply multiply both the numerator and the denominator by 20 (the GCD we initially found).
Q4: Why is simplifying fractions important?
A4: Simplifying fractions makes calculations easier, improves understanding, and facilitates comparisons between different fractions. It also presents the information in a clearer and more concise form.
Q5: Are there any limitations to using decimal approximations of fractions?
A5: Yes, using decimal approximations can lead to slight inaccuracies, especially when dealing with repeating decimals. The level of precision needed dictates the number of decimal places to use.
Conclusion: The Power of Understanding Simple Fractions
The seemingly simple fraction 40/900, when examined thoroughly, reveals a wealth of mathematical concepts and practical applications. By understanding the processes of simplification, decimal conversion, and percentage representation, we can effectively utilize this fraction in various contexts. This exploration not only reinforces basic arithmetic skills but also enhances understanding of more advanced mathematical principles, highlighting the importance of mastering fundamental concepts in mathematics. The ability to manipulate and interpret fractions is a crucial skill applicable across a vast range of disciplines and everyday situations.
Latest Posts
Latest Posts
-
0 75 X 3
Sep 11, 2025
-
127lbs To Kg
Sep 11, 2025
-
1000 Times 1000
Sep 11, 2025
-
52f To Celsius
Sep 11, 2025
-
22kg To Lbs
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 900 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.