0.75 X 3
stanleys
Sep 11, 2025 · 6 min read
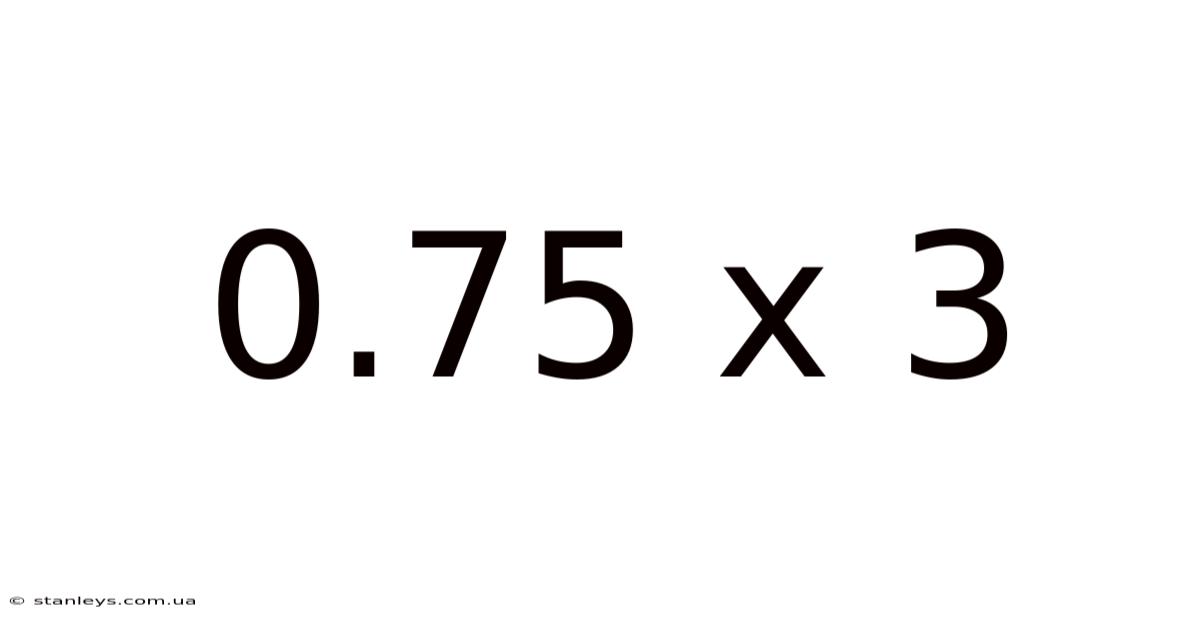
Table of Contents
Unveiling the Simplicity and Power of 0.75 x 3: A Deep Dive into Multiplication
This article explores the seemingly simple calculation of 0.75 multiplied by 3, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll examine various methods for solving this problem, discuss the importance of understanding decimal multiplication, and explore how this fundamental concept connects to more complex mathematical ideas. This guide is designed for learners of all levels, from elementary school students grasping the basics of multiplication to those seeking a deeper understanding of numerical operations. 0.75 x 3 might seem trivial at first glance, but its exploration unlocks a world of mathematical understanding.
Understanding Decimal Numbers: A Foundation for Multiplication
Before tackling the calculation itself, it's crucial to understand the nature of decimal numbers. Decimals represent fractions where the denominator is a power of 10 (e.g., 10, 100, 1000). The number 0.75, for instance, represents seventy-five hundredths, or 75/100. This fractional representation is key to understanding how decimal multiplication works. Understanding this fundamental concept allows us to approach more complex decimal multiplications with confidence. We can visualize 0.75 as a portion of a whole, which will be helpful in understanding the outcome of the multiplication.
Method 1: Direct Multiplication using the Standard Algorithm
The most straightforward method for solving 0.75 x 3 involves using the standard multiplication algorithm. This method involves multiplying each digit of 0.75 by 3, considering place value and carrying over when necessary.
- Multiply the hundredths place: 3 x 5 = 15. Write down '5' and carry-over '1'.
- Multiply the tenths place: 3 x 7 = 21. Add the carried-over '1' to get 22. Write down '22'.
- Determine the decimal point: Since 0.75 has two decimal places, the result will also have two decimal places.
Therefore, 0.75 x 3 = 2.25
Method 2: Fractional Conversion and Multiplication
Alternatively, we can convert the decimal 0.75 into a fraction and perform the multiplication using fractional arithmetic. This method provides a deeper understanding of the underlying mathematical operations.
- Convert 0.75 to a fraction: 0.75 is equivalent to 75/100.
- Simplify the fraction: 75/100 simplifies to 3/4 (by dividing both numerator and denominator by 25).
- Perform the multiplication: (3/4) x 3 = 9/4
- Convert back to a decimal: 9/4 can be converted to a decimal by performing long division (9 divided by 4), resulting in 2.25.
This method highlights the equivalence between decimals and fractions, providing a richer understanding of the mathematical operations involved. It's a powerful technique for understanding the relationship between different number systems.
Method 3: Distributive Property and Mental Math
For those comfortable with mental arithmetic, the distributive property provides a quick and efficient approach. We can break down 0.75 into 0.5 + 0.25 and then multiply each part by 3:
- Break down 0.75: 0.75 = 0.5 + 0.25
- Distribute the multiplication: (0.5 + 0.25) x 3 = (0.5 x 3) + (0.25 x 3)
- Multiply each part: 0.5 x 3 = 1.5 and 0.25 x 3 = 0.75
- Add the results: 1.5 + 0.75 = 2.25
This method showcases the versatility of the distributive property and emphasizes the power of mental calculation strategies. It's a valuable skill for quick estimations and problem-solving.
Visual Representation: Understanding the Multiplication Geometrically
We can visualize 0.75 x 3 geometrically. Imagine a square representing one unit (1). Divide the square into four equal parts. Three of these four parts represent 0.75 (or 3/4). Multiplying by 3 means we're taking three sets of these three-quarters. This results in nine out of four parts, which is equivalent to two whole squares (2) and one-quarter (0.25), totaling 2.25. This visual method helps in understanding the magnitude of the answer and reinforces the concept of multiplication as repeated addition.
Real-World Applications: Connecting Math to Everyday Life
The calculation 0.75 x 3 appears surprisingly often in real-world scenarios. A few examples include:
- Calculating Costs: If an item costs $0.75, and you buy three, the total cost is 0.75 x 3 = $2.25.
- Measuring Quantities: If you need 0.75 liters of a liquid for a recipe and you need to triple the recipe, you'll require 0.75 x 3 = 2.25 liters.
- Calculating Percentages: 0.75 represents 75%, so multiplying 0.75 by 3 gives you 225%, often encountered in financial calculations or percentage increases.
- Unit Conversions: This calculation might be part of a larger unit conversion problem, where you're converting from one unit to another involving fractions or decimals.
Expanding the Concept: Exploring More Complex Multiplications
Understanding 0.75 x 3 provides a strong foundation for tackling more complex multiplication problems involving decimals. The principles remain the same: understanding place values, fractional equivalents, and the ability to use different calculation methods. This fundamental knowledge lays the groundwork for operations with larger decimals, multiple decimal numbers, and even algebraic expressions involving decimal variables. Mastering this simple multiplication empowers you to approach more challenging mathematical problems with confidence.
Frequently Asked Questions (FAQs)
Q1: Why is it important to understand the different methods for solving 0.75 x 3?
A1: Understanding multiple methods fosters a deeper comprehension of the underlying mathematical principles. Each approach reveals a different facet of the problem, enhancing your overall understanding and problem-solving skills.
Q2: Can I use a calculator to solve 0.75 x 3?
A2: Yes, calculators provide a quick and efficient way to solve this calculation. However, understanding the underlying mathematical principles is crucial for developing a strong foundation in mathematics.
Q3: What happens if I multiply 0.75 by a larger number, such as 10 or 100?
A3: Multiplying by 10 simply moves the decimal point one place to the right (resulting in 7.5), and multiplying by 100 moves it two places to the right (resulting in 75). This is because multiplying by powers of 10 is equivalent to shifting the place value.
Q4: How does understanding 0.75 x 3 help in more advanced math topics?
A4: This basic calculation builds a foundation for more complex mathematical concepts. Understanding decimal multiplication is essential in algebra, calculus, and various fields of science and engineering.
Conclusion: The Significance of a Simple Calculation
The seemingly simple equation 0.75 x 3 provides a gateway to a deeper understanding of mathematical concepts. By exploring different methods of solving this problem, we've uncovered fundamental principles of decimal multiplication, fractional arithmetic, and the distributive property. This exploration not only provides the answer (2.25) but also strengthens our mathematical intuition and problem-solving abilities. The simplicity of this calculation belies its significance as a stepping stone towards mastering more complex mathematical operations and their real-world applications. Remember, even the simplest mathematical problems hold the key to unlocking a world of mathematical understanding and application.
Latest Posts
Latest Posts
-
70 Of 5
Sep 12, 2025
-
350lb To Kg
Sep 12, 2025
-
137lb In Kg
Sep 12, 2025
-
165 In Kg
Sep 12, 2025
-
18 39 X 5
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 0.75 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.