40 Of 260
stanleys
Sep 15, 2025 · 5 min read
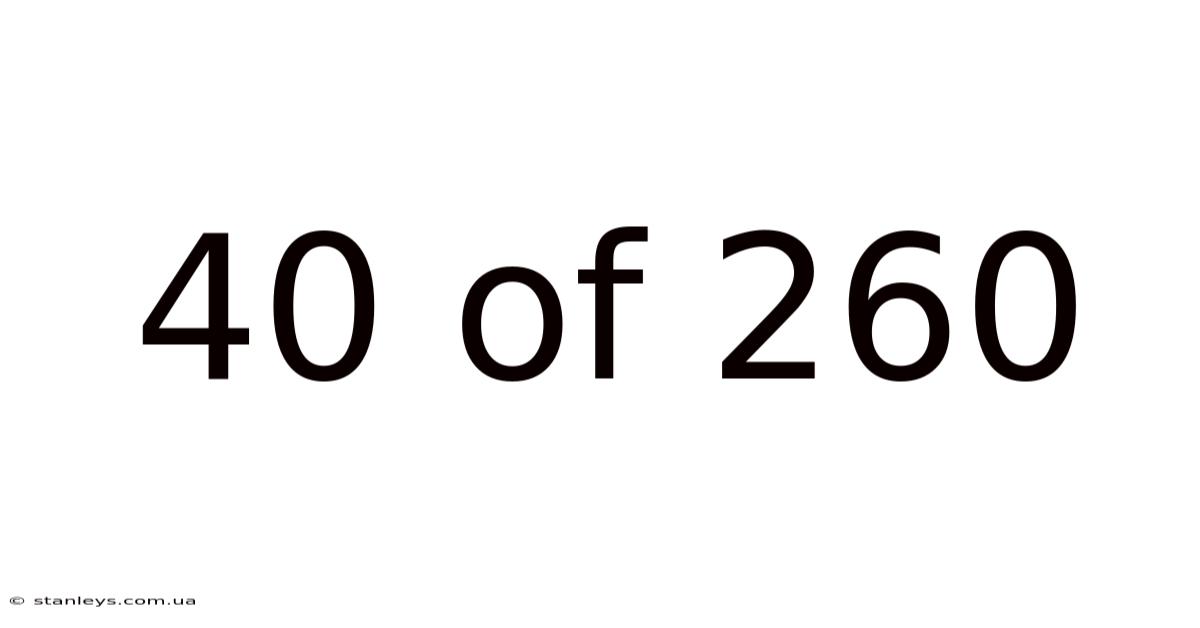
Table of Contents
Decoding 40 of 260: Understanding Fractions and Ratios in Context
This article delves into the meaning and implications of the fraction "40 of 260," exploring its mathematical representation, practical applications, and broader significance within the context of ratios and proportions. We'll move beyond a simple calculation to understand its conceptual underpinnings and how this seemingly simple fraction can be utilized in various real-world scenarios. This will involve looking at percentage calculations, simplifying fractions, and understanding the relationship between parts and wholes.
Understanding the Basics: Fractions and Ratios
Before diving into "40 of 260," let's establish a firm understanding of fundamental mathematical concepts. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we're considering, and the denominator indicates the total number of equal parts that make up the whole. For example, 1/2 represents one part out of two equal parts.
A ratio, on the other hand, compares the sizes of two or more quantities. It can be expressed as a fraction, using a colon (e.g., 1:2), or in words (e.g., "one to two"). Ratios are crucial for understanding proportions and scaling. Both fractions and ratios are interconnected; a fraction is essentially a specific type of ratio that compares a part to a whole.
Calculating 40 of 260: The Simple Approach
The phrase "40 of 260" directly translates into the fraction 40/260. This means 40 represents a part of a larger whole, which is 260. To understand the relationship between these two numbers, we can perform a simple calculation: We can express this fraction as a decimal by dividing the numerator by the denominator:
40 ÷ 260 = 0.1538 (approximately)
This means that 40 represents approximately 15.38% of 260.
Simplifying the Fraction: Finding the Lowest Terms
The fraction 40/260 isn't in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and denominator and divide both by it. The GCD of 40 and 260 is 20. Dividing both the numerator and the denominator by 20, we get:
40 ÷ 20 = 2 260 ÷ 20 = 13
Therefore, the simplified fraction is 2/13. This simplified fraction represents the same proportion as 40/260 but is easier to work with and understand. It tells us that 40 is 2 parts out of a total of 13 parts.
Understanding Proportions and Percentages
The fraction 40/260, or its simplified form 2/13, can also be expressed as a percentage. To do this, we convert the fraction to a decimal (as we did above) and then multiply by 100%:
0.1538 × 100% ≈ 15.38%
This means that 40 is approximately 15.38% of 260. This percentage representation offers a clear and concise way to understand the relative size of 40 compared to 260. Understanding percentages is crucial in various applications, from calculating discounts and taxes to analyzing data and understanding statistical information.
Real-World Applications of 40/260 (or 2/13)
The concept of "40 of 260" and its simplified form 2/13 finds applications in numerous real-world scenarios. Consider these examples:
- Test Scores: If a student answered 40 questions correctly out of a total of 260 questions on an exam, their score would be 15.38%.
- Survey Results: In a survey of 260 people, if 40 responded positively to a particular question, the positive response rate would be approximately 15.38%.
- Inventory Management: If a warehouse has 260 units of a particular product and 40 are sold, then 2/13 or approximately 15.38% of the inventory has been sold.
- Financial Analysis: If a company has a total revenue of 260 million dollars and a profit of 40 million dollars, the profit margin would be 15.38%.
Extending the Concept: Ratios and Proportions
The relationship between 40 and 260 can also be expressed as a ratio: 40:260. This ratio can be simplified to 2:13, indicating that for every 2 parts, there are 13 total parts. Understanding ratios is fundamental to solving proportion problems. A proportion is a statement that two ratios are equal. For example:
2/13 = x/100 (Solving for x, the equivalent percentage)
Illustrative Examples with Different Contexts:
Let's explore further examples demonstrating the flexibility of applying the 2/13 ratio:
-
Recipe Scaling: If a recipe calls for 2 cups of flour and 13 cups of water, you can scale it down to use 40 cups of flour and 260 cups of water (multiplying both by 20). The ratio remains the same, ensuring the recipe maintains its proportions.
-
Map Scales: Imagine a map with a scale of 2 cm representing 13 km. This is equivalent to our 2/13 ratio. You could use this to determine actual distances on the ground based on measurements on the map.
-
Probability: If an event has a probability of 2 out of 13 possible outcomes, that's exactly the same as the 40 out of 260 scenario.
Frequently Asked Questions (FAQ)
-
Q: How do I convert a fraction to a percentage? A: Divide the numerator by the denominator and then multiply the result by 100%.
-
Q: What is the difference between a fraction and a ratio? A: A fraction represents a part of a whole, while a ratio compares the sizes of two or more quantities. A fraction is a type of ratio.
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to understand and work with, and it allows for easier comparison with other fractions.
-
Q: Can I use a calculator for these calculations? A: Yes, calculators are very helpful, especially for more complex calculations or when dealing with large numbers.
Conclusion: Beyond the Numbers
This in-depth exploration of "40 of 260" illustrates that even seemingly simple mathematical expressions can hold significant meaning and application. By understanding the underlying concepts of fractions, ratios, proportions, and percentages, we can analyze and interpret data effectively in a wide range of situations. Remember, the ability to manipulate and interpret these concepts is crucial for success not only in mathematics but also in various other fields, such as science, finance, and engineering. The seemingly simple fraction 2/13 holds within it a wealth of mathematical power and real-world relevance. Mastering these fundamentals empowers you to approach quantitative problems with confidence and precision.
Latest Posts
Latest Posts
-
Minutes To Years
Sep 15, 2025
-
54 8kg To Stone
Sep 15, 2025
-
170kg In Lbs
Sep 15, 2025
-
64 1 3
Sep 15, 2025
-
24 X 6
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 260 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.