24 X 6
stanleys
Sep 15, 2025 · 6 min read
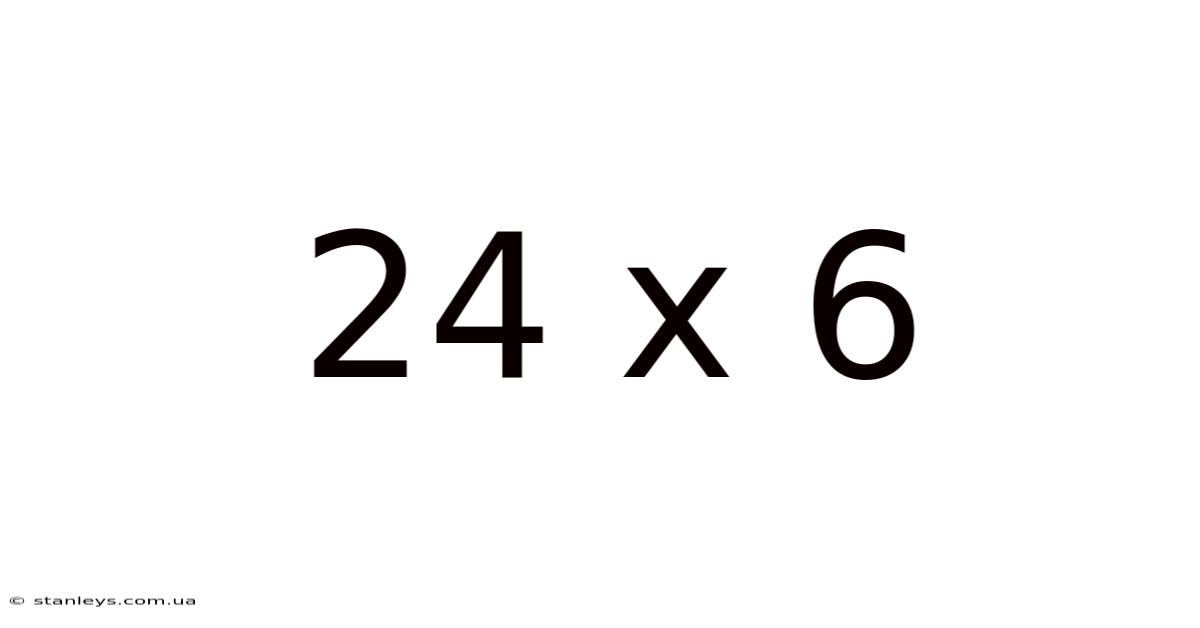
Table of Contents
Decoding 24 x 6: Exploring Multiplication, Area, and Real-World Applications
This article delves into the seemingly simple multiplication problem of 24 x 6, unraveling its mathematical significance and exploring its diverse applications in everyday life. We'll move beyond the basic calculation to understand the underlying principles, connecting this specific equation to broader concepts in mathematics and their practical relevance. This exploration is designed to be accessible to all, regardless of mathematical background, offering a deeper understanding of numbers and their role in our world.
Understanding the Basics: Multiplication and its Components
Before diving into the specifics of 24 x 6, let's refresh our understanding of multiplication. Multiplication is essentially repeated addition. When we say 24 x 6, we're essentially adding 24 to itself six times: 24 + 24 + 24 + 24 + 24 + 24. This fundamental concept forms the basis of all multiplication problems.
The numbers involved in multiplication have specific names. The number being multiplied (in this case, 24) is called the multiplicand. The number by which we multiply (6) is the multiplier. The result of the multiplication (which we will calculate shortly) is the product.
Calculating 24 x 6: Multiple Methods
There are several ways to calculate 24 x 6. The most common method taught in elementary school is the standard algorithm:
24
x 6
----
144
This involves multiplying the units digit (4) by the multiplier (6), resulting in 24. We write down the 4 and carry-over the 2. Next, we multiply the tens digit (2) by the multiplier (6), getting 12, and add the carry-over 2, resulting in 14. This gives us the final product: 144.
However, there are other, equally valid methods:
-
Distributive Property: We can break down 24 into smaller, easier-to-manage numbers. For instance, 24 can be expressed as 20 + 4. Using the distributive property, we have: (20 x 6) + (4 x 6) = 120 + 24 = 144. This method is particularly useful for mental calculations.
-
Repeated Addition: As mentioned earlier, we can simply add 24 six times: 24 + 24 + 24 + 24 + 24 + 24 = 144. While straightforward, this method becomes less efficient with larger numbers.
-
Using a Multiplication Table: A well-memorized multiplication table provides a quick way to find the product. Knowing that 6 x 4 = 24 and 6 x 20 = 120, we can easily add these two products together: 24 + 120 = 144.
Visualizing 24 x 6: The Area Model
Multiplication can be visualized geometrically using the area model. Imagine a rectangle with a length of 24 units and a width of 6 units. The area of this rectangle represents the product of 24 x 6. By dividing the rectangle into smaller, manageable sections (for example, a 20 x 6 rectangle and a 4 x 6 rectangle), we can visually represent the distributive property discussed earlier. The total area of these smaller rectangles will add up to the area of the larger 24 x 6 rectangle, thus providing a visual confirmation of the product, 144 square units.
Real-World Applications: Where Does 24 x 6 Show Up?
While 24 x 6 might seem like an abstract mathematical problem, it has numerous real-world applications:
-
Packaging and Inventory: Imagine a box containing 24 items, and you have 6 such boxes. To determine the total number of items, you would calculate 24 x 6 = 144. This is frequently used in warehousing, retail, and manufacturing.
-
Construction and Measurement: Calculating the area of a room measuring 24 feet by 6 feet requires the same multiplication: 24 x 6 = 144 square feet. This is essential for tasks like flooring, painting, or determining the amount of materials needed for a project.
-
Baking and Cooking: If a recipe calls for 24 grams of an ingredient per serving, and you need to make 6 servings, you'll need 24 x 6 = 144 grams of that ingredient. Accurate measurements are crucial in culinary arts.
-
Finance and Budgeting: Imagine you save $24 per week. After 6 weeks, you'll have saved $24 x 6 = $144. This is a simple example, but the principle applies to more complex financial calculations.
-
Travel and Distance: If you travel at an average speed of 24 miles per hour for 6 hours, the total distance covered will be 24 x 6 = 144 miles.
-
Gardening and Landscaping: If you plant 24 seedlings in each row and you have 6 rows, you have a total of 24 x 6 = 144 seedlings.
These examples highlight how seemingly simple mathematical operations like 24 x 6 are foundational to various aspects of our lives.
Extending the Concept: Factors, Multiples, and Prime Factorization
Understanding 24 x 6 also allows us to explore related mathematical concepts:
-
Factors: The factors of a number are the numbers that divide it evenly. The factors of 144 include 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, and 144. Understanding factors is crucial in simplifying fractions and solving algebraic equations.
-
Multiples: Multiples are the results of multiplying a number by other whole numbers. The multiples of 6 include 6, 12, 18, 24, 30, and so on. 144 is a multiple of both 6 and 24.
-
Prime Factorization: Every number can be expressed as a product of prime numbers (numbers divisible only by 1 and themselves). The prime factorization of 24 is 2 x 2 x 2 x 3, and the prime factorization of 6 is 2 x 3. Therefore, the prime factorization of 144 (24 x 6) is 2 x 2 x 2 x 2 x 2 x 3 x 3, or 2<sup>5</sup> x 3<sup>2</sup>. Prime factorization is fundamental in number theory and cryptography.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 24 x 6?
A: The easiest method depends on your personal preference and the tools available. The standard algorithm is generally taught first, but the distributive property (breaking 24 into 20 + 4) can be quicker for mental math. A multiplication table also offers a rapid solution.
Q: Are there any tricks to memorizing multiplication facts?
A: Yes! Flashcards, repetitive practice, and using visual aids like multiplication charts can significantly aid memorization. Understanding the patterns within multiplication tables can also make learning more efficient.
Q: Why is understanding multiplication important?
A: Multiplication is fundamental to many areas of mathematics and is essential for problem-solving in everyday life. From calculating costs to measuring areas to understanding proportions, multiplication skills are invaluable.
Q: Can I use a calculator for this type of problem?
A: Certainly! Calculators are useful tools for quickly obtaining answers, especially with larger numbers. However, understanding the underlying mathematical principles remains crucial.
Conclusion: Beyond the Numbers
This exploration of 24 x 6 has extended beyond a simple arithmetic problem. We've explored the fundamental concepts of multiplication, different calculation methods, the area model for visualization, real-world applications, and related mathematical concepts like factors, multiples, and prime factorization. The goal wasn't just to calculate 144, but to demonstrate the interconnectedness of mathematics and its pervasive influence on our daily lives. By understanding these underlying principles, we gain a deeper appreciation for the power and elegance of mathematics, empowering us to tackle more complex problems with confidence. The seemingly simple act of multiplying 24 by 6 opens up a world of mathematical possibilities and practical applications. So next time you encounter this seemingly simple calculation, remember the depth and breadth of understanding it can unlock.
Latest Posts
Latest Posts
-
1 25kg In Grams
Sep 15, 2025
-
Crossword Clue Sarcastic
Sep 15, 2025
-
Angry Crossword Clue
Sep 15, 2025
-
Art Of Cartooning
Sep 15, 2025
-
46 8kg In Stone
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 24 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.