40 Of 225
stanleys
Sep 17, 2025 · 5 min read
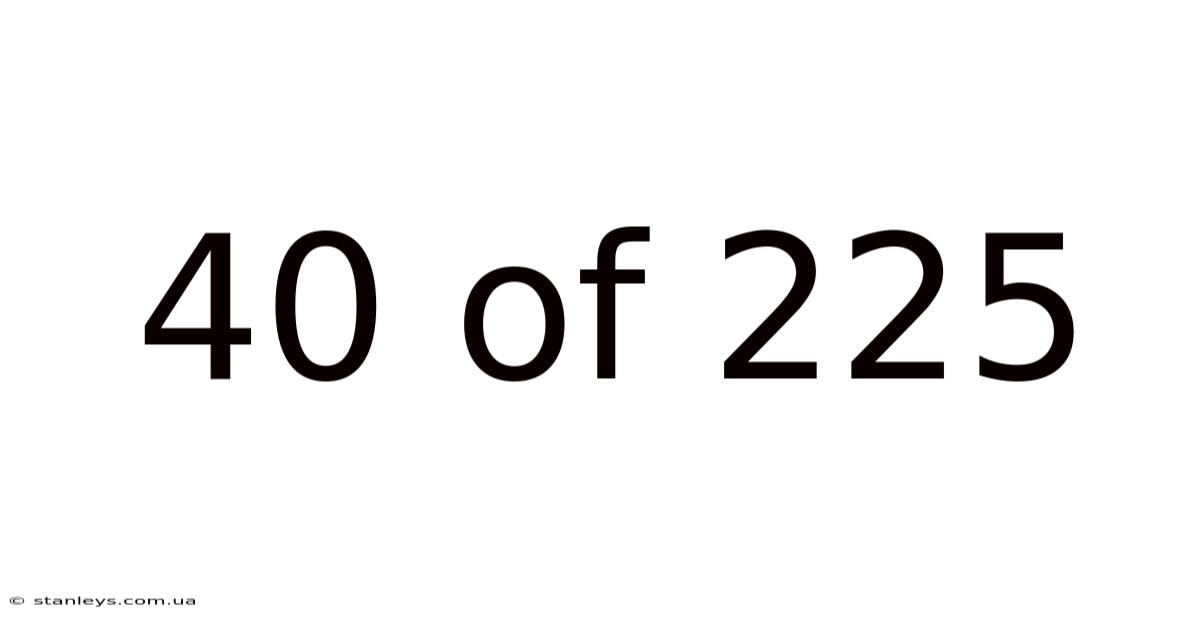
Table of Contents
Decoding the Fraction: Understanding 40/225 and its Implications
The seemingly simple fraction 40/225 might appear innocuous at first glance. However, understanding its underlying meaning and implications opens doors to a deeper appreciation of mathematical concepts and their real-world applications. This article delves into the intricacies of this fraction, exploring its simplification, decimal equivalent, percentage representation, and various contexts where such fractional representations become crucial. We will also examine the broader mathematical principles at play and offer practical examples to enhance comprehension.
I. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before delving deeper, the most fundamental step is simplifying 40/225 to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (40) and the denominator (225). The GCD is the largest number that divides both numbers without leaving a remainder.
One method to find the GCD is through prime factorization. Let's break down 40 and 225 into their prime factors:
- 40 = 2 x 2 x 2 x 5 = 2³ x 5
- 225 = 3 x 3 x 5 x 5 = 3² x 5²
By comparing the prime factorizations, we identify the common factors. In this case, the only common prime factor is 5. Therefore, the GCD of 40 and 225 is 5.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
40/5 = 8 225/5 = 45
Therefore, the simplified form of 40/225 is 8/45. This simplified fraction is easier to work with and represents the same proportion.
II. Converting to Decimal: Understanding the Decimal Equivalent
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. In this case, we divide 8 by 45:
8 ÷ 45 ≈ 0.17777...
This results in a repeating decimal, specifically 0.17777..., often written as 0.17̅7. The bar above the 7 indicates that the digit 7 repeats infinitely. Understanding repeating decimals is crucial in various mathematical applications, particularly in calculations involving percentages and ratios.
III. Representing as a Percentage: Expressing Proportion in Percentage Terms
To express the fraction as a percentage, we multiply the decimal equivalent by 100:
0.17̅7 x 100 ≈ 17.78%
This means that 40/225 represents approximately 17.78%. Percentage representation offers a readily understandable way to communicate proportions in various contexts, such as in statistics, finance, and everyday life.
IV. Real-World Applications and Contextual Understanding
The fraction 40/225, or its simplified form 8/45, can represent various real-world situations. Let’s consider a few examples:
-
Test Scores: Imagine a student answered 40 questions correctly out of a total of 225 questions on a test. Their score would be 40/225, or 8/45, which translates to approximately 17.78%. This percentage provides a clear and concise representation of the student’s performance.
-
Surveys and Statistics: If a survey of 225 people showed that 40 preferred a particular product, the fraction 40/225 (or 8/45) represents the proportion of people who favored that product. This proportion can then be expressed as a percentage (17.78%) for easier interpretation and comparison with other data.
-
Manufacturing and Quality Control: In a manufacturing process, if 40 out of 225 items produced are defective, the fraction 40/225 reflects the defect rate. Expressing this as a percentage helps determine the efficiency and quality of the production process.
-
Recipes and Proportions: Baking and cooking often involve fractional amounts of ingredients. If a recipe requires 225 grams of flour and only 40 grams of sugar, the fraction 40/225 illustrates the proportion of sugar relative to the total flour.
These examples highlight the versatility of fractional representations and their crucial role in quantifying real-world scenarios.
V. Further Mathematical Explorations: Extending the Understanding
Beyond simplification, decimal conversion, and percentage calculation, the fraction 40/225 opens doors to more advanced mathematical explorations:
-
Ratio and Proportion: The fraction represents a ratio of 40 to 225. Understanding ratios allows for solving proportions—finding an unknown value when other values are known in a proportional relationship. For example, if 40 items cost $x, and 225 items cost $100, we can use proportions to solve for x.
-
Fraction Operations: This fraction can be involved in addition, subtraction, multiplication, and division with other fractions, further enhancing skills in fractional arithmetic.
-
Algebraic Applications: Fractions often appear in algebraic equations and inequalities. Understanding fractional manipulations is essential for solving these types of mathematical problems.
-
Geometry and Measurement: Fractions play a key role in geometrical calculations involving areas, volumes, and measurements.
VI. Frequently Asked Questions (FAQ)
Q1: Are there other methods to find the GCD besides prime factorization?
A1: Yes, the Euclidean algorithm is another efficient method for finding the GCD of two numbers. This algorithm involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCD.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes calculations easier and provides a more concise representation of the proportion. It allows for easier comparison and interpretation of data.
Q3: What are the limitations of representing a repeating decimal?
A3: Repeating decimals can sometimes be approximated for practical purposes, but they represent an infinitely repeating sequence. In calculations requiring high precision, the repeating decimal nature needs to be considered carefully.
VII. Conclusion: The Significance of Fractional Understanding
The seemingly simple fraction 40/225 reveals a rich tapestry of mathematical concepts and real-world applications. Understanding its simplification, decimal equivalent, and percentage representation forms a cornerstone of basic mathematical literacy. Furthermore, exploring the fraction's broader implications within ratios, proportions, and other mathematical branches reinforces the interconnectedness of various mathematical ideas. Mastering fractional concepts is crucial for success in various academic disciplines and everyday problem-solving. By engaging with these concepts, we develop not only mathematical proficiency but also a deeper understanding of the world around us, expressed through quantifiable measures and proportions. The journey from a simple fraction to a comprehensive understanding of its implications underscores the power of mathematical exploration and its applicability in numerous fields. This journey encourages us to delve deeper into the intricacies of seemingly simple numerical expressions and to appreciate the broader mathematical context they represent.
Latest Posts
Latest Posts
-
3 5 Of 240
Sep 17, 2025
-
Magnesium Sulphide Formula
Sep 17, 2025
-
80 Of 55
Sep 17, 2025
-
Parasol Umbrella Black
Sep 17, 2025
-
27 X 9
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 225 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.