40 Of 220
stanleys
Sep 10, 2025 · 6 min read
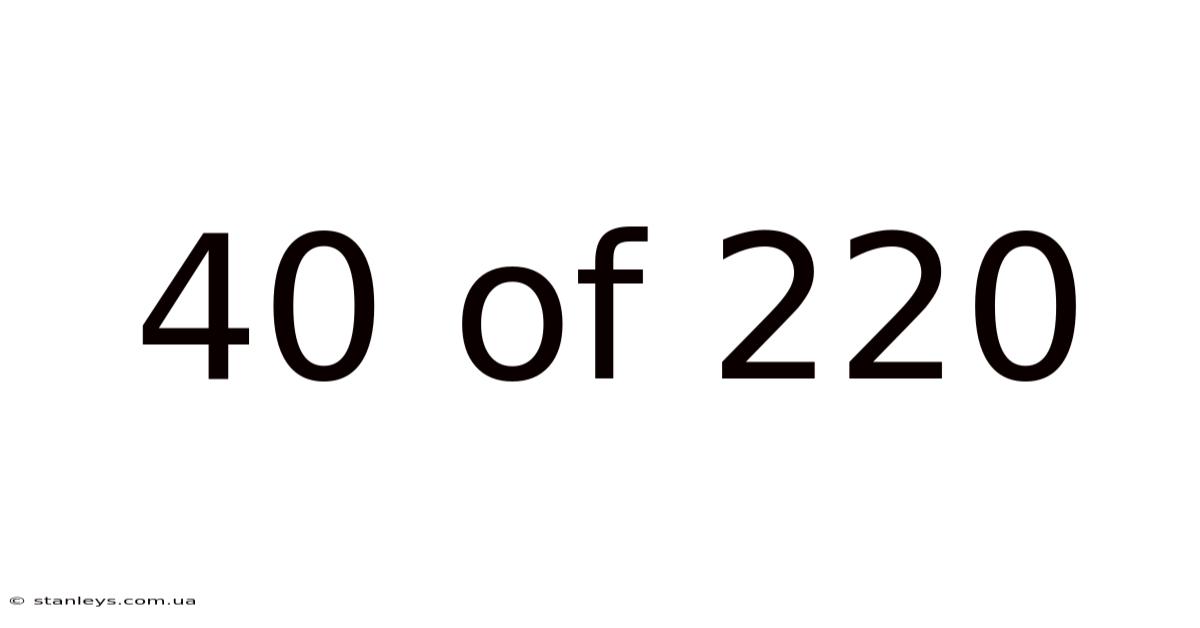
Table of Contents
Decoding 40 of 220: Understanding Ratios and Proportions in Everyday Life
Introduction:
The seemingly simple fraction "40 of 220" represents a fundamental concept in mathematics: ratios and proportions. Understanding this seemingly basic concept unlocks the ability to solve a wide array of problems, from calculating cooking ingredients to analyzing financial data and understanding statistical probabilities. This article will delve deep into the meaning of 40 out of 220, explore various methods to interpret and simplify it, and demonstrate its practical applications in everyday situations. We will cover the mathematical principles behind it, explore different ways to represent the ratio, and illustrate its relevance through real-world examples. By the end, you'll not only understand what 40 out of 220 means but also possess the tools to confidently tackle similar proportional problems.
What Does "40 of 220" Mean?
"40 of 220" simply means that there are 40 items or units out of a total of 220. It expresses a part-to-whole relationship. This ratio can be interpreted in various contexts, depending on the situation:
- Percentage: It represents a portion or percentage of the whole. We'll calculate this later.
- Fraction: It can be expressed as a fraction: 40/220.
- Probability: If we're dealing with a random selection, it could represent the probability of selecting one of the 40 items from the total 220.
- Proportion: It forms part of a larger proportional relationship; for example, if 40 out of 220 students passed an exam, we can use this ratio to predict the performance of a larger group.
Simplifying the Ratio: Finding the Simplest Form
The fraction 40/220 can be simplified by finding the greatest common divisor (GCD) of both the numerator (40) and the denominator (220). The GCD is the largest number that divides both numbers without leaving a remainder. In this case, the GCD of 40 and 220 is 20.
Dividing both the numerator and the denominator by 20, we get:
40 ÷ 20 = 2 220 ÷ 20 = 11
Therefore, the simplest form of the ratio 40/220 is 2/11. This simplified fraction retains the same proportional relationship as the original ratio but is easier to work with.
Expressing the Ratio as a Percentage
To express the ratio as a percentage, we first simplify the fraction (as shown above) to 2/11. Then, we convert the fraction to a decimal by dividing the numerator by the denominator:
2 ÷ 11 ≈ 0.1818
To convert this decimal to a percentage, we multiply by 100:
0.1818 × 100 ≈ 18.18%
Therefore, 40 out of 220 represents approximately 18.18%.
Real-World Applications: Examples of 40 of 220 in Different Contexts
The ratio 40 of 220, or its simplified form 2/11, can be applied to various scenarios:
-
Test Scores: If 40 out of 220 students passed a particular exam, the pass rate is 18.18%. This information is crucial for evaluating the exam's difficulty and the students' understanding of the subject matter. The school might use this data to adjust teaching methods or curriculum.
-
Manufacturing Quality Control: If a factory produces 220 items, and 40 are found to be defective, the defect rate is 18.18%. This helps identify areas for improvement in the manufacturing process to reduce defects and improve product quality.
-
Market Research: In a survey of 220 people, if 40 prefer a specific product, the market share for that product is approximately 18.18%. This helps companies understand consumer preferences and tailor their marketing strategies.
-
Sports Statistics: If a basketball player attempts 220 shots and makes 40, their shooting percentage is 18.18%. This is a crucial statistic for evaluating the player's performance.
-
Financial Analysis: If a portfolio of 220 stocks shows a gain in 40 of them, the success rate of the portfolio's investments is 18.18%. This information helps investors assess the performance of their investments and adjust their strategies accordingly.
Proportional Reasoning: Scaling Up and Down
The beauty of ratios lies in their ability to scale proportionally. Let's say a recipe calls for 40 grams of flour for every 220 grams of total ingredients. We can use the ratio to scale the recipe up or down:
-
Doubling the recipe: To double the recipe, we would multiply both the flour amount and the total ingredient amount by 2: 80 grams of flour and 440 grams of total ingredients.
-
Halving the recipe: To halve the recipe, we would multiply both amounts by 0.5: 20 grams of flour and 110 grams of total ingredients.
This proportional scaling maintains the same ratio (2/11) throughout.
Understanding Proportions with Cross-Multiplication
Proportions can be solved using cross-multiplication. Suppose we want to find the number of defective items in a batch of 550 items, given that the defect rate is the same as 40 out of 220. We can set up a proportion:
40/220 = x/550
Cross-multiplying gives us:
40 * 550 = 220 * x
22000 = 220x
x = 22000 / 220
x = 100
Therefore, we can expect approximately 100 defective items in a batch of 550 items, given the same defect rate.
Beyond the Basics: Advanced Applications
The concept of ratios and proportions extends far beyond simple calculations. It's integral to:
-
Statistics: Calculating probabilities, analyzing data distributions, and interpreting statistical significance.
-
Finance: Determining investment returns, calculating loan interest, and managing financial portfolios.
-
Engineering: Designing structures, calculating forces, and ensuring proper scaling in construction.
-
Chemistry: Determining chemical reaction ratios and stoichiometry.
Frequently Asked Questions (FAQ)
Q: What is the difference between a ratio and a proportion?
A: A ratio is a comparison of two quantities. A proportion is a statement that two ratios are equal. For example, 40/220 is a ratio. The statement 40/220 = 2/11 is a proportion.
Q: Can I use a calculator to simplify fractions?
A: Yes, most calculators have a function to simplify fractions. Alternatively, you can use online fraction calculators. However, understanding the manual process of finding the GCD is essential for a deeper grasp of the concept.
Q: How do I handle ratios with more than two numbers?
A: Ratios can involve more than two quantities. For instance, a ratio of 3:2:1 represents three quantities in a specific proportion. The principles of simplification and proportional reasoning still apply, but calculations might be more involved.
Q: What if I have a ratio with decimals?
A: You can often simplify ratios with decimals by multiplying both the numerator and denominator by a suitable power of 10 to eliminate the decimal points, turning the decimals into whole numbers. Then, you can proceed with simplification as usual.
Conclusion: Mastering Ratios and Proportions
Understanding ratios and proportions, as exemplified by the interpretation and application of "40 of 220," is a cornerstone of mathematical literacy. This concept extends beyond simple fraction calculations, influencing numerous aspects of daily life, from cooking and shopping to more complex fields like finance, science, and engineering. By grasping the fundamental principles discussed in this article, you've gained a powerful tool for analyzing data, solving problems, and making informed decisions in various contexts. Practice applying these concepts in real-world scenarios to solidify your understanding and build confidence in your mathematical abilities. The more you engage with proportional reasoning, the more intuitive and effortless it will become.
Latest Posts
Latest Posts
-
18 5 Of 982
Sep 10, 2025
-
92km To Miles
Sep 10, 2025
-
0 9 In Percentage
Sep 10, 2025
-
Singapore Olympic Games
Sep 10, 2025
-
1 5 Of 60
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.