1/5 Of 60
stanleys
Sep 10, 2025 · 6 min read
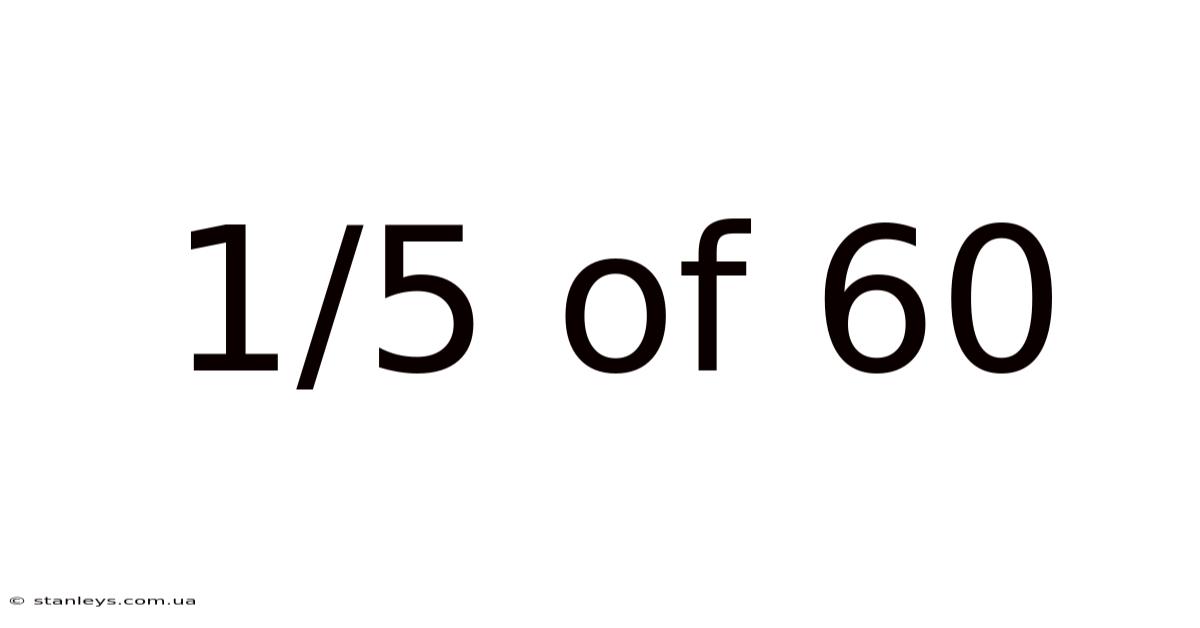
Table of Contents
Decoding 1/5 of 60: A Comprehensive Guide to Fractions and Their Applications
Understanding fractions is fundamental to mathematics and countless real-world applications. This article will delve into the seemingly simple calculation of "1/5 of 60," exploring the underlying principles of fractions, different methods of solving the problem, and expanding on the broader context of fractional arithmetic. We'll move beyond a simple answer to build a robust understanding of fractions, their significance, and how they apply to everyday situations. This guide is suitable for learners of all levels, from elementary school students to those looking to refresh their foundational math skills.
Understanding Fractions: The Building Blocks
Before tackling "1/5 of 60," let's establish a firm grasp of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator shows the total number of equal parts the whole is divided into.
For example, in the fraction 1/5, the numerator is 1, indicating we have one part, and the denominator is 5, indicating the whole is divided into five equal parts.
Key terms to remember:
- Numerator: The top number of a fraction.
- Denominator: The bottom number of a fraction.
- Proper fraction: A fraction where the numerator is smaller than the denominator (e.g., 1/5, 2/3).
- Improper fraction: A fraction where the numerator is larger than or equal to the denominator (e.g., 5/3, 4/4).
- Mixed number: A number consisting of a whole number and a proper fraction (e.g., 1 2/3).
Calculating 1/5 of 60: Multiple Approaches
Now, let's tackle the core problem: finding 1/5 of 60. There are several ways to solve this, each illustrating different aspects of fractional arithmetic.
Method 1: Direct Multiplication
The most straightforward approach is to interpret "of" as multiplication. Therefore, "1/5 of 60" translates to (1/5) * 60. To multiply a fraction by a whole number, we multiply the numerator by the whole number and keep the denominator the same:
(1/5) * 60 = (1 * 60) / 5 = 60/5
Now, we simplify the fraction by dividing the numerator by the denominator:
60/5 = 12
Therefore, 1/5 of 60 is 12.
Method 2: Division
Another effective approach involves dividing 60 into 5 equal parts. Since we're finding one-fifth, we divide the total (60) by the denominator (5):
60 ÷ 5 = 12
This method directly reflects the meaning of the fraction: dividing the whole into five equal parts and taking one of those parts.
Method 3: Using Decimals
We can convert the fraction 1/5 into its decimal equivalent. To do this, we divide the numerator (1) by the denominator (5):
1 ÷ 5 = 0.2
Now, we multiply the decimal equivalent (0.2) by 60:
0.2 * 60 = 12
This method highlights the interchangeability between fractions and decimals.
Method 4: Visual Representation
Imagine a group of 60 objects. To find 1/5 of 60, you would divide these 60 objects into 5 equal groups. Each group would contain:
60 ÷ 5 = 12 objects
This visual method is particularly helpful for beginners as it provides a concrete understanding of fractions.
Expanding on Fractional Concepts: Beyond the Basics
While calculating 1/5 of 60 is straightforward, understanding the broader context of fractions is crucial for mathematical proficiency. Let's explore some related concepts.
Equivalent Fractions: Different fractions can represent the same value. For example, 1/5, 2/10, and 3/15 are all equivalent fractions. They all represent the same portion of a whole. Simplifying fractions involves finding the equivalent fraction with the smallest numerator and denominator. In our example, 60/5 simplifies to 12/1, or simply 12.
Adding and Subtracting Fractions: To add or subtract fractions, they must have the same denominator (a common denominator). If they don't, we need to find equivalent fractions with a common denominator before performing the operation.
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
Real-World Applications of Fractions
Fractions are not just abstract mathematical concepts; they are integral to numerous aspects of daily life.
- Cooking and Baking: Recipes often use fractions to specify ingredient quantities (e.g., 1/2 cup of flour, 2/3 cup of sugar).
- Measurement: Measuring tools like rulers and measuring cups are marked with fractions (e.g., inches, centimeters, milliliters).
- Finance: Fractions are used to represent percentages, interest rates, and proportions of investments.
- Data Analysis: Fractions and their decimal equivalents are fundamental in representing and interpreting data, percentages, and probabilities.
- Geometry: Fractions are essential in calculating areas, volumes, and proportions in geometric figures.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 1/5?
A1: 1/5 is already in its simplest form. The numerator (1) and the denominator (5) share no common factors other than 1.
Q2: How do I find a fraction of a number without a calculator?
A2: You can use the methods described above: direct multiplication, division, or a combination of both. The key is to understand the underlying meaning of the fraction and how it relates to the whole number.
Q3: Can I use a calculator to solve 1/5 of 60?
A3: Yes, you can. Simply enter (1/5) * 60 into a calculator to obtain the result, 12.
Q4: What if I need to find more than 1/5 of 60, say 3/5 of 60?
A4: You would follow the same principles. (3/5) * 60 = (3 * 60) / 5 = 180 / 5 = 36. Alternatively, you could find 1/5 of 60 (which is 12) and then multiply by 3: 12 * 3 = 36.
Q5: Are there any online resources or tools that can help me practice fractions?
A5: Numerous websites and educational apps provide interactive exercises and tutorials on fractions, enabling you to practice at your own pace.
Conclusion: Mastering Fractions for a Brighter Future
This article has explored the calculation of "1/5 of 60" in detail, examining different approaches and broadening the discussion to cover essential concepts within fractional arithmetic. Mastering fractions is not merely about memorizing formulas; it's about developing a deep understanding of their meaning and their wide-ranging applicability. By understanding these fundamental concepts, you'll be better equipped to tackle more complex mathematical challenges and solve real-world problems that involve fractions. So, continue to practice, explore, and build your confidence in handling fractions – a skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
Spanish For Come
Sep 10, 2025
-
225lb To Kg
Sep 10, 2025
-
Centimeters To Micrometers
Sep 10, 2025
-
12x X 2
Sep 10, 2025
-
113 4kg In Stone
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1/5 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.