4 X X2
stanleys
Sep 14, 2025 · 5 min read
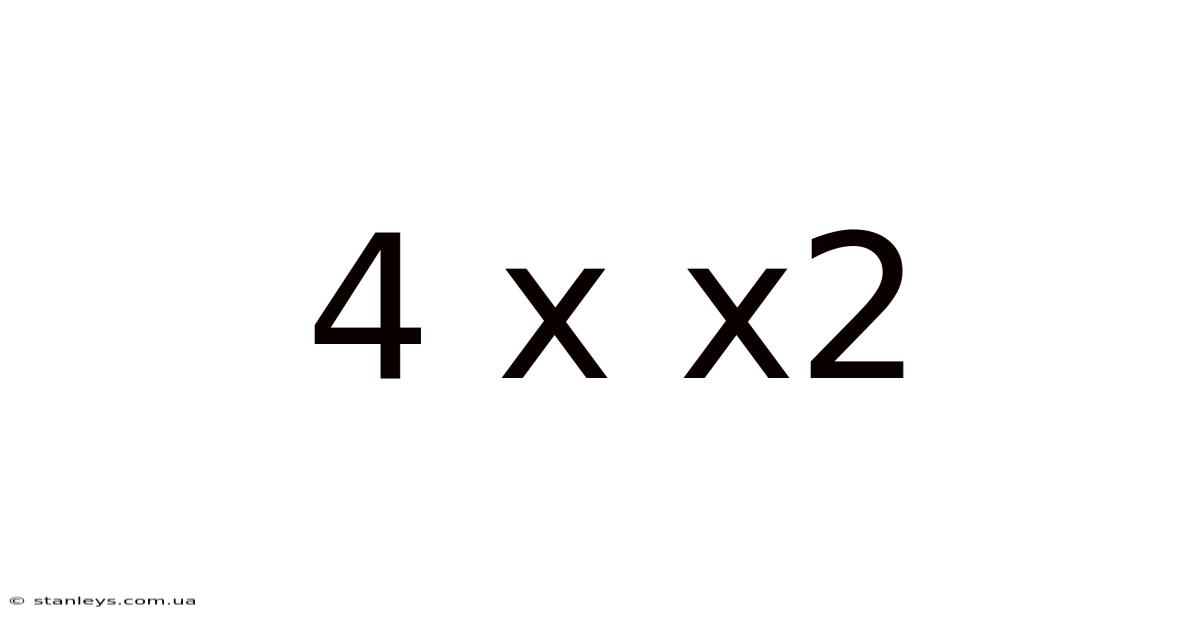
Table of Contents
Decoding 4 x x²: Unveiling the Secrets of Quadratic Expressions and Beyond
Understanding algebraic expressions, particularly those involving exponents, is fundamental to mastering mathematics. This article delves into the intricacies of the expression "4 x x²," breaking down its components, exploring its applications, and expanding its understanding to encompass broader mathematical concepts. We will explore its simplification, its graphical representation, and how it relates to higher-level mathematical ideas. This comprehensive guide is designed for students of all levels, from those just beginning their algebra journey to those seeking a deeper understanding of quadratic equations and beyond.
Introduction: Understanding the Building Blocks
The expression "4 x x²" is a seemingly simple algebraic statement, yet it encapsulates several key concepts. Let's break it down:
- 4: This is a constant, a numerical value that doesn't change.
- x: This is a variable, representing an unknown quantity. It can take on any numerical value.
- x²: This represents "x squared," or x multiplied by itself (x * x). This is an example of an exponent, indicating repeated multiplication.
Therefore, "4 x x²" signifies 4 multiplied by x multiplied by x². Understanding these fundamental building blocks is crucial before we proceed to simplification and broader applications.
Simplifying the Expression: Combining Like Terms
The expression can be simplified using the rules of exponents and multiplication. Remember that when multiplying terms with the same base (in this case, 'x'), we add their exponents. Even though it's not explicitly written, the 'x' has an exponent of 1 (x¹).
Therefore:
4 x x² = 4 x (x¹ x x²) = 4 x x⁽¹⁺²⁾ = 4x³
Thus, the simplified form of "4 x x²" is 4x³, representing four times x cubed. This simplified form makes further calculations and analysis much easier.
Graphical Representation: Visualizing the Function
The simplified expression, 4x³, represents a cubic function. Cubic functions are characterized by their S-shaped curves. To visualize this, we can plot points on a coordinate plane. By substituting different values for 'x', we can calculate corresponding values for 'y' (where y = 4x³). This creates a set of coordinates that can be plotted to generate the graph.
For instance:
- If x = 0, y = 4(0)³ = 0
- If x = 1, y = 4(1)³ = 4
- If x = 2, y = 4(2)³ = 32
- If x = -1, y = 4(-1)³ = -4
- If x = -2, y = 4(-2)³ = -32
Plotting these points and connecting them smoothly will reveal the characteristic S-shape of a cubic function. This visual representation offers valuable insights into the behavior of the function, including its increasing or decreasing nature and its intercepts.
Applications in Real-World Scenarios: Beyond the Classroom
The principles demonstrated by the expression 4x³ extend far beyond the confines of a textbook. Cubic functions, and their underlying algebraic principles, find applications in numerous real-world scenarios, including:
-
Volume Calculations: The volume of a cube is given by the formula side³. If the side length is represented by 'x', and we have four such cubes, the total volume would be 4x³. This illustrates a direct application of the expression in geometrical contexts.
-
Physics and Engineering: Many physical phenomena, such as the relationship between velocity, acceleration, and time, can be modeled using cubic functions. For instance, the distance traveled by an object under constant acceleration can be represented by a cubic equation.
-
Economics and Finance: Cubic functions can be used to model various economic phenomena, such as the relationship between production cost and output. In finance, they can be employed in the modeling of complex investment strategies.
Expanding the Understanding: Connecting to Broader Concepts
The expression "4 x x²" and its simplified form, 4x³, serve as a springboard to understanding more complex mathematical concepts:
-
Polynomials: The expression 4x³ is a polynomial, specifically a monomial (a polynomial with one term). Understanding polynomials is crucial for mastering algebra and calculus.
-
Derivatives and Integrals (Calculus): In calculus, we can find the derivative and integral of 4x³. The derivative represents the instantaneous rate of change of the function, while the integral represents the area under the curve. These concepts are fundamental to advanced mathematical analysis.
-
Series and Sequences: Understanding how to manipulate and simplify expressions like 4x³ is essential for working with series and sequences, which are used extensively in advanced mathematics and computer science.
Frequently Asked Questions (FAQ)
-
What happens if x is a negative number? If x is negative, the result of 4x³ will also be negative. This is because a negative number raised to an odd power (like ³) remains negative.
-
Can we solve for x? No, we cannot solve for 'x' without additional information. The expression 4x³ is an equation only if it's set equal to another value (e.g., 4x³ = 64). Solving such an equation requires additional algebraic techniques.
-
What is the difference between 4x³ and (4x)³? There's a significant difference. 4x³ means 4 multiplied by x³, while (4x)³ means (4x) multiplied by itself three times, resulting in 64x³.
-
How can I learn more about cubic functions? Further exploration into the characteristics and applications of cubic functions can be achieved through various resources, including textbooks, online tutorials, and educational websites dedicated to mathematics and algebra.
Conclusion: Mastering the Fundamentals, Reaching for the Future
Understanding the expression "4 x x²," its simplification to 4x³, and its connections to broader mathematical concepts is a crucial step in building a strong foundation in mathematics. This seemingly simple expression unveils a wealth of knowledge, showcasing the power of algebra and its applications in diverse fields. By mastering the fundamentals, students can confidently approach more complex mathematical challenges and unlock their potential for future academic and professional success. The journey from a simple algebraic expression to understanding cubic functions and beyond is a testament to the beauty and interconnectedness of mathematical concepts. Embrace the challenge, explore the possibilities, and witness your mathematical understanding blossom.
Latest Posts
Latest Posts
-
21lb In Kg
Sep 14, 2025
-
25 Of 19
Sep 14, 2025
-
Duchess Of Newcastle
Sep 14, 2025
-
Milligram To Kg
Sep 14, 2025
-
0 03 As Fraction
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4 X X2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.