25 Of 19
stanleys
Sep 14, 2025 · 6 min read
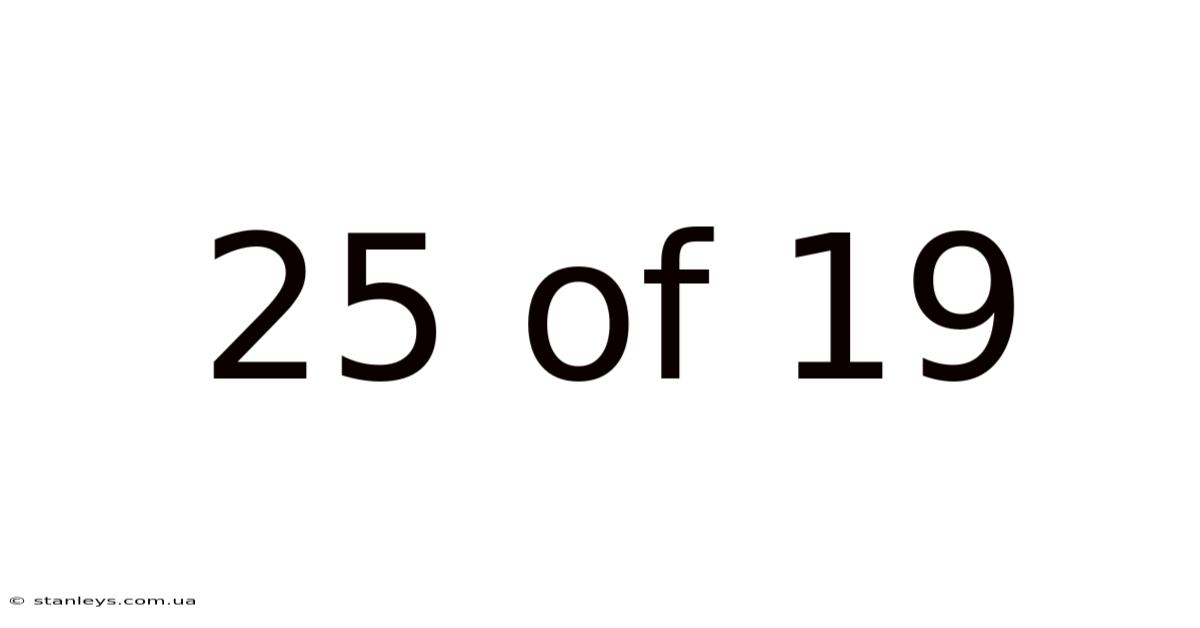
Table of Contents
Decoding the Enigma: Understanding the Fraction 25/19
The seemingly simple fraction 25/19 holds a wealth of mathematical concepts within its concise form. Understanding this fraction goes beyond simply knowing its decimal equivalent; it's about grasping the underlying principles of fractions, decimals, percentages, and their applications in everyday life. This article delves into the intricacies of 25/19, exploring its representation in various forms, its mathematical properties, and its practical implications. We'll unpack this fraction step-by-step, making it accessible and engaging for readers of all mathematical backgrounds.
I. Introduction: What is 25/19?
The fraction 25/19 represents a ratio or a part of a whole. The number 25 is the numerator, indicating the number of parts we have, while 19 is the denominator, indicating the total number of equal parts that make up the whole. Because the numerator is larger than the denominator, 25/19 is an improper fraction, meaning it represents a value greater than one. This contrasts with a proper fraction, where the numerator is smaller than the denominator.
II. Converting 25/19 to Different Forms
Understanding 25/19 fully requires exploring its representations in different mathematical forms.
A. Decimal Representation:
To convert 25/19 to a decimal, we perform long division: 25 divided by 19. This yields approximately 1.315789. This decimal is a non-terminating, repeating decimal, meaning it continues infinitely without a repeating pattern. This is a common characteristic of fractions where the denominator has prime factors other than 2 and 5.
B. Mixed Number Representation:
An improper fraction like 25/19 can be converted into a mixed number, which combines a whole number and a proper fraction. To do this, we divide the numerator (25) by the denominator (19). The quotient (1) becomes the whole number part, and the remainder (6) becomes the numerator of the fractional part, keeping the same denominator (19). Thus, 25/19 as a mixed number is 1 6/19.
C. Percentage Representation:
To express 25/19 as a percentage, we multiply the decimal representation (approximately 1.315789) by 100%. This gives us approximately 131.58%. This indicates that 25/19 represents 131.58% of a whole.
III. Mathematical Operations with 25/19
Understanding 25/19 involves exploring how it interacts within various mathematical operations.
A. Addition and Subtraction:
Adding or subtracting fractions requires a common denominator. To add or subtract 25/19 with another fraction, you'll first need to find a common denominator and then perform the operation on the numerators. For example, adding 25/19 to 1/2 would require finding a common denominator (38), converting both fractions, and then adding the numerators.
B. Multiplication and Division:
Multiplication of fractions is straightforward: multiply the numerators together and the denominators together. For example, multiplying 25/19 by 2/3 would result in (252)/(193) = 50/57.
Dividing fractions involves inverting the second fraction (the divisor) and then multiplying. Dividing 25/19 by 3/4 would be equivalent to multiplying 25/19 by 4/3, resulting in (254)/(193) = 100/57.
IV. Practical Applications of 25/19
While seemingly abstract, fractions like 25/19 find practical applications in various real-world scenarios.
-
Ratio and Proportion: The fraction could represent a ratio, such as the ratio of apples to oranges in a fruit basket. If there are 25 apples and 19 oranges, the ratio is 25/19.
-
Measurement and Conversion: Imagine a scenario involving measurements where you need to convert units. If a recipe calls for 25 units of ingredient A and 19 units of ingredient B, the ratio is 25/19.
-
Financial Calculations: In finance, ratios like 25/19 could represent the relationship between assets and liabilities, or between revenue and expenses.
V. Explaining the Concept to a Beginner
Imagine you have 25 delicious cookies, and you want to share them equally among 19 friends. Each friend would receive a little more than one cookie (25/19). This is a simple way to visually represent the fraction and its value. Breaking down complex concepts into relatable scenarios makes learning easier.
VI. Understanding the Significance of Improper Fractions
The fact that 25/19 is an improper fraction is significant because it indicates a quantity greater than one. This understanding is crucial for solving problems involving quantities exceeding a whole unit. Improper fractions are often easier to manipulate in calculations, especially when performing multiplication or division.
VII. Common Mistakes and How to Avoid Them
A common mistake is misinterpreting the meaning of the numerator and denominator. Always remember that the numerator represents the part and the denominator represents the whole. Another frequent error is incorrectly converting improper fractions to mixed numbers or decimals. Always double-check your calculations to prevent errors.
VIII. Advanced Concepts Related to 25/19
Exploring the prime factorization of the numerator and denominator provides insights into the fraction's properties. The prime factorization of 25 is 5 x 5, and the prime factorization of 19 is simply 19 (as 19 is a prime number). This prime factorization can help in simplifying fractions and understanding common factors. Furthermore, understanding continued fractions, a way of expressing a number as a sum of unit fractions, could provide alternative representations of 25/19.
IX. Frequently Asked Questions (FAQ)
Q1: How do I simplify 25/19?
A1: The fraction 25/19 is already in its simplest form because 25 and 19 do not share any common factors other than 1.
Q2: Can 25/19 be expressed as a terminating decimal?
A2: No, 25/19 cannot be expressed as a terminating decimal because the denominator (19) contains a prime factor (19) other than 2 or 5.
Q3: What is the reciprocal of 25/19?
A3: The reciprocal of 25/19 is 19/25. The reciprocal is found by switching the numerator and denominator.
Q4: How do I convert 25/19 to a percentage?
A4: Divide 25 by 19 (approximately 1.3158) and then multiply by 100 to get approximately 131.58%.
X. Conclusion: Mastering the Fundamentals
Understanding a fraction like 25/19 is about more than just finding its decimal equivalent. It involves grasping the underlying principles of fractions, decimals, and percentages, and how these concepts interconnect. By exploring its different representations, mathematical operations, and practical applications, we build a stronger foundation in mathematics. This holistic approach to understanding seemingly simple concepts like 25/19 empowers learners to tackle more complex mathematical challenges with confidence and competence. The journey of understanding 25/19 serves as a microcosm of the broader mathematical landscape, demonstrating the power of breaking down complex concepts into manageable, understandable components. This approach allows for deeper understanding and appreciation of the interconnectedness of mathematical ideas.
Latest Posts
Latest Posts
-
800g In Kg
Sep 14, 2025
-
52kg To Stone
Sep 14, 2025
-
Poems About Praise
Sep 14, 2025
-
2 7kg To Lbs
Sep 14, 2025
-
8 Of 300
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 19 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.