35 Of 250
stanleys
Sep 17, 2025 · 5 min read
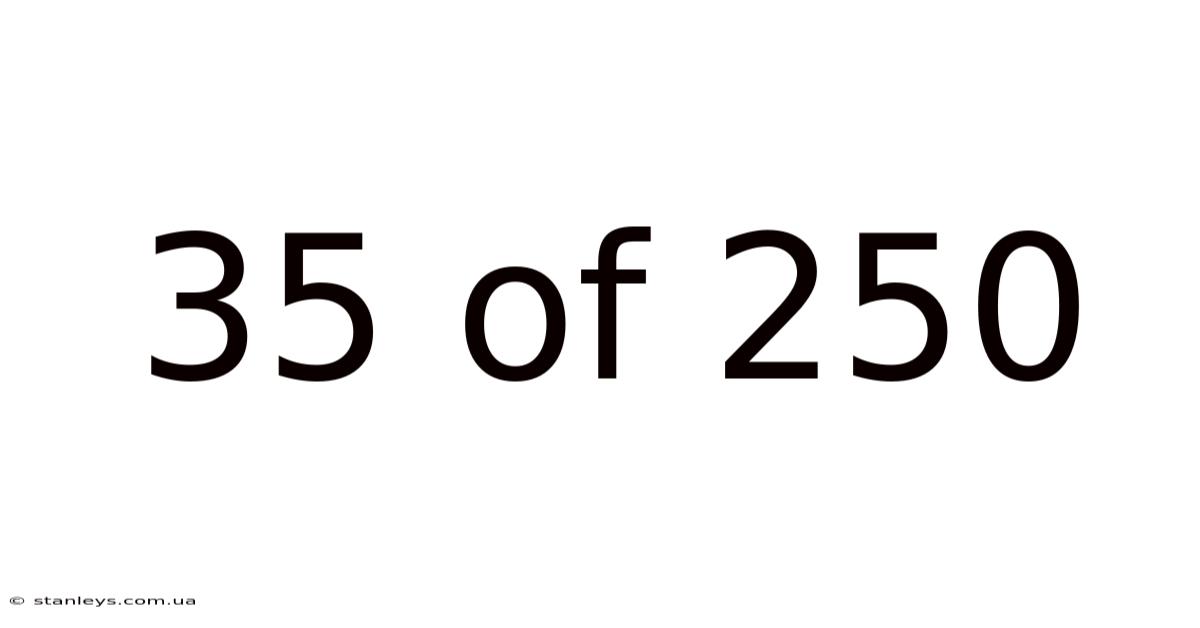
Table of Contents
Understanding the Significance of "35 of 250": A Deep Dive into Proportions, Percentages, and Practical Applications
This article explores the meaning and implications of the statement "35 of 250," focusing on its representation as a fraction, percentage, and its application in various real-world scenarios. We'll delve into the mathematical calculations, explore the importance of understanding proportions, and demonstrate how this seemingly simple concept plays a crucial role in data analysis, decision-making, and everyday life. Understanding ratios and proportions is a fundamental skill with broad applications across numerous fields.
Introduction: Deconstructing "35 of 250"
The phrase "35 of 250" represents a ratio or proportion. It indicates that 35 items represent a portion of a larger whole consisting of 250 items. This simple statement can be interpreted in several ways, offering valuable insights depending on the context. We will unpack its significance through mathematical calculations, real-world examples, and practical applications.
Expressing "35 of 250" Mathematically
The core of understanding "35 of 250" lies in its mathematical representation. We can express this ratio in several forms:
-
Fraction: The most straightforward representation is as a fraction: 35/250. This fraction signifies 35 parts out of a total of 250 parts.
-
Simplified Fraction: We can simplify this fraction by finding the greatest common divisor (GCD) of 35 and 250, which is 5. Dividing both the numerator and the denominator by 5, we get the simplified fraction 7/50. This simplified form makes it easier to grasp the proportion.
-
Decimal: Converting the fraction to a decimal involves dividing the numerator (35) by the denominator (250). This results in 0.14.
-
Percentage: To express the ratio as a percentage, we multiply the decimal value (0.14) by 100. Therefore, "35 of 250" represents 14%. This percentage clearly illustrates the proportion of 35 relative to 250.
Practical Applications and Real-World Scenarios
The concept of "35 of 250" has broad applications across various fields. Let's explore some examples:
-
Surveys and Statistics: Imagine a survey conducted on 250 individuals, where 35 responded positively to a particular question. The 14% positive response rate provides valuable insights into public opinion. This data can be used to make informed decisions, plan marketing strategies, or understand consumer preferences.
-
Quality Control: In manufacturing, if 250 products are inspected, and 35 are found to be defective, the 14% defect rate highlights the need for improvements in the production process. This data is crucial for maintaining quality standards and minimizing customer complaints.
-
Financial Analysis: In investment, if 35 out of 250 stocks in a portfolio perform well, it indicates a 14% success rate. This information is crucial for evaluating investment strategies and making informed decisions about future investments.
-
Academic Performance: If a student answers 35 questions correctly out of a total of 250 questions on an exam, their score is 14%. This percentage provides an accurate measure of their understanding of the subject matter.
-
Healthcare: In a clinical trial involving 250 patients, if 35 experience a positive outcome after a certain treatment, the 14% success rate is a key metric for evaluating the treatment's efficacy.
-
Environmental Science: If 35 out of 250 trees in a forest are affected by a disease, the 14% infection rate can help scientists understand the spread of the disease and develop mitigation strategies.
-
Sports Statistics: In a basketball game, if a player makes 35 shots out of 250 attempts, their shooting percentage is 14%. This metric provides insights into the player's shooting accuracy.
These examples demonstrate the versatility of understanding proportions. The ability to convert ratios into fractions, decimals, and percentages allows for clear communication and effective data interpretation.
Understanding Proportions: A Deeper Dive
Understanding proportions is fundamental to mathematics and essential for comprehending the relationship between parts and the whole. It involves comparing two ratios to determine if they are equivalent. A proportion is an equation stating that two ratios are equal. For instance, the proportion 35/250 = 7/50 signifies that these two ratios represent the same proportion. This understanding is crucial for:
-
Scaling: Proportions allow us to scale up or down quantities while maintaining the same ratio. For example, if a recipe calls for 7 parts flour to 50 parts water, we can easily scale it up to use 35 parts flour and 250 parts water, maintaining the original ratio.
-
Problem Solving: Proportions provide a systematic approach to solving many real-world problems, particularly those involving ratios, percentages, and scaling.
-
Data Analysis: Proportions are fundamental to analyzing data and extracting meaningful insights from statistical information.
Beyond the Numbers: Context is King
While the mathematical calculations are crucial, understanding the context in which "35 of 250" is used is equally important. The significance of 14% varies drastically depending on the situation. A 14% defect rate in manufacturing might be unacceptable, while a 14% success rate in a complex medical procedure could be considered quite significant. Contextual understanding determines the interpretation and implications of the ratio.
Frequently Asked Questions (FAQ)
-
How do I calculate the percentage from a fraction? To calculate a percentage from a fraction, divide the numerator by the denominator and then multiply the result by 100. For example, 35/250 = 0.14 * 100 = 14%.
-
What if I have a different ratio? How can I apply these principles? The principles discussed here apply to any ratio. Simply replace 35 and 250 with your numbers and follow the same calculation methods to express the ratio as a fraction, decimal, and percentage.
-
Why is understanding proportions important? Understanding proportions is crucial for various applications in mathematics, science, finance, and everyday life. It allows for accurate data interpretation, informed decision-making, and effective problem-solving.
-
Are there any online tools to calculate proportions? Yes, many online calculators and software programs can help with these calculations. However, understanding the underlying principles is essential for effective problem-solving and data interpretation.
Conclusion: The Power of Proportions
"35 of 250," while seemingly a simple statement, represents a powerful concept with wide-ranging applications. By understanding how to express this ratio as a fraction, decimal, and percentage, we can unlock valuable insights and make informed decisions across numerous fields. The ability to interpret and utilize proportions is a fundamental skill that empowers us to analyze data effectively, solve problems systematically, and navigate a complex world with greater understanding and confidence. Remember that while the numbers are important, the context in which they are applied dictates their ultimate meaning and significance. Mastering the art of understanding and applying proportions will undoubtedly enhance your analytical and problem-solving abilities.
Latest Posts
Latest Posts
-
180grams To Oz
Sep 17, 2025
-
28 Times 5
Sep 17, 2025
-
24 Of 75
Sep 17, 2025
-
3 Dl Ml
Sep 17, 2025
-
Hard To Beat
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.