35 Of 120
stanleys
Sep 12, 2025 · 6 min read
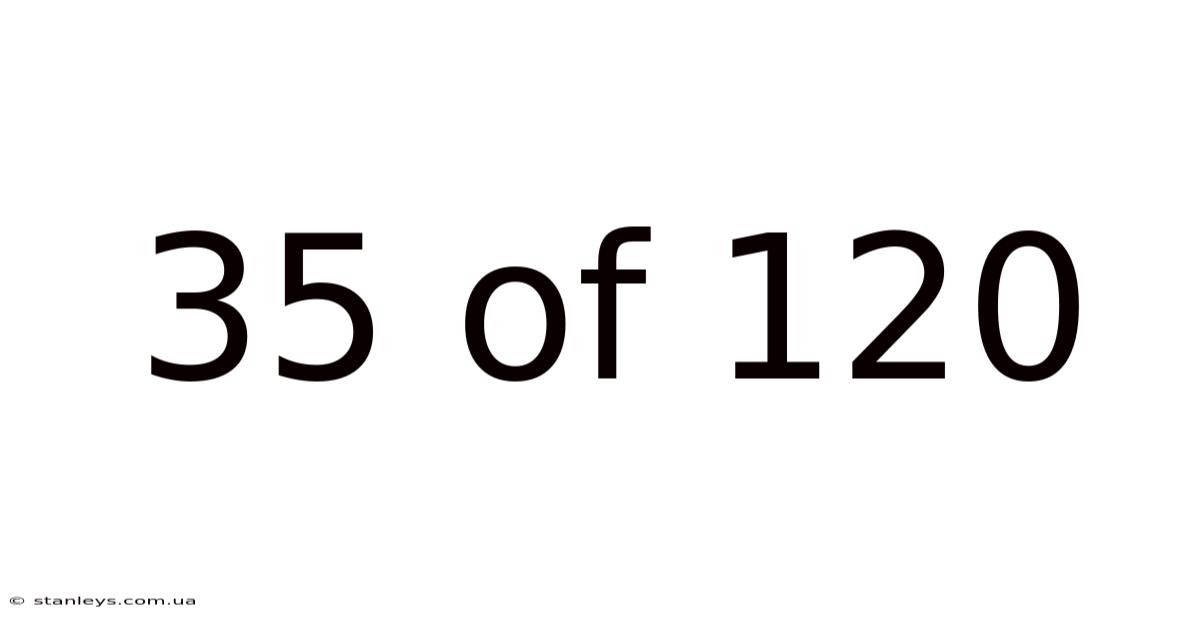
Table of Contents
Decoding the Fraction: 35 out of 120 – Understanding Percentages, Ratios, and Applications
Understanding fractions is a fundamental skill in mathematics, with applications spanning various fields from everyday calculations to complex scientific analyses. This article delves into the interpretation and application of the fraction 35 out of 120, exploring its representation as a percentage, ratio, and demonstrating its practical use in real-world scenarios. We will also explore the mathematical concepts underpinning this fraction and provide a comprehensive guide for understanding similar calculations.
Introduction: Understanding the Basics
The fraction "35 out of 120" represents a part-to-whole relationship. It signifies that 35 units are present out of a total of 120 units. This can be expressed mathematically as 35/120. Understanding this fundamental representation is the first step to exploring its various applications and interpretations. We'll unpack this fraction, explaining how to simplify it, convert it to a percentage, and understand its meaning within different contexts. This knowledge is crucial for various applications, from calculating grades to analyzing statistical data.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before proceeding with further calculations, simplifying the fraction 35/120 is beneficial for easier understanding and manipulation. This involves finding the greatest common divisor (GCD) of both the numerator (35) and the denominator (120). The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- Prime factorization of 35: 5 x 7
- Prime factorization of 120: 2 x 2 x 2 x 3 x 5
The common factor is 5. Dividing both the numerator and the denominator by 5, we get:
35 ÷ 5 = 7 120 ÷ 5 = 24
Therefore, the simplified fraction is 7/24. This simplified form is easier to work with in subsequent calculations and provides a more concise representation of the initial fraction.
2. Converting the Fraction to a Percentage: Understanding Proportions
Converting a fraction to a percentage allows for easier comparison and interpretation, particularly in contexts requiring relative proportions. To convert 7/24 to a percentage, we follow these steps:
- Divide the numerator by the denominator: 7 ÷ 24 ≈ 0.2917
- Multiply the result by 100: 0.2917 x 100 ≈ 29.17%
Therefore, 35 out of 120 is approximately 29.17%. This means that 35 represents approximately 29.17% of the total 120 units. This percentage representation provides a clear and readily understandable measure of the proportion.
3. Representing the Fraction as a Ratio: Expressing Relationships
A ratio expresses the relative size of two or more values. The fraction 35/120, or its simplified form 7/24, can be expressed as a ratio of 7:24. This signifies that for every 7 units of one quantity, there are 24 units of another. This representation is particularly useful when comparing quantities or proportions. For example, if we're discussing the ratio of successful attempts to total attempts, 7:24 indicates that for every 7 successful attempts, there were 24 total attempts.
4. Real-World Applications: Diverse Contexts and Scenarios
The fraction 35/120, and its simplified and percentage forms, find applications in a wide range of real-world scenarios:
-
Academic Performance: Imagine a student answering 35 questions correctly out of a total of 120 questions on an exam. Their score would be 29.17%, indicating their performance relative to the total number of questions. This allows for easy comparison with other students' scores and assessment of their understanding of the subject matter.
-
Sales and Marketing: If a company sells 35 units of a product out of 120 units produced, the sales rate is 29.17%. This data is crucial for analyzing market demand, inventory management, and production planning. Understanding this ratio helps in adjusting production strategies and optimizing sales efforts.
-
Quality Control: In a manufacturing setting, if 35 out of 120 products fail a quality check, the defect rate is 29.17%. This information is essential for identifying production flaws, improving manufacturing processes, and ensuring product quality. Such analysis helps prevent further defects and ensure customer satisfaction.
-
Statistical Analysis: In statistical studies, 35/120 could represent the proportion of individuals exhibiting a particular characteristic within a sample size of 120. This fraction becomes a vital piece of data for analyzing trends, making predictions, and drawing conclusions about the population from which the sample was taken. Proper interpretation of this proportion is key to the validity of the study's findings.
-
Financial Calculations: Financial calculations often involve proportions and percentages. 35/120 might represent a proportion of a portfolio's investment in a specific asset, facilitating analysis of risk and return.
5. Further Mathematical Explorations: Extending the Understanding
The fraction 35/120 offers an opportunity to explore several key mathematical concepts:
-
Decimal Representation: As we saw, 7/24 is approximately 0.2917. Understanding the decimal representation is crucial for calculations involving other numbers and for comparisons using decimal values.
-
Proportionality: The fraction highlights the concept of proportionality, demonstrating the relationship between two quantities. Understanding proportionality is essential in scaling problems, solving equations, and comprehending various mathematical models.
-
Ratio and Proportion: The ratio 7:24 showcases the relationship between two quantities, essential in problem-solving scenarios involving proportions. Mastering the concept of ratio and proportion is fundamental in various mathematical applications.
-
Percentage Calculation: The conversion to 29.17% emphasizes the significance of percentage calculations in expressing proportions in a universally understood format. This skill is essential in many fields, enabling accurate comparisons and interpretations.
6. Frequently Asked Questions (FAQs)
-
Q: How can I calculate the percentage without a calculator?
A: While a calculator simplifies the process, you can perform the division manually. Remember, dividing 7 by 24 will result in a decimal. Multiplying this decimal by 100 gives the percentage. You can round off the result for a practical approximation.
-
Q: Are there other ways to simplify 35/120?
A: The most efficient method is finding the greatest common divisor, which we did using prime factorization. Other methods exist, such as the Euclidean algorithm, but they yield the same simplified fraction of 7/24.
-
Q: What if I have a similar fraction but with larger numbers?
A: The same principles apply. Find the greatest common divisor to simplify the fraction, then divide the numerator by the denominator and multiply by 100 to find the percentage. Larger numbers might require a calculator for efficiency.
-
Q: Is the percentage always exactly 29.17%?
A: No. The calculation resulted in approximately 29.17%. The percentage is an approximation because the decimal representation of 7/24 is non-terminating (it continues infinitely). The level of precision depends on the context and required accuracy.
7. Conclusion: A Foundation for Further Learning
Understanding the fraction 35 out of 120, whether expressed as a simplified fraction (7/24), a percentage (approximately 29.17%), or a ratio (7:24), is a crucial building block in mathematical literacy. The ability to manipulate and interpret these representations is invaluable across various disciplines, facilitating effective problem-solving, data analysis, and decision-making in a multitude of scenarios. This exploration goes beyond a simple calculation; it provides a stepping stone to understanding more complex mathematical concepts and their real-world applications. Mastering these fundamental skills equips you with a powerful toolkit for navigating the quantitative aspects of the world around us. By grasping these concepts, you develop a stronger mathematical foundation for future learning and problem-solving.
Latest Posts
Latest Posts
-
65 Of 40
Sep 12, 2025
-
40 Of 55
Sep 12, 2025
-
63 4kg In Stone
Sep 12, 2025
-
Mpg To Kmpl
Sep 12, 2025
-
20 Of 225
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.