0.75 X 5
stanleys
Sep 15, 2025 · 6 min read
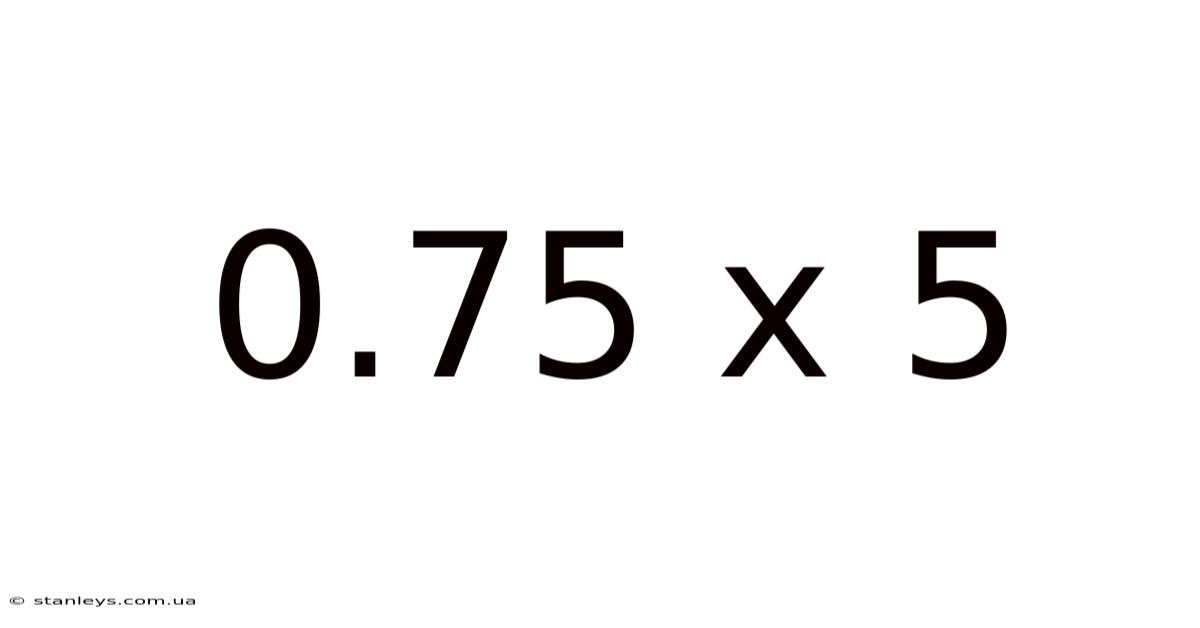
Table of Contents
Unveiling the Simplicity and Power of 0.75 x 5: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 0.75 x 5, delving beyond the immediate answer to uncover the underlying mathematical principles and its diverse applications across various fields. Understanding this seemingly basic calculation provides a foundational understanding of decimal multiplication, fraction conversion, and its practical relevance in everyday life and specialized disciplines. We'll explore different approaches to solving this problem, discuss its real-world implications, and even touch upon related concepts to enhance your overall mathematical comprehension.
Understanding the Basics: Decimals and Fractions
Before we tackle 0.75 x 5, let's refresh our understanding of decimals and fractions. Decimals are a way of writing numbers that are not whole numbers. They use a decimal point to separate the whole number part from the fractional part. For instance, 0.75 represents seventy-five hundredths (75/100).
Fractions, on the other hand, express parts of a whole. They consist of a numerator (top number) and a denominator (bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of parts the whole is divided into. 0.75 can be expressed as the fraction ¾ (three-quarters). Understanding this equivalence is crucial for solving multiplication problems involving decimals.
Calculating 0.75 x 5: Multiple Approaches
There are several ways to calculate 0.75 x 5, each offering a unique perspective and reinforcing different mathematical concepts.
Method 1: Direct Decimal Multiplication
This is the most straightforward approach. Simply multiply 0.75 by 5 using standard multiplication:
0.75
x 5
-------
3.75
Therefore, 0.75 x 5 = 3.75.
Method 2: Fraction Conversion and Multiplication
Converting 0.75 to its fractional equivalent (¾) allows us to use fraction multiplication:
3/4 x 5/1 = (3 x 5) / (4 x 1) = 15/4
To convert the improper fraction 15/4 back to a decimal, we perform the division: 15 ÷ 4 = 3.75. This confirms our previous result. This method emphasizes the equivalence between decimals and fractions and reinforces the rules of fraction multiplication.
Method 3: Distributive Property
The distributive property of multiplication allows us to break down the problem into simpler parts. We can rewrite 0.75 as 0.5 + 0.25:
(0.5 + 0.25) x 5 = (0.5 x 5) + (0.25 x 5) = 2.5 + 1.25 = 3.75
This method demonstrates a valuable algebraic concept and shows how complex calculations can be simplified by breaking them down into smaller, manageable parts.
Method 4: Repeated Addition
Multiplication can be viewed as repeated addition. 0.75 x 5 is equivalent to adding 0.75 five times:
0.75 + 0.75 + 0.75 + 0.75 + 0.75 = 3.75
This approach reinforces the fundamental relationship between addition and multiplication, especially helpful for visualizing the calculation, particularly for learners who are still developing their understanding of multiplication.
Real-World Applications of 0.75 x 5 and Related Calculations
The seemingly simple calculation of 0.75 x 5 has surprisingly widespread applications in various fields:
-
Everyday Finances: Imagine buying five items that cost $0.75 each. The total cost would be 0.75 x 5 = $3.75. This simple calculation is vital for managing personal budgets and making informed purchasing decisions. Similar calculations are used extensively in calculating sales tax, discounts, and unit pricing.
-
Measurement and Conversion: If you're working with measurements (e.g., length, weight, volume), you might encounter scenarios requiring calculations involving decimals and fractions. For example, if you have five pieces of wood, each measuring 0.75 meters, the total length would be 3.75 meters. This is relevant in construction, engineering, and various other fields involving precise measurements.
-
Baking and Cooking: Recipes often involve fractional measurements. If a recipe calls for ¾ cups of flour per serving and you're making five servings, you'd need 0.75 x 5 = 3.75 cups of flour. Accurate calculations are crucial for achieving the desired consistency and taste in cooking and baking.
-
Data Analysis and Statistics: Calculations involving decimals and fractions are ubiquitous in data analysis and statistics. Calculating averages, percentages, and other statistical measures often involve multiplying decimals and fractions. This is applicable in various fields, including research, finance, and market analysis.
-
Engineering and Design: Engineers and designers frequently encounter calculations involving fractions and decimals when working with blueprints, specifications, and measurements. Precise calculations are crucial to ensure structural integrity and functionality in engineering projects.
-
Scientific Calculations: Many scientific calculations, especially in chemistry and physics, involve precise measurements and calculations that frequently utilize decimals and fractions.
Expanding the Knowledge: Related Mathematical Concepts
Understanding 0.75 x 5 opens the door to exploring several related mathematical concepts:
-
Percentage Calculations: Since 0.75 is equivalent to 75%, this calculation can be framed as finding 75% of 5. This connects decimal multiplication to percentage calculations, a vital skill in various contexts.
-
Proportions and Ratios: The problem can be viewed as a proportion: ¾ is to 1 as x is to 5. Solving this proportion reinforces understanding of proportional reasoning.
-
Algebraic Equations: The calculation can be represented algebraically as 0.75x = 3.75, where solving for x involves applying inverse operations. This introduces an element of algebraic thinking.
-
Advanced Mathematical Applications: The principles underlying this simple calculation extend to more complex mathematical operations, including calculus and linear algebra, demonstrating the foundational nature of this seemingly basic concept.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve 0.75 x 5? A: Absolutely! Calculators are efficient tools for performing such calculations, especially for more complex problems.
-
Q: Why are there multiple ways to solve this problem? A: Different methods highlight various mathematical concepts and principles, catering to different learning styles and deepening understanding.
-
Q: Is it always necessary to convert decimals to fractions? A: No, direct decimal multiplication is often the quickest and most efficient method. Fraction conversion is beneficial for reinforcing fundamental concepts and demonstrating equivalencies.
-
Q: What if the numbers were larger or involved more decimal places? A: The same principles apply, but the calculations might become more complex. Calculators become increasingly helpful in such scenarios.
-
Q: How does this relate to other areas of mathematics? A: The concepts of decimals, fractions, multiplication, and the distributive property are fundamental building blocks for more advanced mathematical concepts.
Conclusion: The Significance of Simplicity
While the calculation of 0.75 x 5 might appear trivial at first glance, it serves as a powerful illustration of fundamental mathematical concepts and their wide-ranging applications. By exploring different approaches and considering its real-world relevance, we uncover the depth and significance of seemingly simple mathematical operations. Understanding this basic calculation not only enhances mathematical skills but also fosters a deeper appreciation for the power and utility of mathematics in everyday life and specialized fields. The simplicity of this equation belies its importance as a building block for more complex mathematical understanding and practical problem-solving. Mastering this foundational concept lays a strong groundwork for tackling more challenging mathematical endeavors in the future.
Latest Posts
Latest Posts
-
Tbsp To Ounces
Sep 15, 2025
-
Staff In Training
Sep 15, 2025
-
45cm To M
Sep 15, 2025
-
10 M L
Sep 15, 2025
-
6th Square Number
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 0.75 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.