3 X 9
stanleys
Sep 14, 2025 · 6 min read
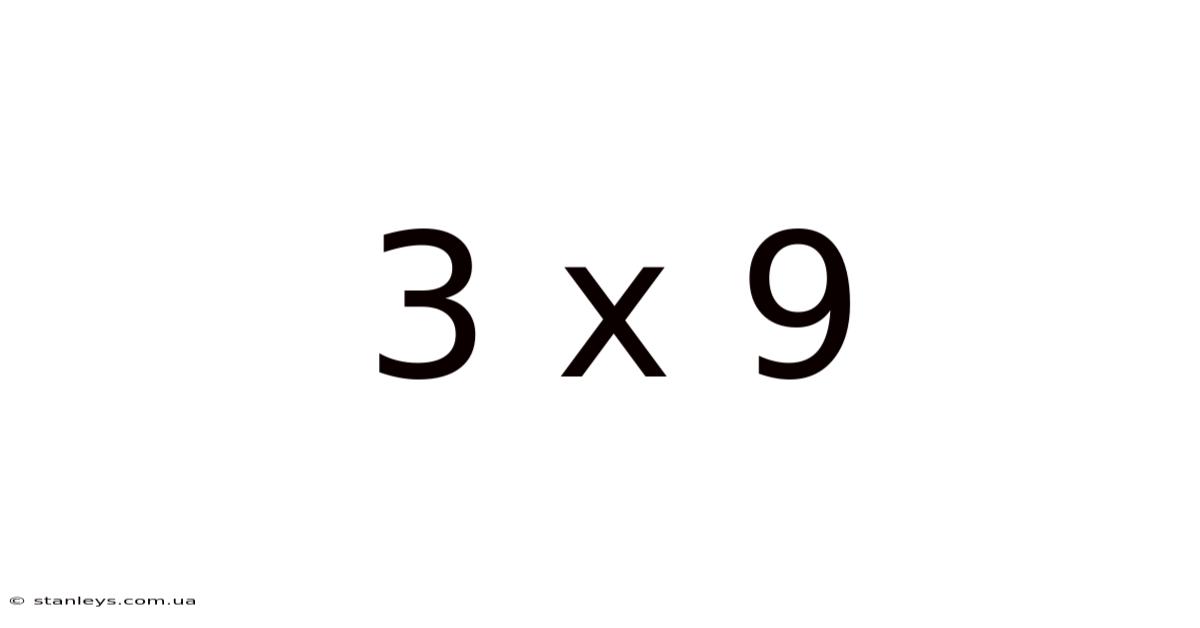
Table of Contents
Exploring the Mathematical Landscape of 3 x 9: From Basic Multiplication to Advanced Applications
The seemingly simple equation, 3 x 9, serves as a gateway to understanding a vast range of mathematical concepts. While the answer – 27 – is readily apparent to most, delving deeper reveals its significance within the broader context of multiplication, number theory, and even real-world applications. This article will explore 3 x 9 from its foundational arithmetic principles to its more advanced implications, offering insights for students, educators, and anyone curious about the hidden depths of seemingly simple numbers.
I. Understanding the Fundamentals: Multiplication and its Properties
At its core, 3 x 9 represents multiplication, a fundamental arithmetic operation. Multiplication can be viewed in several ways:
-
Repeated Addition: 3 x 9 is equivalent to adding three nine times: 9 + 9 + 9 = 27. This is a foundational understanding, especially helpful for younger learners.
-
Array Representation: Imagine a rectangular array with three rows and nine columns. The total number of elements in this array (3 x 9) represents the product. This visual representation helps solidify the concept of multiplication.
-
Commutative Property: Multiplication is commutative, meaning the order of the operands doesn't affect the result. Therefore, 3 x 9 is equal to 9 x 3. This property offers flexibility in calculations and problem-solving.
-
Associative Property: When multiplying more than two numbers, the associative property allows us to group them differently without altering the outcome. For instance, (3 x 3) x 3 = 3 x (3 x 3) = 27. This property is vital for simplifying complex calculations.
-
Distributive Property: This property links multiplication and addition. It states that a(b + c) = ab + ac. For example, 3 x (10 - 1) = (3 x 10) - (3 x 1) = 30 - 3 = 27. This property is extremely useful in simplifying calculations involving larger numbers.
II. Exploring 3 x 9 within Number Theory
Beyond its basic arithmetic application, 3 x 9 offers intriguing insights within number theory:
-
Factors and Multiples: The numbers 3 and 9 are factors of 27, while 27 is a multiple of both 3 and 9. Understanding factors and multiples is crucial for simplifying fractions, finding common denominators, and working with prime factorization.
-
Prime Factorization: 27 can be expressed as its prime factorization: 3 x 3 x 3 or 3³. Prime factorization is a cornerstone of number theory with applications in cryptography and other advanced mathematical fields.
-
Divisibility Rules: 27 is divisible by 3 and 9. This is in line with divisibility rules: a number is divisible by 3 if the sum of its digits is divisible by 3 (2 + 7 = 9, which is divisible by 3); and a number is divisible by 9 if the sum of its digits is divisible by 9.
-
Perfect Number Relationships: While 27 isn’t a perfect number (a number equal to the sum of its proper divisors), exploring its divisors (1, 3, 9, 27) helps illustrate concepts related to perfect numbers and their properties.
-
Modular Arithmetic: In modular arithmetic, we consider the remainder after division. For example, 27 mod 3 = 0 and 27 mod 9 = 0. This system is fundamental to cryptography and computer science.
III. Real-World Applications of 3 x 9 and Related Concepts
The seemingly simple equation 3 x 9 finds its way into various real-world scenarios:
-
Everyday Counting: Imagine arranging items in rows and columns. If you have three rows of nine items each, you have a total of 27 items. This simple application underscores the practicality of multiplication in daily life.
-
Geometry: Calculating the area of a rectangle with dimensions 3 units by 9 units involves using 3 x 9 to arrive at an area of 27 square units. This concept extends to more complex geometric calculations.
-
Measurement and Conversion: Imagine converting units. If a box has 3 layers with 9 items per layer, the total number of items is 27. This extends to unit conversions in various fields.
-
Finance: Calculating the cost of three items priced at $9 each uses 3 x 9 to find the total cost of $27. This elementary calculation is fundamental in personal finance and business.
-
Data Analysis: In data analysis, encountering a 3 x 9 data matrix is common. Understanding the dimensions is crucial for data interpretation and analysis.
IV. Expanding the Horizons: Advanced Mathematical Connections
The simple equation 3 x 9 opens doors to more advanced mathematical concepts:
-
Algebra: The expression 3x = 27 is an algebraic equation where 'x' represents 9. Solving such equations forms the basis of algebra and its various applications.
-
Calculus: While not directly involved, the principles of multiplication and number theory underpin many concepts in calculus, particularly those related to limits, derivatives, and integrals.
-
Linear Algebra: Matrices and vectors, fundamental components of linear algebra, often involve multiplications similar to 3 x 9. Understanding such operations is essential in various scientific and engineering applications.
-
Number Systems: 3 x 9 can be explored in different number systems like binary, hexadecimal, or other bases. This opens up broader perspectives on numerical representations.
V. Addressing Common Questions and Misconceptions (FAQ)
Q: Is there a quicker way to calculate 3 x 9 than simple multiplication?
A: While standard multiplication is efficient, some might find using the distributive property helpful: 3 x (10 - 1) = 30 - 3 = 27. Others might memorize the multiplication table.
Q: What are some common errors students make when calculating 3 x 9?
A: Common errors include misremembering the multiplication fact or errors in addition when using repeated addition. Clear understanding of the multiplication concept is key to avoiding these errors.
Q: How can I make learning 3 x 9 and other multiplication facts more engaging for children?
A: Use visual aids, like arrays or objects, to represent the multiplication. Games, interactive apps, and real-world examples can also enhance engagement.
Q: Are there any patterns or tricks to quickly remember the multiplication table involving 9?
A: Yes! Notice that the digits of the products of 9 always add up to 9 (9 x 1 = 9, 9 x 2 = 18, 1+8 = 9, 9 x 3 = 27, 2+7 =9, and so on). This pattern can aid memorization. Also, the tens digit increases by one while the ones digit decreases by one as you go through the multiples of nine.
VI. Conclusion: The Unfolding Story of 3 x 9
The seemingly simple equation 3 x 9, resulting in 27, reveals a surprisingly rich mathematical landscape. From its basic arithmetic functions to its advanced applications in number theory, algebra, and various other mathematical fields, it illustrates the interconnectedness of mathematical concepts. Understanding 3 x 9 and the principles it embodies is not merely about memorizing a single multiplication fact; it's about developing a deeper appreciation for the beauty and elegance of mathematics and its pervasive presence in our world. By exploring this simple equation, we unlock a gateway to understanding a broader mathematical universe, demonstrating the power of even the most fundamental mathematical concepts. This exploration encourages a deeper understanding of the building blocks of mathematics and its profound real-world applications. The journey from the simple act of multiplication to the complex world of mathematical theory highlights the ever-expanding possibilities inherent in the seemingly simple equation: 3 x 9 = 27.
Latest Posts
Latest Posts
-
112 4kg In Stone
Sep 14, 2025
-
36 6celsius To Fahrenheit
Sep 14, 2025
-
Humanism And Secularism
Sep 14, 2025
-
Multiple Employer Trust
Sep 14, 2025
-
40 Cm M
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 X 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.