3 X 4/15
stanleys
Sep 17, 2025 · 5 min read
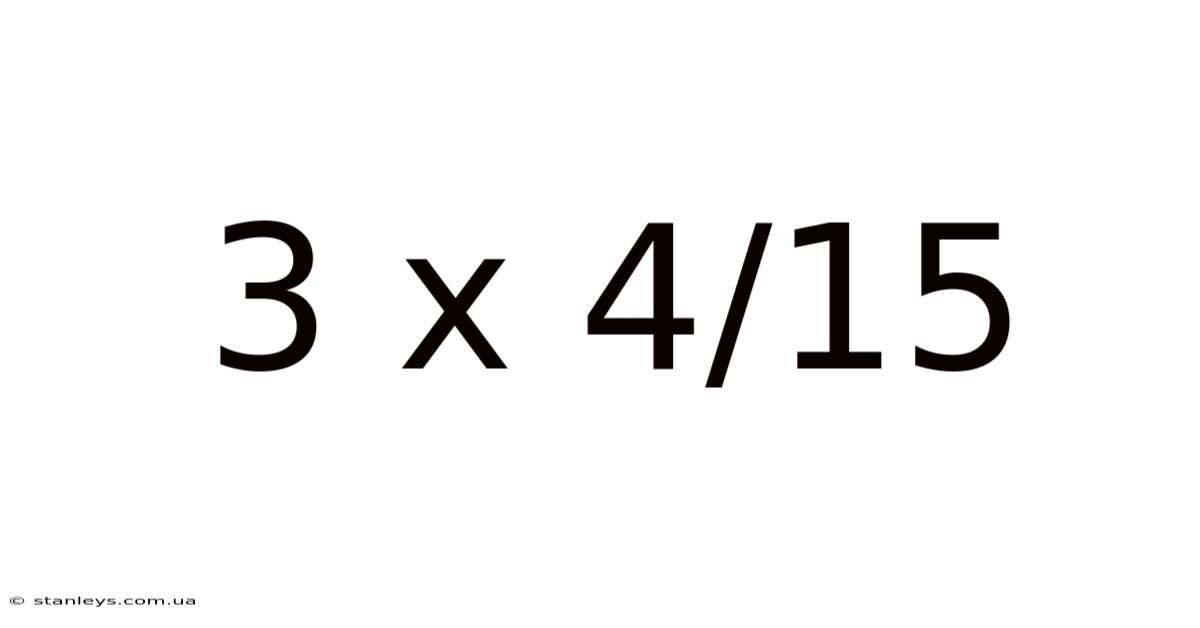
Table of Contents
Unveiling the Mysteries of 3 x 4/15: A Deep Dive into Fractions and Multiplication
This article will explore the seemingly simple mathematical expression "3 x 4/15," delving into the fundamental principles of fraction multiplication and providing a comprehensive understanding of how to solve it. We'll move beyond a simple numerical answer to explore the underlying concepts, offering practical examples and addressing common misconceptions. Understanding this seemingly straightforward calculation unlocks a deeper appreciation for fractional arithmetic and its applications in various fields.
Understanding the Components: Fractions and Multiplication
Before tackling the problem, let's refresh our understanding of the key components: fractions and multiplication.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, 4/15 means 4 out of 15 equal parts.
-
Multiplication: In the context of fractions, multiplication signifies finding a specific portion of a quantity. Multiplying a whole number by a fraction means finding that fractional part of the whole number. Multiplying two fractions involves finding a portion of a portion.
Step-by-Step Solution: 3 x 4/15
Now, let's break down the solution to 3 x 4/15 step-by-step:
Step 1: Rewrite the Whole Number as a Fraction
To simplify the multiplication process, it's helpful to express the whole number (3) as a fraction. Any whole number can be written as a fraction with a denominator of 1. Therefore, 3 can be rewritten as 3/1.
Our expression now becomes: (3/1) x (4/15)
Step 2: Multiply the Numerators and the Denominators
The next step involves multiplying the numerators together and the denominators together separately.
- Numerator multiplication: 3 x 4 = 12
- Denominator multiplication: 1 x 15 = 15
This gives us the result: 12/15
Step 3: Simplify the Fraction (Reduce to Lowest Terms)
The fraction 12/15 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (12) and the denominator (15). The GCD is the largest number that divides both 12 and 15 without leaving a remainder. In this case, the GCD is 3.
We divide both the numerator and the denominator by the GCD:
- 12 ÷ 3 = 4
- 15 ÷ 3 = 5
This simplifies the fraction to its lowest terms: 4/5
Therefore, 3 x 4/15 = 4/5
A Deeper Look: The Commutative Property and Simplification Strategies
The commutative property of multiplication states that the order of the factors does not affect the product. This means that 3 x (4/15) is equivalent to (4/15) x 3. Understanding this property allows for flexible approaches to solving similar problems.
Furthermore, we could have simplified the expression before multiplying. Notice that we can cancel common factors between the numerator and denominator before performing the multiplication. This is often called "cross-cancellation" or simplifying before multiplying.
Observe the original expression: (3/1) x (4/15)
Notice that 3 (in the numerator) and 15 (in the denominator) share a common factor of 3. We can divide both by 3:
(3 ÷ 3) / (15 ÷ 3) = 1/5
Now our expression becomes: (1/1) x (4/5) = 4/5
This method simplifies the calculation and avoids the need to simplify the final fraction. It demonstrates the efficiency of simplifying before multiplying.
Practical Applications and Real-World Examples
Understanding fraction multiplication is crucial in numerous real-world scenarios:
-
Baking: A recipe calls for 2/3 cups of flour, and you want to triple the recipe. You need to calculate 3 x (2/3), which equals 2 cups of flour.
-
Construction: Calculating the amount of materials needed for a project often involves fractions. If a task requires 3/4 of a bag of cement, and you need to complete 5 such tasks, you would calculate 5 x (3/4) to determine the total amount of cement needed.
-
Finance: Calculating interest, discounts, or portions of investments frequently involves fraction multiplication.
-
Data Analysis: Many statistical analyses involve calculations with fractions and percentages, which are essentially fractions expressed as a proportion of 100.
Common Misconceptions and Pitfalls
Several common misconceptions can lead to incorrect answers when working with fractions:
-
Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS). If there are other operations involved (parentheses, exponents, etc.), perform them before multiplication.
-
Forgetting to simplify: Always simplify the resulting fraction to its lowest terms to ensure the answer is expressed in the most concise and accurate form.
-
Incorrect cancellation: When simplifying before multiplying, ensure you're canceling common factors from the numerator and denominator of different fractions. You cannot cancel common factors within the same fraction's numerator and denominator.
Frequently Asked Questions (FAQ)
Q: Can I multiply the whole number by the numerator only?
A: No. You must treat the whole number as a fraction (with a denominator of 1) and multiply both the numerators and the denominators.
Q: What if the fraction is an improper fraction (numerator is larger than the denominator)?
A: The process remains the same. Multiply the numerators and the denominators, then simplify the resulting fraction. You may end up with an improper fraction or a mixed number (whole number and a fraction).
Q: Is there a way to solve this using decimals instead of fractions?
A: Yes. You can convert the fraction 4/15 to a decimal (approximately 0.2667) and then multiply by 3. However, working directly with fractions often provides a more precise answer and avoids rounding errors.
Q: How can I improve my skills in fraction multiplication?
A: Practice is key. Work through various problems, focusing on different types of fractions (proper, improper, mixed numbers). Also, understand the underlying concepts thoroughly, particularly the commutative property and the simplification strategies.
Conclusion: Mastering the Fundamentals of Fraction Multiplication
Understanding 3 x 4/15 extends far beyond a simple numerical answer. It's about grasping the fundamental principles of fraction multiplication, the power of simplification techniques, and appreciating the practical applications of these concepts in various fields. By mastering these concepts, you'll build a solid foundation in mathematics, empowering you to tackle more complex calculations with confidence and accuracy. Remember to practice regularly and utilize different approaches to solidify your understanding. With continued effort, you'll find that solving fraction problems becomes increasingly intuitive and straightforward.
Latest Posts
Latest Posts
-
28 Times 5
Sep 17, 2025
-
24 Of 75
Sep 17, 2025
-
3 Dl Ml
Sep 17, 2025
-
Hard To Beat
Sep 17, 2025
-
10 Off 140
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 X 4/15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.